Mesh (surface) Denoising

Meshes obtained from real world objects are often noisy.

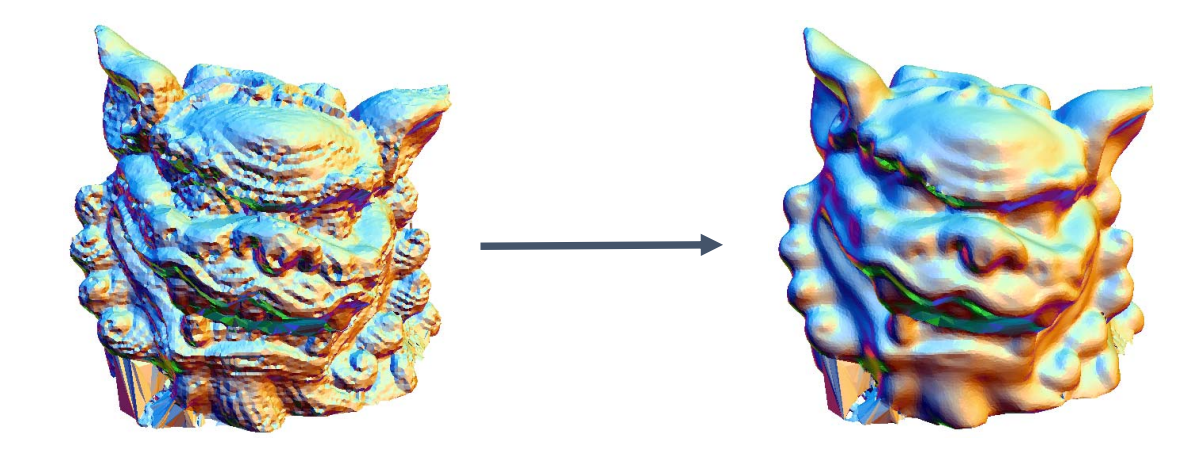
• Mesh denoising
• Mesh smoothing
• Mesh filtering
• Mesh improvement
• Surface fairing (*)

这几个词都是去噪的不同表达。
在连续几何中， fairing 代表光顺，与 smoothing 不同。
在离散几何中， fairing 与 smoothing 通用。

噪声的特点

No Precise Mathematical Definition! 以下是经验上的描述：

• High‐frequent tiny parts
• Small bumps on the surface
• High curvature parts
• High fairing energy parts
• …

👆 实际上，满足以上特点的不一定是噪声，也有可能是特征。

去噪的难点

去噪的难点在于，噪声和特征都是未知的。因此去噪需要识别噪声和特征，要Eliminate high frequency并Preserve global features

Mesh去噪方法论 - Mesh Smoothing Model

假定：网格顶点的数据及连接关系不变
问题转化为：顶点进行适当的扰动或偏移，得到顶点的新位置，使得“噪声”减少！关键是顶点如何偏移？

定义$M$为含噪声的网格曲面，$M^0$为无噪声的网格曲面，for all $v\in M$，认为：

$$v=v^0+\varepsilon n$$

即顶点偏移的方向为n，大小为$\varepsilon$

好的算法不追求绝对的真实，而是合理的假设与必要的简化

偏移的方向n

n可以是$𝒗^0$点的法向，或$𝒗$点的法向。
如果取前者，仍然是ill‐posed问题。
因此在这里用后者，即v点的法向。

$v是带噪声曲面上的点，v_0$是无噪声曲面上的点。
假设：
① $v是v_0$沿几方向上做了一点偏移。
② $n是v_0$的法方向。
③ 当$v接近v_0$时， $v 的法线方向接近 n$
因此随着逐步迭代，后者会趋进前者。

偏移的大小$\varepsilon$

经验值，不展开

Filtering

连续形式：

$$(x*h)(t)=\int_{-\infty }^{\infty } x(\tau )h(t-\tau )d\tau$$

离散形式：

$$(x*h)(t)= {\textstyle \sum_{𝜏=-\infty }^{\infty }} x(𝜏 )h(t-𝜏 )$$

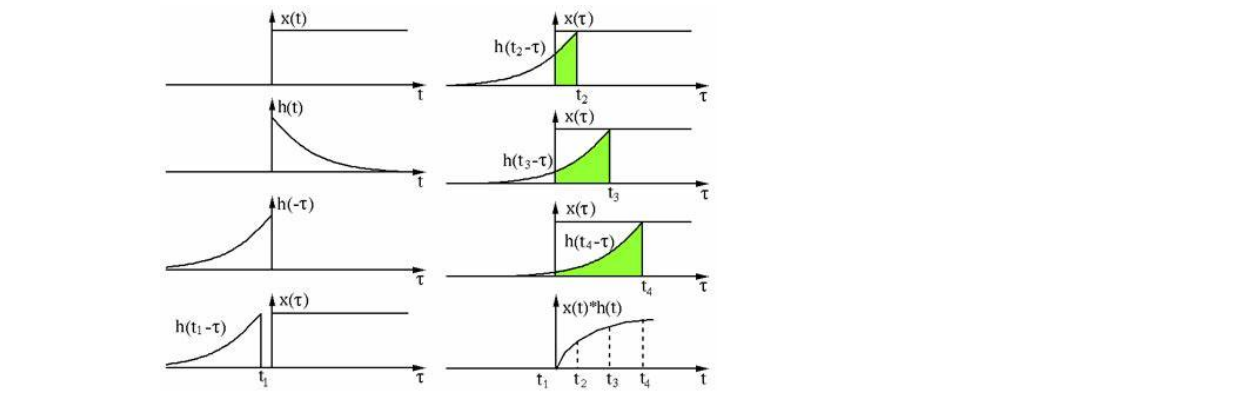
几何意义：
将函数$ℎ(𝑡)$作为权来对$𝑥(𝑡)$进行加权平均（滤波）
将$𝑥(𝑡)$的局部信息进行混合平均

Gaussian Filtering

通常使用Gauss函数作为权函数

$${I}' (u)=\sum _{p\in N(u)}e^{\frac{||u-P||^2}{2\sigma ^2} }I(P)$$

Gauss 函数的好处：
① 概率密度函数，积分和为1.
② 具有对称性
③ 与距离相关

Mesh Vertex Filtering

Laplacian operator / Umbrella Operator：link

滤波对象

• Vertex
• Normal
• Curvature
• Color
• Other physical properties (texture, albedo, … )

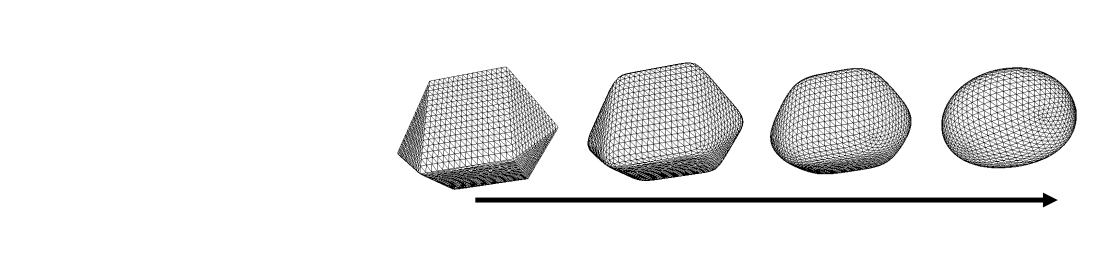
Challenges:

• Iteration number
• Shrinkage

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/