多元函数（多变量）

$$f: R^n \rightarrow R^1$$

$$\begin{pmatrix}x_1 \\\vdots \\x_n \end{pmatrix} \rightarrow y$$

$$y = f(x_1,x_2, \cdots, x_n)$$

例子：通过升级实现二元函数的可视化 $$z=f(x,y),(x,y)\in[0,1]\times[0,1]$$

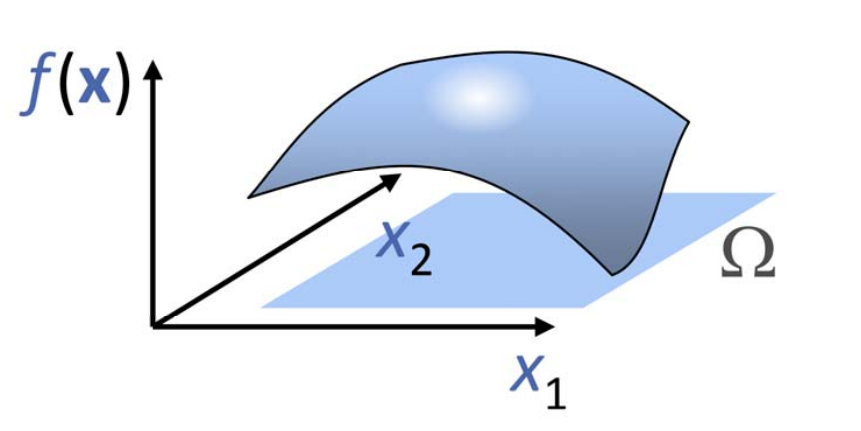
二元函数的基函数构造

张量积，即用两个一元函数的基函数的相互乘积来定义，

例1：二次二元多项式函数$z=f(x,y)$的基函数{$1,x,y,x^2,xy,y^2$}

✅ [10:23] 例子中幂基最高为二次，因此只取不超过二次的项。

例2： 以任意函数为基函数

👆 [11:22] 例子：任意基。横轴和竖轴可以用不同的函数，但很少这样做。

多元函数的基函数构造

多元函数的张量积定义

优点：定义简单，多个一元基函数的乘积形式
不足：随着维数增加，基函数个数急剧增加，导致变量急据增加

求解系统规模急剧增加、求解代价大、占用内存空间大

多元函数的神经网络表达

用一个单变量函数$\sigma (x)$（称为激活函数）的不同仿射变换来构造 “基函数”：基函数数目可控
$$y=f(x_1,x_2,...,x_n)$$ $$=w_0+\sum_{j-1}^{m} w_j\sigma (a_j^1x_1+...a_j^ix_i+...+a_j^nx_n+b_j)$$

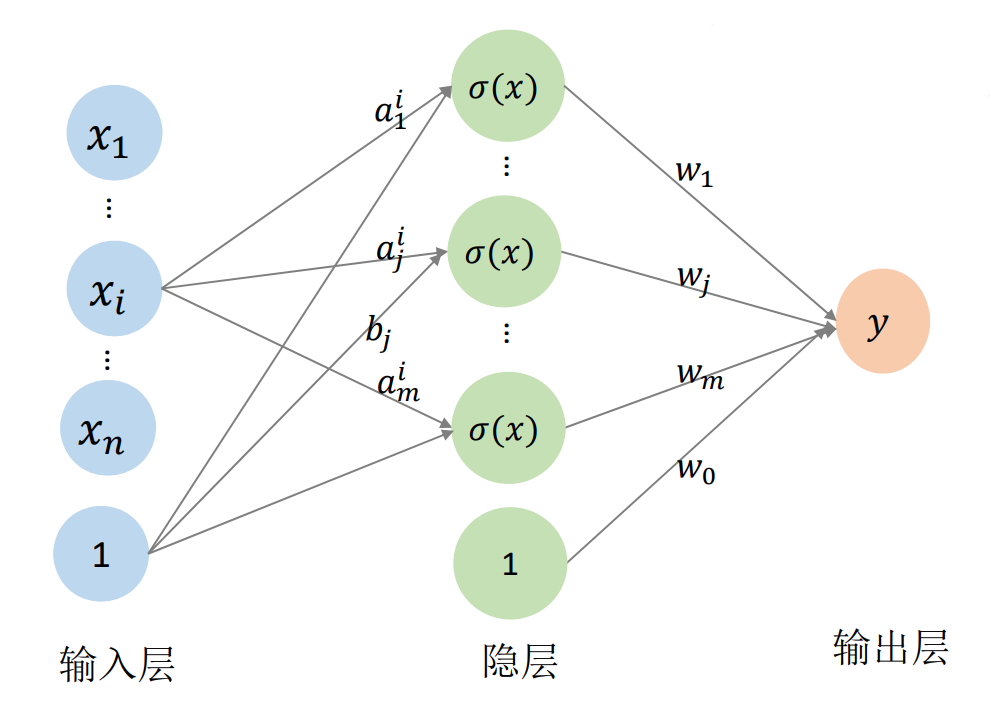
🔎 [16:12]
✅ 神网络方式的优点：
（1）可以解决张量积方式的维数膨胀问题，因为张量积的维度是指数级增长，而神经网络的$m$可以控制。
（2）有统一的优化方法和优化框架
❗ 存在的问题：仍需要调参

💡 我的思考
能用低维的神经网络代替高维的张量积，是因为，虽然张量积的各维­度独立，但它对于要拟合的数据来说是有冗余的。
神经网络 hidden layer 的本质，把$n$维空间的点映射到m维空间的点，网络学习点在不同维度空间中的性质。

本文出自CaterpillarStudyGroup，转载请注明出处。 https://caterpillarstudygroup.github.io/GAMES102_mdbook/