不可形变Mesh与刚体
Mesh由顶点、边、面片组成。
不可形变的Mesh指，Mesh上的顶点、边、面片的相对位置位移保持不变，因此把不可形变Mesh称为刚体。刚体的特点是物体很硬，不考虑形变。
Mesh由点、线、面组成，从不同的角度看待Mesh，可以得到不同的仿真属性和仿真方法，用于不同的仿真目的。
刚体的仿真属性
把Mesh看作一个整体，Mesh相当于一个有体积的粒子。那么Mesh有以下属性：
| 属性 | 符号 | 在通常的仿真场景中是否可变 |
|---|---|---|
| 质量 | m（均质）或M（非均质） | 否。 |
| 全局位置（世界坐标系） | p或x | 是。刚体所占的是一个连续的空间，而不是一个点。选择刚体中的某一个点（通常是质心）的位置作为刚体的位置。 |
| 全局旋转（世界坐标系） | q 旋转的表示戳这里link。最后结论是四元数表示方法。 | 是 |
对应的：
| 属性 | 符号 | 说明 |
|---|---|---|
| 速度 | v或\(\mathbf{\dot{x}} \) | p的一阶导 |
| 加速度 | a | p的二阶导 |
| 角速度 | \(\mathbf{\omega}\)或\(\mathbf{\dot{q}} \) | q的一阶导 |
| 角加速度 | q的二阶导 |
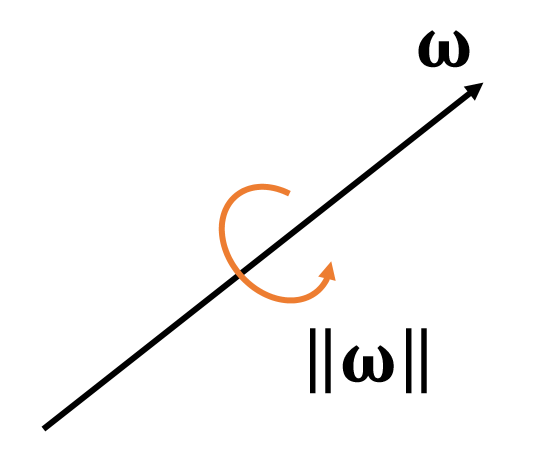
$$
\begin{cases} \text{The direction of } \mathbf{\omega} \text{ is the axis.} \\
\text{The magnitude of } \mathbf{\omega} \text{ is the speed.}
\end{cases}
$$
刚体顶点的属性
刚体上的顶点没有自己的自由度，因此没有仿真属性。但它们具有以下运动属性：
| 属性 | 符号 | 在通常的仿真场景中是否可变 |
|---|---|---|
| 质量 | m | 否 |
| 相对位置(质心的坐标系) | p或x | 否。虽然每个粒子都有位置属性，但它们所有的粒子相对位移不变，因此不需要独立对每个粒子的位置属性做仿真，只需要仿真其中一个粒子的位置就可以。其它粒子的位置都是相对它的偏移 |
| 全局位置（世界坐标系） | \(x_i\) | 是。粒子的位置变化是由于质心坐标的平移和旋转导致的，是被动变化的，因此不直接仿真每个粒子的全局位置。 |
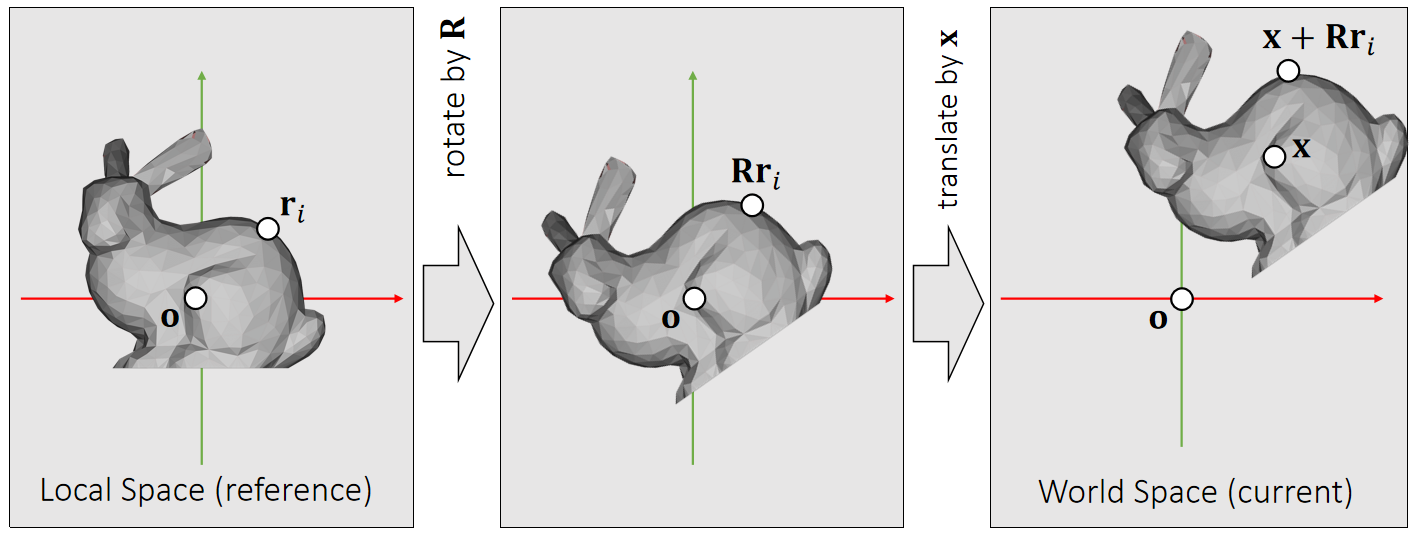
✅ reference：参考状态,无平移,无旋转，假设刚体在reference状态的坐标系与世界坐标系是一致的。
当前状态：旋转为\(\mathbf{R}\)，平移为\(\mathbf{T}\). 那么物体上任意点的位置为：
$$ \mathbf{{x}}' = \mathbf{Rx} + \mathbf{T} $$
粒子视角可以用于Mesh的受力分析，但是不能直接对Mesh上的粒子进行仿真，要把粒子受到的力转化为刚体的受力响应。