P42

Basic Concepts

If $f(\mathbf{x} )\in \mathbf{R} $, then $df=\frac{∂f}{∂x}dx+\frac{∂f}{∂y}dy+\frac{∂f}{∂z}dz=\begin{bmatrix} \frac{∂f}{∂x} & \frac{∂f}{∂y} &\frac{∂f}{∂z} \end{bmatrix}\begin{bmatrix} dx \\ dy\\ dz \end{bmatrix}$.

$$ \frac{∂f}{∂x}=\begin{bmatrix} \frac{∂f}{∂x} & \frac{∂f}{∂y} &\frac{∂f}{∂z} \end{bmatrix}
$$

$$ \mathrm{ or } $$

$\nabla f(\mathbf{x} )=\begin{bmatrix}\frac{∂f}{∂x} \\ \frac{∂f}{∂y}\\\frac{∂f}{∂z}\end{bmatrix}$ gradient

✅ $\nabla f(x)=(\frac{\partial f}{\partial x} )^T$, 重要！！！

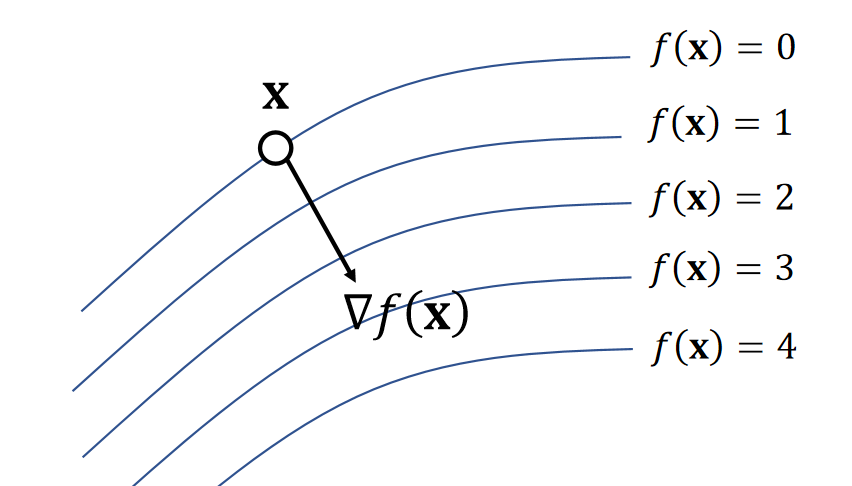
Gradient is the steepest direction for increasing $f$. It’s perpendicular to the isosurface.

✅ isosurface：等高面

P43

值是矢量，变量是是矢量

If $f(\mathbf{x} )=\begin{bmatrix} f(\mathbf{x} ) \\ g(\mathbf{x} )\\ h(\mathbf{x} ) \end{bmatrix}\in \mathbf{R} ^3$,then:

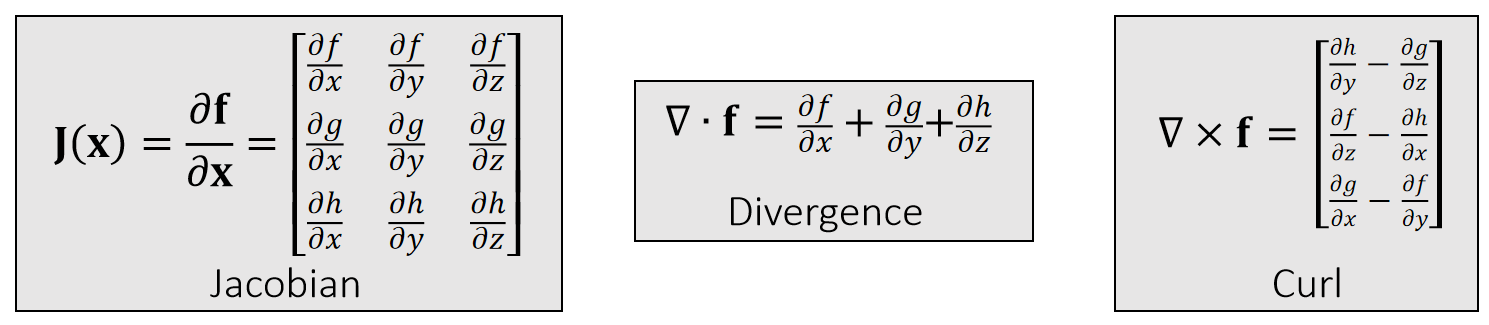
✅ Divergence:散度，也是$\mathbf{J}(\mathbf{x})$的 trace
✅ Curl：旋度。
怎么理解 curl?把微分算子$\nabla $看作是个向量，让它与 $\mathbf{f}$ 做叉乘、在流体模拟中常用。

P44

2nd-Order Derivatives

If $f\mathbf{(x)\in R} $,then:

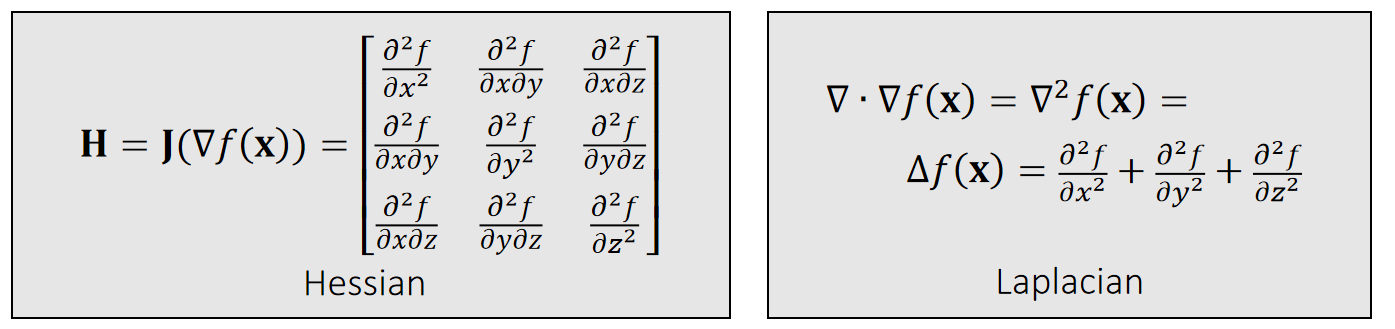
✅ 求导顺序不影响求导结果，因此 $\mathbf{H}$ 是对称的
$\mathbf{H}$的trace称为Laplace

泰勒展开

①$x\in R,f(x)\in R$
$$ f(x)=f(x_0)+{f}' (x_0)(x-x_0)+\frac{1}{2} {f}'' (x_0)(x-x_0)^2+\cdots $$

②$x\in R^n,f(x)\in R$

$$ f(x)=f(x_0)+\rhd {f}' (x_0)\cdot (x-x_0)+\frac{1}{2}(x-x_0)^TH(x-x_0)+\cdots $$

✅ 当$\mathbf{H}$正定时, $f(\mathbf{x})$满足一些特殊的性质

P45

Quiz:

$\frac{∂||\mathbf{x}||}{∂\mathbf{x}} = ?$

$$ \frac{∂||\mathbf{x}||}{∂\mathbf{x} } = \frac{∂(\mathbf{\mathbf{x^Tx} } )^{1/2}}{∂\mathbf{x} }=\frac{1}{2}(\mathbf{x^{T}x} )^{−1/2} \frac{∂(\mathbf{x^Tx} )}{∂\mathbf{x} }=\frac{1}{2||\mathbf{x} ||}2\mathbf{x^T} =\frac{\mathbf{x^T} }{||\mathbf{x} ||} $$