P3
Topics for the Day
-
Hessian of Elastic Energy
-
Implicit Integration
-
Nonlinear optimization.
✅ 隐式积分不讲了。推荐P12页的论文
直接跳到 P18、非线性优化。
P4
Hessian of Elastic Energy
P5
Recall that…
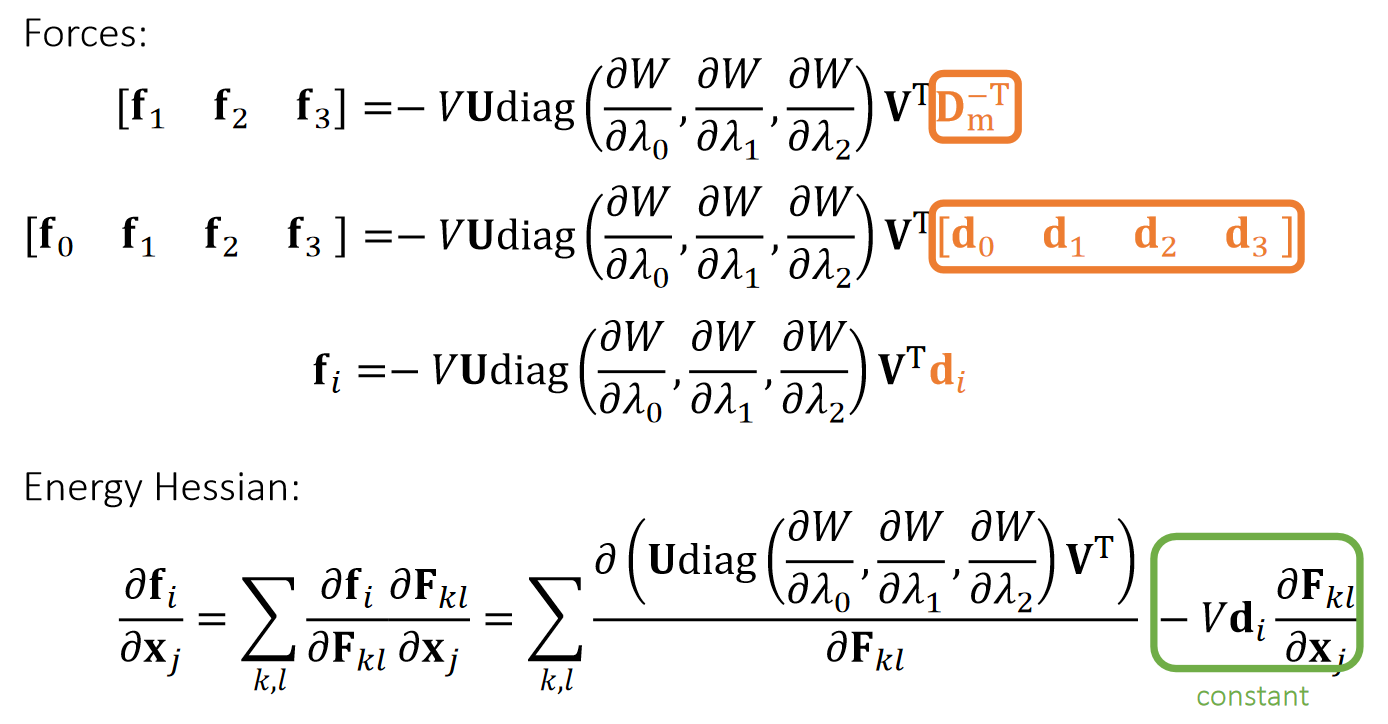
P6
Energy Hessian:
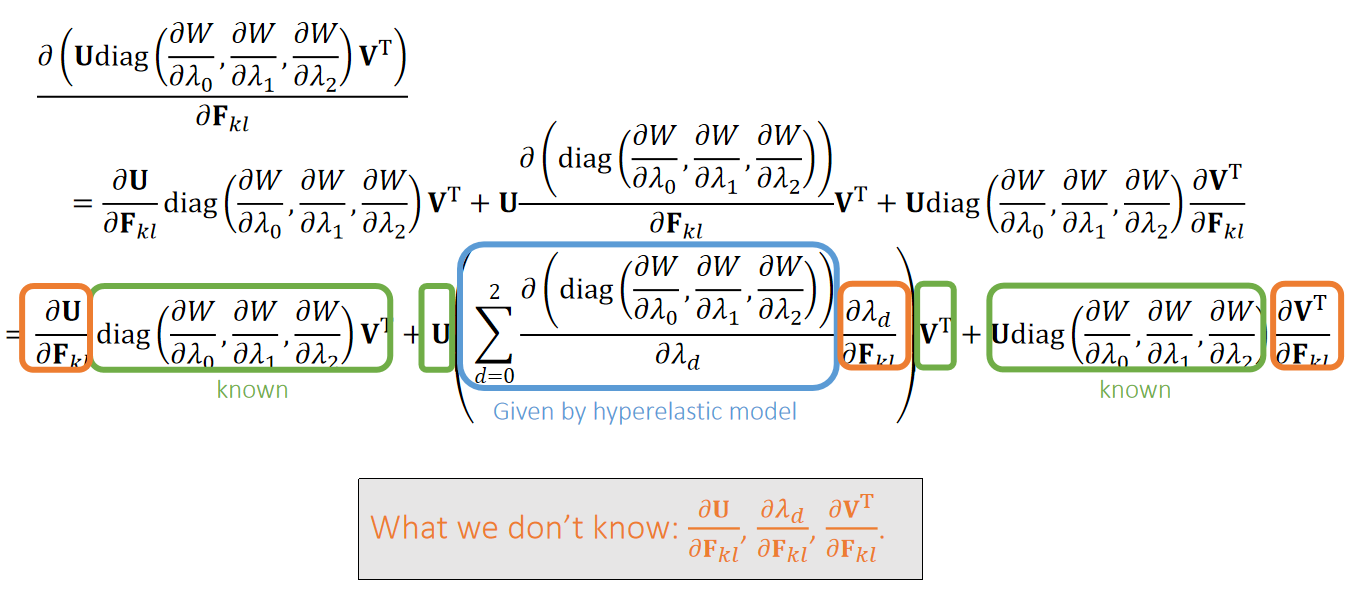
P7
SVD Derivative
Since F=UΛVTis singular value decomposition (Λ=diag(λ0,λ1,λ2)), we can do:
UT∂F∂FklV=UT(∂U∂FklΛVT+U∂Λ∂FklVT+UΛ∂VT∂Fkl)V
UT∂F∂FklV=(UT∂U∂Fkl)Λ+∂Λ∂Fkl+Λ(∂VT∂FklV)
UT∂F∂FklV=AΛ+∂Λ∂Fkl+ΛB
P8
Skew-Symmetric Matrix
Matrix A is skew-symmetric (or anti-symmetric), if A=−AT:
A=[0ab−a0c−b−c0]
If D is diagonal, then:
AD=[0ab−a0c−b−c0][d000e000f]=[0???0???0]
DA=[d000e000f][0ab−a0c−b−c0]=[0???0???0]
When U is orthogonal, we have:
0=∂(UTU)∂Fkl=UT∂U∂Fkl+∂UT∂FklU=UT∂U∂Fkl+(UT∂U∂Fkl)T
Therefore, A=UT∂U∂Fkl is skew-symmetric. So is B=∂VT∂FklV.
P9
SVD Derivative (cont.)
Since F=UΛVT is singular value decomposition Λ=diag(λ0,λ1,λ2), we can do:
UT∂F∂FklV=AΛ+∂Λ∂Fkl+ΛB
After expansion, we get:
UT∂F∂FklV=[0a0a1−a00a2−a1−a20][λ0◻◻◻λ1◻◻◻λ2][∂λ0∂Fkl◻◻◻∂λ1∂Fkl◻◻◻∂λ2∂Fkl][λ0◻◻◻λ1◻◻◻λ2][0b0b1−b00b2−b1−b20]
P10
SVD Derivative (cont.)
Since F=UΛVT is singular value decomposition Λ=diag(λ0,λ1,λ2), we can do:
UT∂F∂FklV=AΛ+∂Λ∂Fkl+ΛB
After expansion, we get:
UT∂F∂FklV=[∂λ0/∂Fklλ1a0+λ0b0λ2a1+λ0b1−λ0a0−λ1b0∂λ1/∂Fklλ2a2+λ1b2−λ0a1−λ2b1−λ1a0a2−λ2b2∂λ2/∂Fkl]
[m00m01m02m10m11m12m20m21m22]=[∂λ0/∂Fklλ1a0+λ0b0λ2a1+λ0b1−λ0a0−λ1b0∂λ1/∂Fklλ2a2+λ1b2−λ0a1−λ2b1−λ1a0a2−λ2b2∂λ2/∂Fkl]
Eventually, we get: A=UT∂U∂Fkl,B=∂VT∂FklV and ∂λ0/∂Fkl,∂λ1/∂Fkl,∂λ2/∂Fkl.
P11
A Quick Summary
- Step 1: By SVD derivatives, we get: ∂U∂Fkl,∂λd∂Fkl,∂VT∂Fkl.
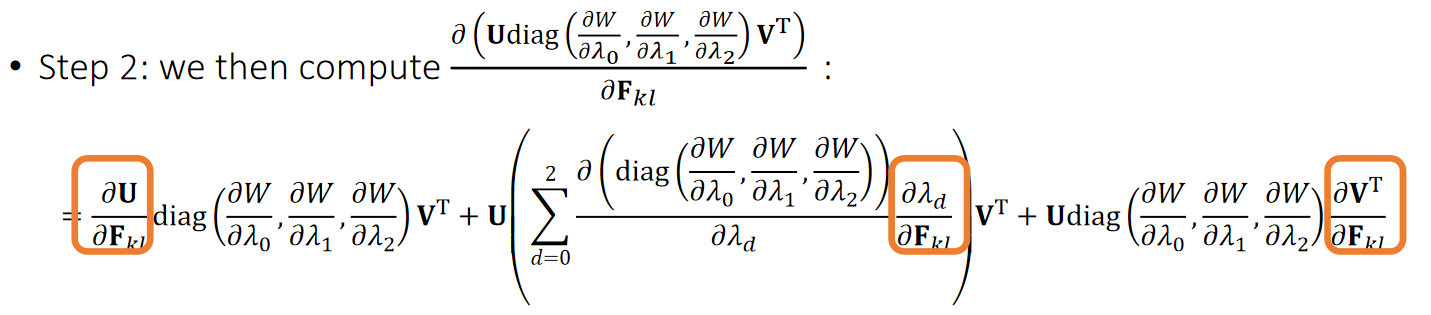
- Step 3: Finally, we reach our goal in Hessian matrix:
∂fi∂xj=∑k,l∂fi∂Fkl∂Fkl∂xj=∑k,l∂(Udiag(∂W∂λ0,∂W∂λ1,∂W∂λ2)VT)∂Fkl−Vdi∂Fkl∂xj
P12
After-Class Reading
Xu et al. 2015. Nonlinear Material Design Using Principal Stretches. TOG (SIGGRAPH).
Definitely read this paper if you decide to implement it.
P13
Implicit Integration
P14
Implicit Integration
Recall that we need implicit integration to avoid numerical instability (Class 5, page 13):
{v[1]=v[0]+∆tM−1f[1]x[1]=x[0]+∆tv[1]
or
{x[1]=x[0]+∆tv[0]+∆t2M−1f[1]v[1]=(x[1]−x[0])/∆t
We also said that:
x[1]=x[0]+∆tv[0]+∆t2M−1f(x[1])
⇕
x[1]=argminF(x)forF(x)=12∆t2||x−x[0]−∆tv[0]||2M+E(x)
P15
Newton-Raphson Method
The Newton-Raphson method, commonly known as Newton’s method, solves the optimization problem: x[1]=argmin F(x). (F(x) is Lipschitz continuous.)
Given a current x(k), we approximate our goal by:
0=F′(x)≈F′(x(k))+F″
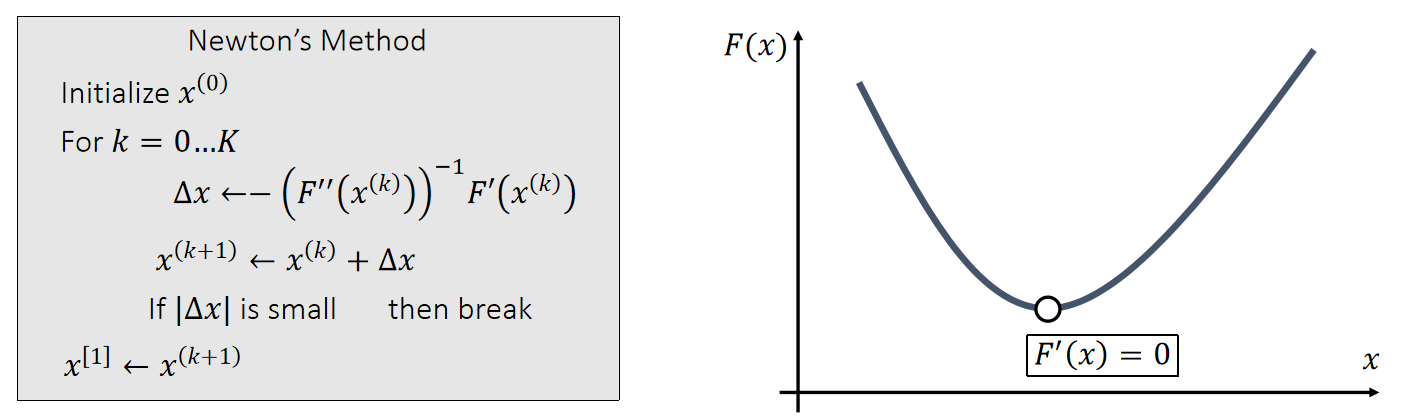
P16
Newton-Raphson Method
Now we can apply Newton’s method to: \mathbf{x} ^{[1]}= argmin F (\mathbf{x} ).
Given a current \mathbf{x}^{(k)}, we approximate our goal by:
\mathbf{0} =∇F(\mathbf{x} )≈∇F(\mathbf{x} ^{(k)})+\frac{∂F^2(\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} (\mathbf{x} −\mathbf{x} ^{(k)})
Newton’s Method
Initialize x^{(0)}
For k=0…K
∆\mathbf{x} \longleftarrow −(\frac{∂F^2(\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2})^{−1}∇F(\mathbf{x} ^{(k)}) \mathbf{x} ^{(k+1)}\longleftarrow \mathbf{x} ^{(k)}+∆\mathbf{x} If ||∆\mathbf{x}|| is small \quad\quadthen break
\mathbf{x} ^{[1]}\longleftarrow \mathbf{x} ^{(k+1)}
P17
Simulation by Newton’s Method
Specifically to simulation, we have:
F (\mathbf{x} )=\frac{1}{2∆t^2} ||\mathbf{x} −\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]}||_M^2+E(\mathbf{x} )
∇F(\mathbf{x} ^{(k)})=\frac{1}{∆t^2}\mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})−\mathbf{f} (\mathbf{x} ^{(k)})
\frac{∂^2F(\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} =\frac{1}{∆t^2}\mathbf{M} +\mathbf{H} (\mathbf{x} ^{(k)})
Initialize \mathbf{x}^{(0)}, often as \mathbf{x} ^{[0]} or \mathbf{x} ^{[0]} +∆t\mathbf{v} ^{[0]}
For k=0…K
\mathrm{Solve}\quad (\frac{1}{∆t^2} \mathbf{M+H} (\mathbf{x} ^{(k)}))∆\mathbf{x} =− \frac{1}{∆t^2}\mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})+\mathbf{f} (\mathbf{x} ^{(k)}) \mathbf{x} ^{(k+1)}\longleftarrow \mathbf{x} ^{(k)}+∆\mathbf{x} If ||∆\mathbf{x}|| is small \quad\quad then break
\mathbf{x} ^{[1]}\longleftarrow \mathbf{x} ^{(k+1)} \mathbf{v} ^{[1]}←(\mathbf{x} ^{[1]}−\mathbf{x} ^{[0]})/ ∆t
本文出自CaterpillarStudyGroup，转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/