A Height Field Model

高度场（Height Field）和速度场

高度场（Height Field）和速度场的定义

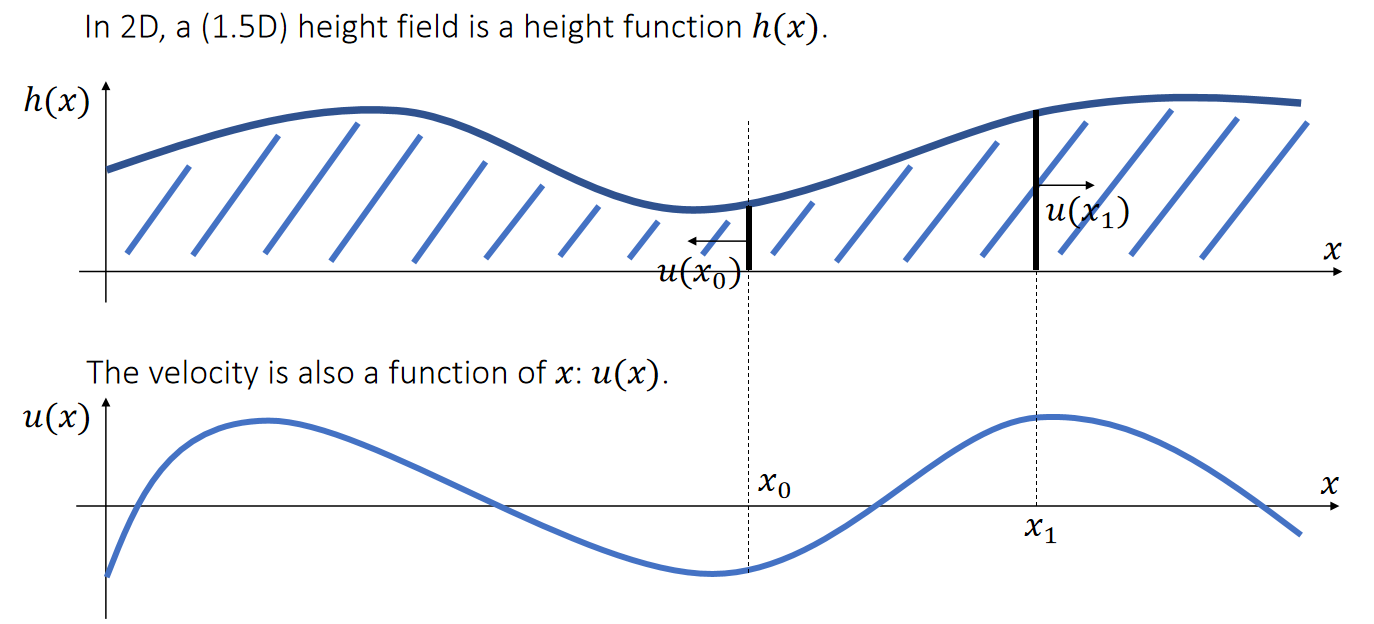
✅ 利用高度函数来表达波的平面，通过更新$h(x)$来表达水面随时间波动的效果。
✅ 由于用函数表达，无法描述大海浪的效果，因为这种情况下一个位置对应多个高度。
✅ 速度场描述水流的速度和方向，速度< 0 则右往左， > 0 则左往右。

高度场的更新

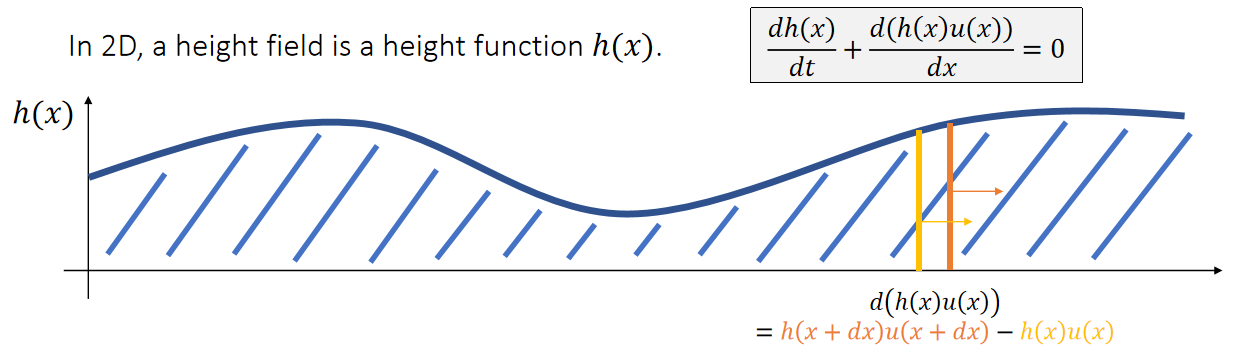
✅ 高度场更新公式第一项：高度场随时间的变化。
✅ 高度场更新公式第二项，根据微分的定义：
$h(x)u(x)$: 单位时间内流过x线的水量。
$d(h(x)u(x))$ ：单位时间内区域 $[x \quad x+dx]$ 的水量变化、
$d(h(x)u(x))1/dx$ ：单位时间内区域区 $[x \quad x+dx]$ 的水位高度变化

速度场的更新

The velocity is also a function of $x:u(x)$.

✅ 第一项：当水在流动时，速度应该跟水一起流动，下节课再讲。
✅ 第三项：外力，当前也不考虑。

Ignoring advection and external acceleration, we get a simple form:

$$ \begin{matrix} \frac{du(x)}{dt}=−\frac{1}{ρ} \frac{dP(x)}{dx} \quad \quad & ρ: \text{density} \quad \quad & P(x):\text{pressure} \end{matrix} $$

✅ 第二项：在短时间内、速度变化由左右压强差决定。同样的压强下，密度大则难推，密度小则好推。

Shallow Wave Equation

✅ 为什么叫 Shallow Wave, 因为该算法假设水波很小，因此 $dh / dx$ 可忽略不计。

We now have two equations:

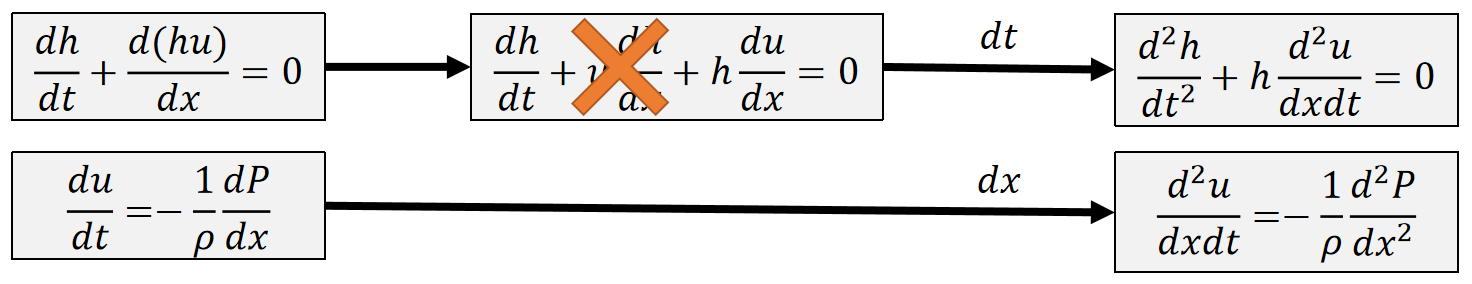
✅ 公式化简的目的：不需要关心速度场$u$、仅关注高度场就可以。
✅ 第一个公式：（1）对$d(hu)$展开（2）再求一次$dt$
✅ 第二个公式：对$x$求导

We can then eliminate $u$ and formulate the shallow wave equation:

$$\frac{d^2ℎ}{dt^2} =\frac{ℎ}{ρ} \frac{d^2P}{dx^2} $$

✅ 合并同类项，得到最终方程
✅ 但引擎无法直接处理微分程，因此要离散化开求解。

P10

高度场离散化

We discretize a continuous height field into a discrete set of height columns.

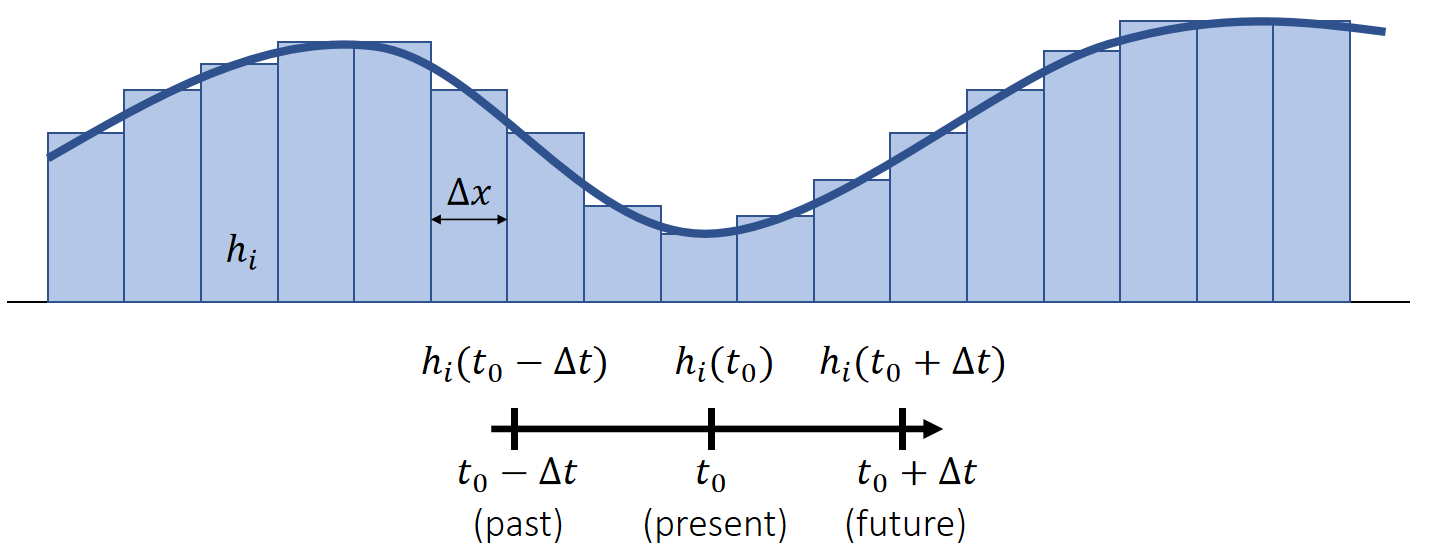
✅ 高度场离散又化为多个水柱，微分算子也要离散化。

P11

微分算子离散化

前向差分与后向差分

The idea of finite differencing is to use the difference to approximate the derivative.

$$ f(t_0+∆t)=f(t_0)+∆t\frac{df(t_0)}{dt} +\frac{∆t^2}{2} \frac{d^2f(t_0)}{dt^2} +… $$

Forward differencing (first-order)

$$\frac{df(t_0)}{dt} ≈\frac{f(t_0+∆t)−f(t_0)}{∆t}$$

$$ f(t_0−∆t)=f(t_0)−∆t\frac{df(t_0)}{dt}+\frac{∆t^2}{2}\frac{d^2f(t_0)}{dt^2} +… $$

Backward differencing (first-order)

$$ \frac{df(t_0)}{dt}≈\frac{f(t_0)−f(t_0−∆t)}{∆t} $$

P12

Central Differencing

The idea of finite differencing is to use the difference to approximate the derivative.

$$ f(t_0+∆t)=f(t_0)+∆t\frac{df(t_0)}{dt}+\frac{∆t^2}{2}\frac{d^2f(t_0)}{dt^2} +… $$

$$ f(t_0−∆t)=f(t_0)−∆t\frac{df(t_0)}{dt}+\frac{∆t^2}{2}\frac{d^2f(t_0)}{dt^2} +… $$

Central differencing (second-order)

$$ \frac{df(t_0)}{dt}≈\frac{f(t_0+∆t)−f(t_0−∆t)}{2∆t} $$

P13

二阶微分算子离散化

高度

We apply central differencing twice to estimate $d^2ℎ_i/dt^2$.

$$ \begin{matrix} \frac{dℎ_i(t_0+0.5∆t)}{dt}≈\frac{ℎ_i(t_0+∆t)−ℎ_i(t_0)}{∆t} \quad\quad& \frac{dℎ_i(t_0−0.5∆t)}{dt}≈\frac{ℎ_i(t_0)−ℎ_i(t_0−∆t)}{∆t} \end{matrix} $$

$$\frac{d^2ℎ_i(t_0)}{dt^2}≈\frac{\frac{dℎ_i(t_0+0.5∆t)}{dt}−\frac{dℎ_i(t_0−0.5∆t)}{dt} }{∆t} ≈\frac{ℎ_i(t_0+∆t)+ℎ_i(t_0−∆t)−2ℎ_i(t_0)}{∆t^2}$$

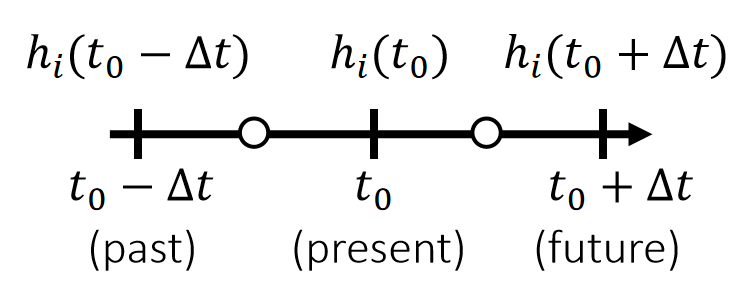
✅ 先用 central difference 求出两个中点的一阶导数，再基于此计算 $t_0$ 处的二阶导。这种操作又称为一维Laplace 算子。

P14

压强

Similarly, we apply central differencing twice to estimate $d^2P/dx^2$.

$$ \begin{matrix} \frac{dP_{i+0.5}}{dt} ≈\frac{P_{i+1}−P_i}{∆x} \quad\quad & \frac{dP_{i−0.5}}{dx} ≈\frac{P_i−P_{i−1}}{∆x} \end{matrix} $$

$$\frac{d^2P_i}{dx^2}≈\frac{\frac{dP_{i+0.5}}{dx}−\frac{dP_{i−0.5}}{dx}}{∆x} ≈\frac{P_{i+1}+P_{i−1}−2P_i}{∆x^2}$$

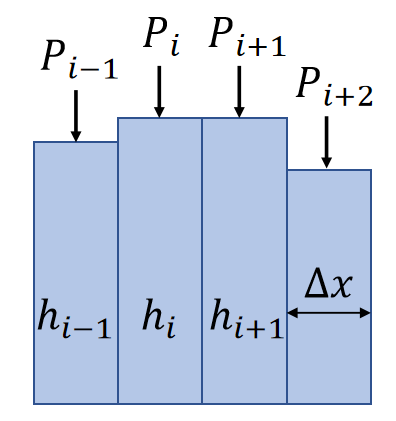
✅ 二维情况用周围4个元素，见 Games102 离散拉普拉斯算子。

P15

Discretized Shallow Wave Equation

We can now discretize the shallow wave equation $\frac{d^2ℎ}{dt^2}=\frac{ℎ}{ρ}\frac{d^2P}{dx^2}$.

$\begin{matrix}\ \frac{d^2ℎ_i(t_0)}{dt^2}≈\frac{ℎ_i(t_0+∆t)+ℎ_i(t_0−∆t)−2ℎ_i(t_0)}{∆t^2}\quad &\frac{d^2P_i}{dx^2 }≈\frac{P_{i+1}+P_{i−1}−2P_i}{∆x^2}\\\end{matrix}$

$\quad$

$\Rightarrow \frac{ℎ_i(t_0+∆t)+ℎ_i(t_0−∆t)−2ℎ_i(t_0)}{∆t^2}=\frac{ℎ_i}{ρ} (\frac{P_{i+1}+P_{i−1}−2P_i}{∆x^2})$

$\quad$

$\Rightarrow ℎ_i(t_0+∆t)=2ℎ_i(t_0)−ℎ_i(t_0−∆t)+\frac{∆t^2ℎ_i}{∆x^2ρ}(P_{i+1}+P_{i−1}−2P_i)$

✅ 更新目标：下一个时刻的水柱的高度，即 $h_i(t_0 + ∆t)$
✅ 但按此公式模拟可能出现水的体积变多或变少的问题。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/