P11

粒子碰撞检测 --- SDF

Signed Distance Function

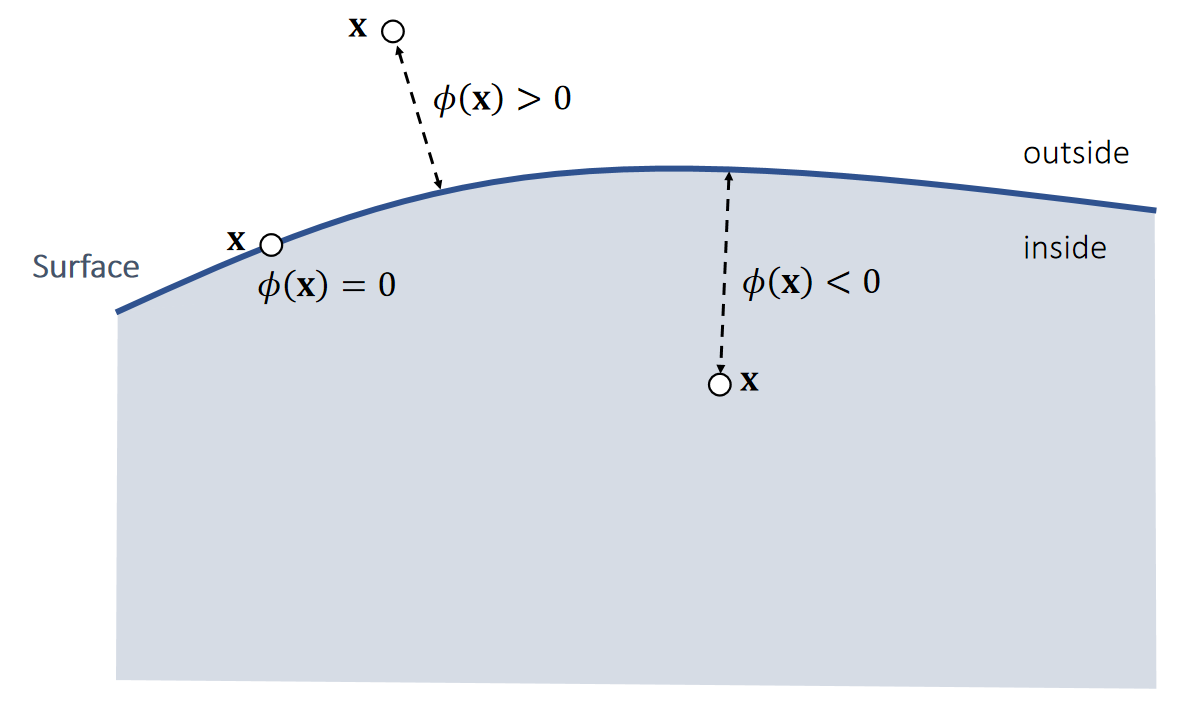
A signed distance function $\phi (\mathbf{x} )$ defines the distance from $\mathbf{x}$ to a surface with a sign. The sign indicates on which side $\mathbf{x}$ is located.

P12

Signed Distance Function Examples

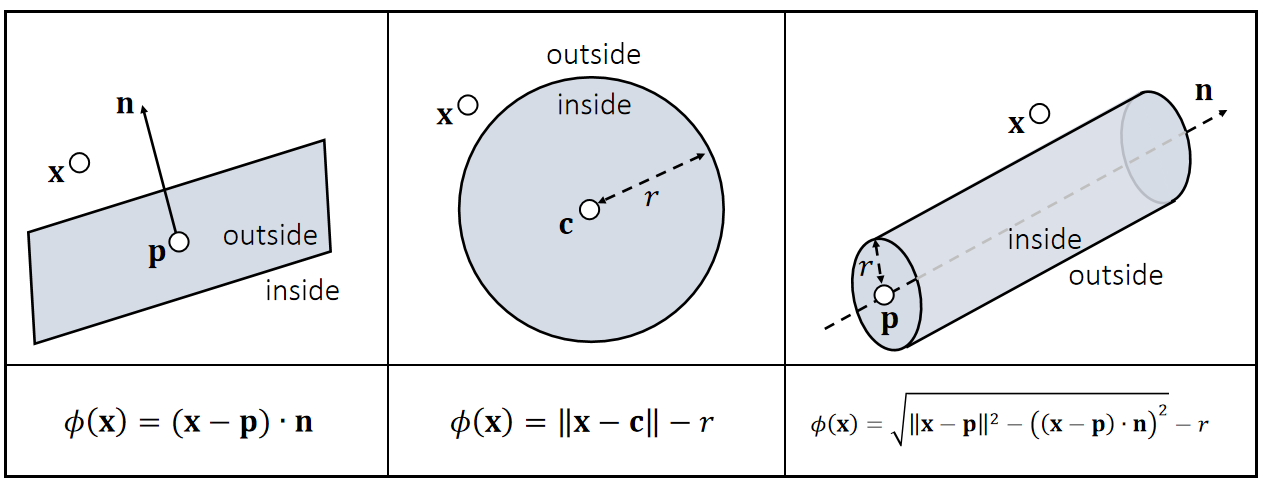
✅ 圆柱SDF基于勾股定理，$\sqrt{\cdot }$ 内第一项为斜边长，第二项为底边长，得出点到中轴的距离。

P13

Intersection of Signed Distance Functions

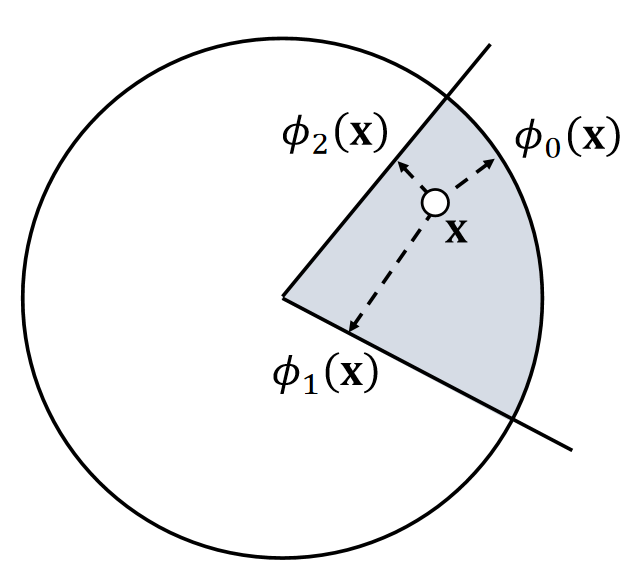
If $\phi _0(\mathbf{x} )<0$ and $\phi_1(\mathbf{x} )<0$ and $\phi_2(\mathbf{x} )<0$
then inside
$\quad \phi (\mathbf{x} )$=max $⁡(\phi_0(\mathbf{x}),\phi_1(\mathbf{x}),\phi_2(\mathbf{x}))$
Else outside
$\quad \phi (\mathbf{x})=?$

P14

Union of Signed Distance Functions

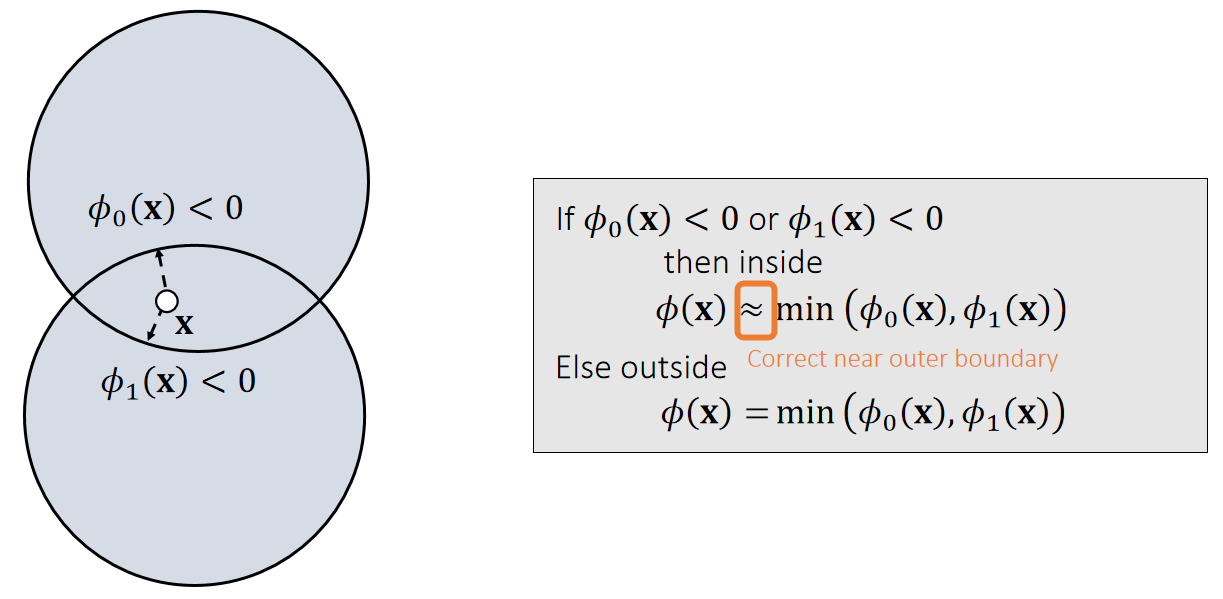
✅ 有时候此公式不成立，例如图中$\mathbf{x}$ 点

Intuitively, we can consider collision detection with the union of two objects as collision detection with two separate objects.

P15

穿透检测

$$ \phi (x(t))=0 $$
解出 $t$
如果 $t$ 在所检测的时间范围内有解，则说明存在穿透 $t$ 为穿透时刻。

粒子碰撞响应 —— Penalty Method

碰撞解除

SDF 常用于代表静态物体，这种物体不响应力和碰撞，所以所有的碰撞响应都发生在粒子上。

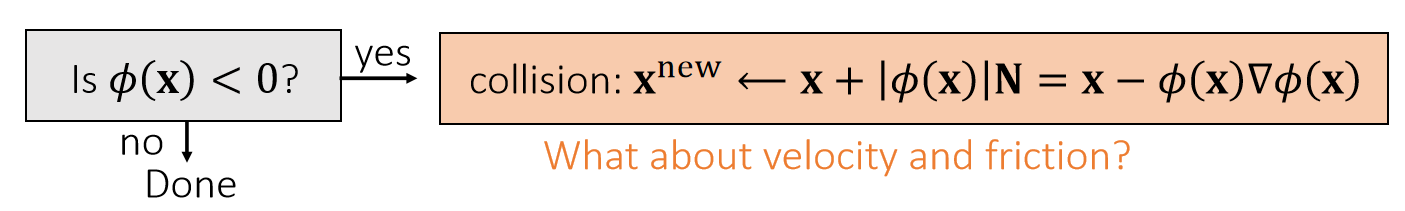
✅ 更新方向：N方向。更新距离：穿入的距离。

状态更新

Quadratic Penalty Method

A penalty method applies a penalty force in the next update. When the penalty potential is quadratic, the force is linear.

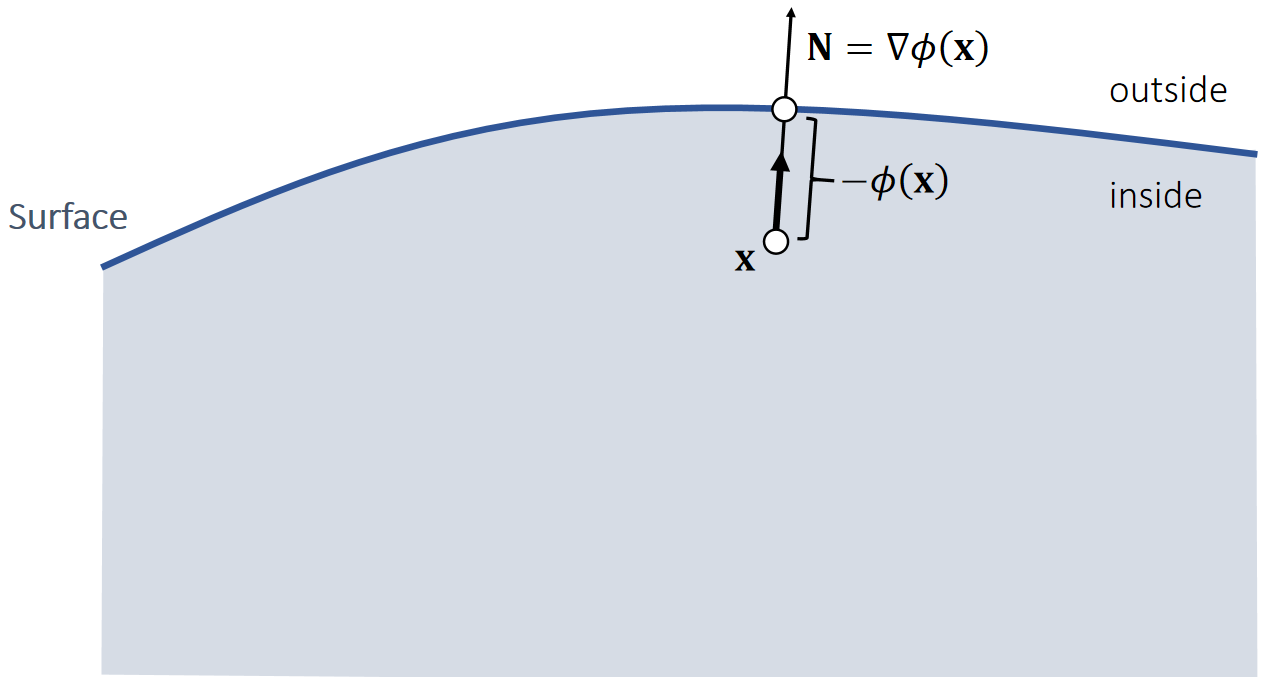
当粒子进入物体内部后，就会产生一个向外的推力。

✅ 力的大小与距离有关，方向为normal
✅ 存在的问题：只有$\mathbf{x}$ 进入 mesh 内部了，才会有力，但此时穿透的 artifacts 已经产生了。解决方法：使用buffer

P16

粒子的运动状态发生变化确实是由于力的作用。但对力的大小的假设均不合理。
力的大小确实与穿透深度有关，因为：

穿透深 → 相对速度大 → 碰撞速度和反弹速度都大 → 速度改变大 → 力大

Quadratic Penalty Method with a Buffer

A buffer helps lessen the penetration issue. But it cannot strictly prevent penetration, no matter how large $k$ is.

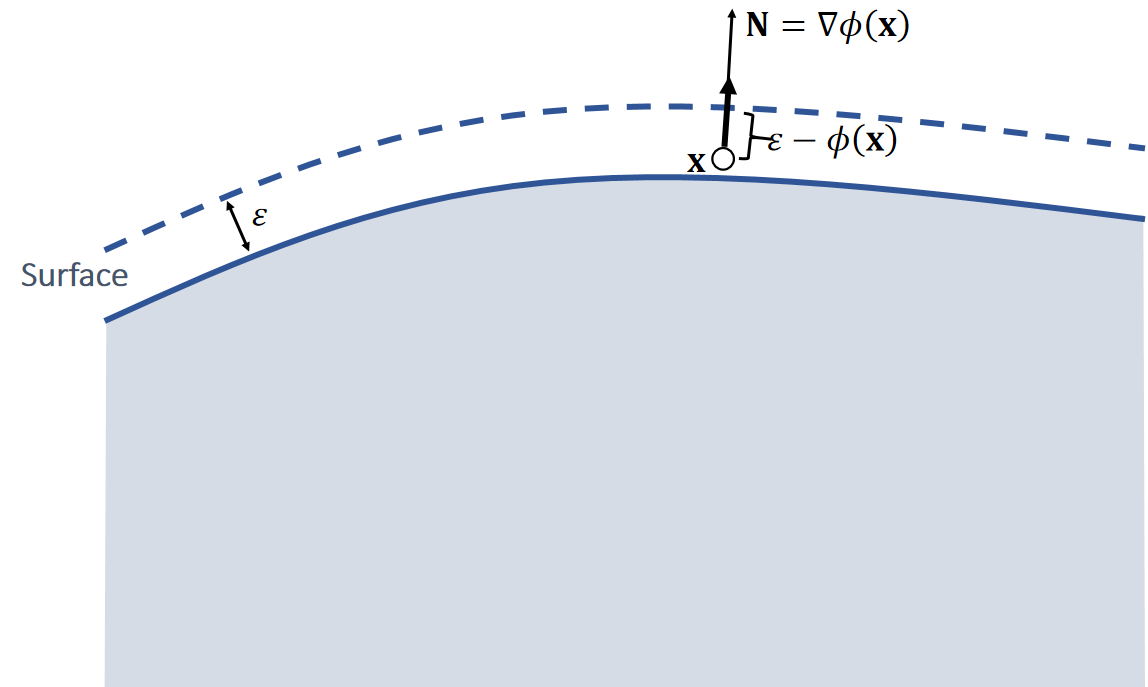
✅ 存在的问题：
如果 $k$ 太小，快速的碰撞仍会产生 artifacts
如果 $k$ 太大，碰撞的反弹过于强烈(overshooting)
解决方法：不用常数 $k$ ，而是 $k$ 与距离相关

P17

Log-Barrier Penalty Method

A log-barrier penalty potential ensures that the force can be large enough. But it assumes $\phi (\mathbf{x} ) < 0$ will never happen!!! To achieve that, it needs to adjust $\Delta t$.

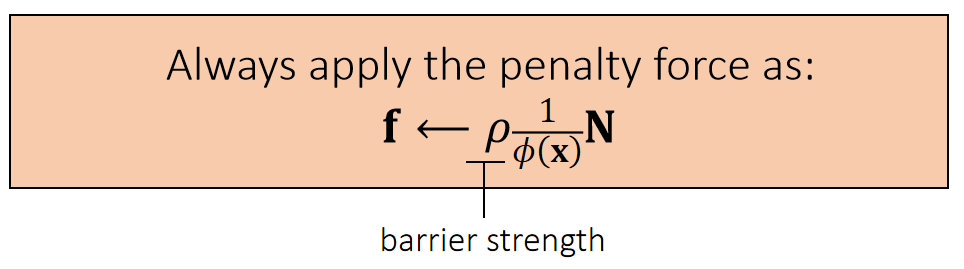
✅ 用倒数关系代替线性关系。
✅ 存在的问题：
1.当$\mathbf{x}$ 靠近物体表面时，仍然会 overshooting
2.$\mathbf{x}$ 穿透表面后，会越陷越深。
3.本算法如果要求保证穿透永远不会发生，因此要仔细调节 $\Delta t$.

P18

A Short Summary of Penalty Methods

The use of step size adjustment is a must.
- To avoid overshooting.
- To avoid penetration in log-barrier methods.
Log-barrier method can be limited within a buffer as well.
- Li et al. 2020. Incremental Potential Contact: Intersection- and Inversion-free Large Deformation Dynamics. TOG.
- Wu et al. 2020. A Safe and Fast Repulsion Method for GPU-based Cloth Self Collisions. TOG.
Frictional contacts are difficult to handle.

✅ 缺点：
(1) 难以模拟摩擦。
(2) 碰撞 → 施加力 → 调整，因此效果是滞后的。
优点：易实现

P19

Particle Collision Response —— Impulse Method

An impulse method assumes that collision changes the position and the velocity all of sudden.

✅ Penalty 方法是碰撞 → 力 → 下一时刻的速度和位置，效果滞后。
✅ Impulse方法碰撞时立即更新速度和位置

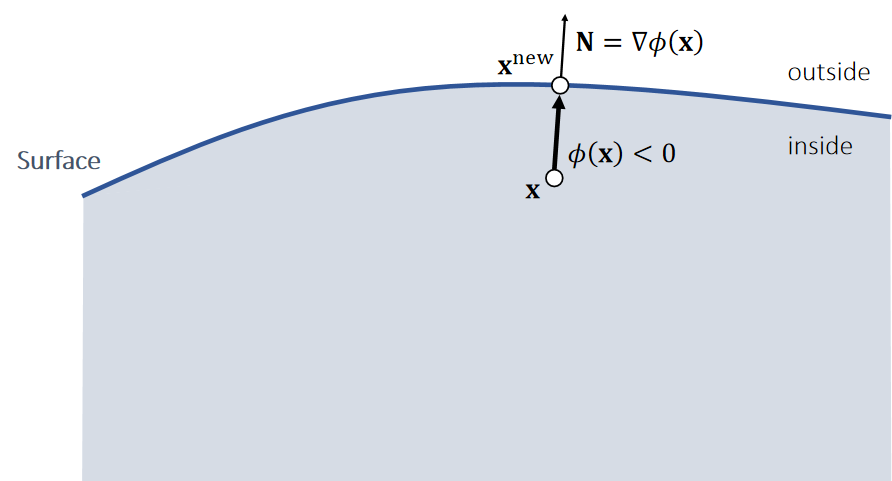
✅ lmpulse 省去了力这一步，直接更新刚体状态。方法要求已经有一个比较好的$\phi (x)$
✅ 关键区别不在于是否使用力，而是位置是怎样计算出来的，前者的位置由力和速度，这个计算出来的(不管是作为下一时刻还是这一时刻)的位置，都不能保证一定能以物体内部推出来，但后者直接求出当前置对应的表面位置的点，并更新上去，因此能立即生效。

更新速度

P20
Changing the position is not enough, we must change the velocity as well.

✅ $\mathbf{v}\cdot \mathbf{N}\ge 0$：当前速度想要让物体越陷越深, 这种情况下才需要更新速度

✅ 把$\mathbf{v}$分解为$\mathbf{v_T}$（切线方向的速度）和$\mathbf{v_N}$（法线方向的速度）.
✅ $\mathbf{v_N}$方向速度反弹， $\mu _\mathbf{N}$ 为反弹系数。$\mathbf{v_N}$方向不变或由于摩擦而衰减
✅ a的约束：（1）越小越好，尽量把速度衰减掉（2）满足库仑定律（切方向的速度改变不应大于法线方向的速度改变）（3）切方向速度不能反转，即a不能为负

Impulse方法总结

✅ 优点：可以精确控制摩擦力和反弹位置。缺点：计算比 Penalty 复杂
✅ 刚体常见于 Impulse；弹性体常见于Penalty.

	速度大小	速度方向
Penalty	碰撞深度->力的大小	表面方向
Impulse	相对速度 * decay	反弹方向+惯性方向

粒子与 Mesh

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/