P4
弹簧结构
An Ideal Spring
An ideal spring satisfies Hooke’s law: the spring force tries to restore the rest length.
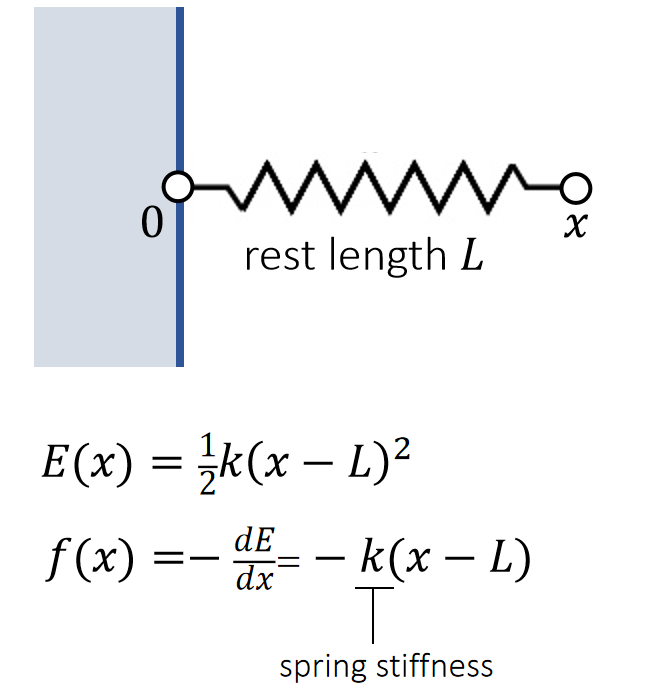
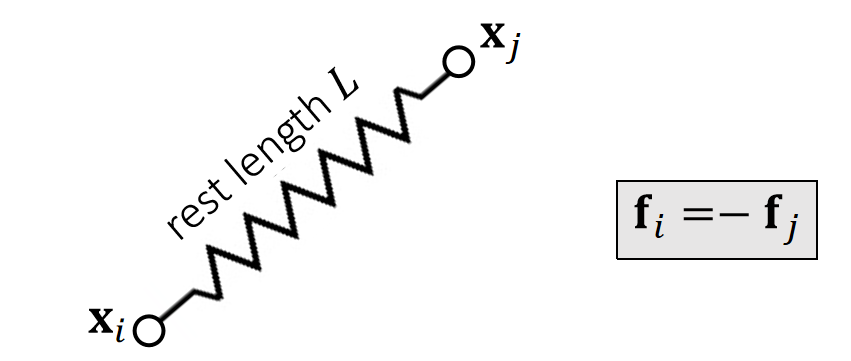
\(E(\mathbf{x})=\frac{1}{2}k (||\mathbf{x}_i −\mathbf{x}_j||−\mathbf{L} )^2\)
\(\mathbf{f} _i(\mathbf{x} )=−∇_i\mathbf{E} =−k(||\mathbf{x}_i −\mathbf{x}_j||−L)\frac{\mathbf{x}_i −\mathbf{x}_j}{||\mathbf{x}_i −\mathbf{x}_j ||}\)
\(\mathbf{f} _j(\mathbf{x})=−∇_jE=−k (||\mathbf{x}_j −\mathbf{x}_i ||−L)\frac {\mathbf{x}_j −\mathbf{x}_i}{||\mathbf{x}_j −\mathbf{x}_i||}\)
P5
Multiple Springs
When there are many springs, the energies and the forces can be simply summed up.
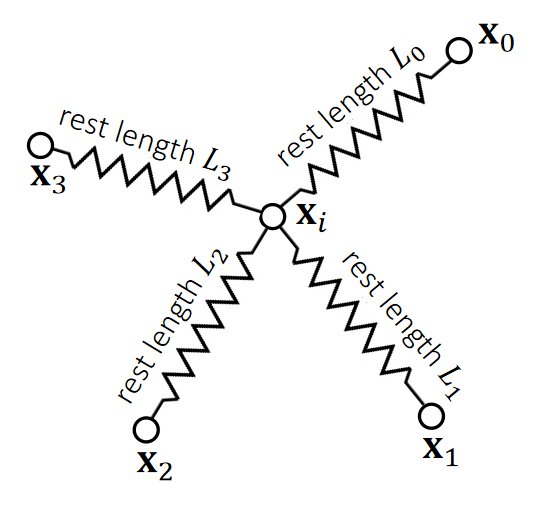
$$ E= {\textstyle \sum_{e=0}^{3}}E_e= {\textstyle \sum_{e=0}^{3}} (\frac{1}{2} k(||\mathbf{x} _i −\mathbf{x}_e ||−L_e)^2) $$
$$ f_i=−\nabla_iE = \textstyle \sum_{e=0}^{3}(−k(||\mathbf{x}_i−\mathbf{x}_e||−L_e)\frac{\mathbf{x}_i−\mathbf{x}_e}{||\mathbf{x}_i−\mathbf{x}_e||}) $$
✅ 能量和力都是可以叠加的
P6
Structured Spring Networks
✅ 绿线：防止斜方向的拉伸。蓝线：防止翻折。
P7
Unstructured Spring Networks
We can also turn an unstructured triangle mesh into a spring network for simulation.
✅ 蓝线：抵抗弯曲。对每条内部边，加这样一根弹簧。
P8
怎样基于三角形Mesh增加蓝线弹簧
The basic representation of a triangle mesh uses vertex and triangle lists.
✅ 已知边的信息，需找出内部边，例如\(\mathbf{x}_0\mathbf{x}_3\)，因此要基于此构造边：\(\mathbf{x}_1x 4\)
✅ Each triangle has three edges. But there are repeated ones. Repeated edges就是内部边。
✅ 1. 找出内部边。2. 找出内部边所属于的两个三角形。3. 找出两个三角形上不在这条内部边上的点。4. 连续一根弹簧。
Vertex list: {\(\mathbf{x} _0, \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4\)} (3D vectors)
Triangle list: {1, 2, 3, 0, 1, 3, 0, 3, 4} (index triples)
The key to topological construction is to sort triangle edge triples.
Each triple contains: edge vertex index 0, edge vertex index 1 and triangle index (index 0<index).
✅ 排序：基于边排序，排序后相同边会靠在一起
P11
积分系统
Explicit Integration of A Mass-Spring System
✅ 整体流程跟刚体运动很像，只是力变得复杂，每个弹簧端点上受到的力都要考虑，但没有了旋转。
✅ \( E [e] [0] ：e\)代表弹簧 ID:0或1代表弹簧两个端点
❗ 图画得不对，先提前把所有的力都算出来，再遍历所有顶点
P12
Explicit integration suffers from numerical instability caused by overshooting, when the stiffness \(k\) and/or the time step \(∆t\) is too large.
✅ Explicit：当前力 → 当前速度 → 当前位置
根据公式\(FΔt≈mv，vΔt≈Δx\)，如果\(Δt\)太大，会导致\(Δx\)太大，而导致overshooting。
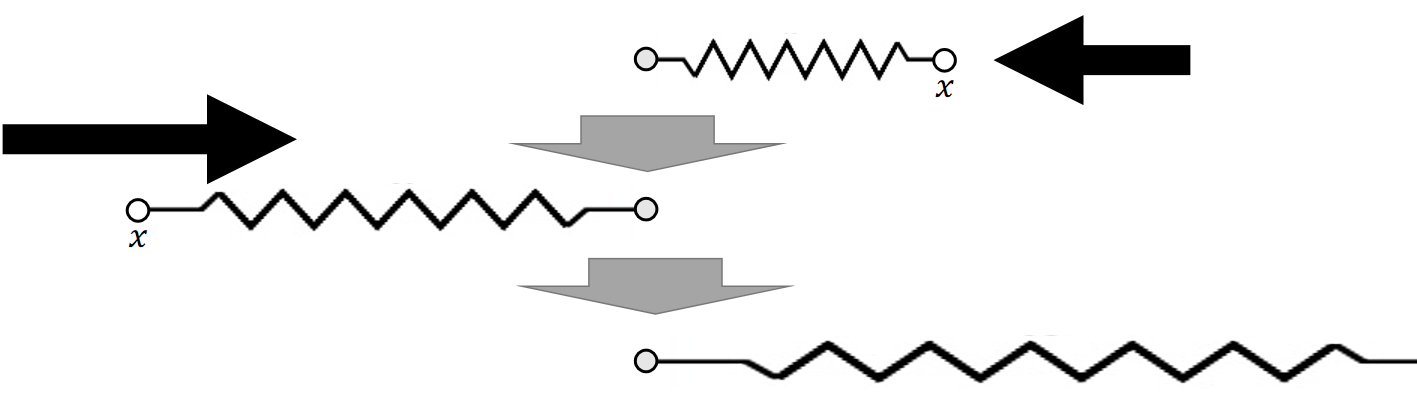
A naive solution is to use a small \(∆t\) . But that slows down the simulation.
✅ 解决方法：减小\(\Delta t\)。但这个方法不解决本质问题，且会降低整个模拟系统的效率
✅ 本质上是\(Δt\)太大导致积分近似的结果与实际积分的结果有很大误差，\(k\)太大或\(Δt\)只是让这个问题更明显，减小\(k\)或\(Δt\)问题仍然存在。
P13
Implicit Integration
Implicit integration is a better solution to numerical instability. The idea is to integrate both x and v implicitly.
✅Explicit和Implicit都是用某个时刻的力代表整个\(Δt\)时间的力，就都会出现上述误差。
区别在于，Explicit用当前力，往往使结果变大，产生爆炸，Implicit用未来力，往往使结果变小，产生消失。
✅ 消失只是结果不对。但爆炸会让结果崩溃，这对是最不可接受的问题。因此用隐式代替显式。
消元得：
✅ 下面公式1通过把上面公式1代入公式2得到。下面公式2通过把上面公式写反推得到。
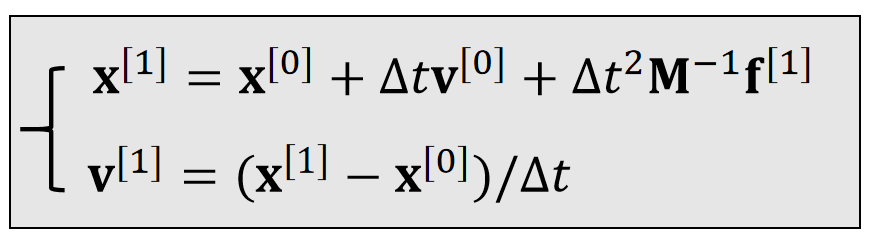
Assuming that \(\mathbf{f}\) is holonomic, i.e., depending on \(\mathbf{x}\) only, our question is how to solve:
$$
\mathbf{x} ^{[1]}=\mathbf{x}^{[0]}+∆t\mathbf{v} ^{[0]}+∆t^2\mathbf{M} ^{−1}\mathbf{f} (\mathbf{x}^{[1]})
$$
✅ holonomic：力的大小和方向只跟位置有关，跟速度无关。例如重力，弹力。那么 \(f\)可以写成关于位置的函数\(f(x)\)。
✅ 但\(f(x)\)不一定是线性的。因此最后转化为解非线性方程的问题。未知量为\({x} ^{[1]}\)
P14
\(\mathbf{x} ^{[1]} =\) argmin \(F(\mathbf{x})\quad\) for \(\quad F(\mathbf{x}) = \frac{1}{2∆t^2}||\mathbf{x} −\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]}||_M^2+E(\mathbf{x} )\)
✅ 前面方程解\({x} ^{[1]}\)等价于F(x)函数极小点。等价转换的推导在补充1。非线性方程问题为转化为优化问题。
其中：\(\mathbf{M}\)对角矩阵，描述质量，\(3N \times 3N\)。\(\mathbf{x}\)为 \(3N\times 1\)矢量,描述顶点信息。\(E\) 为所有的力的能量。\(\mathbf{||x||_M^2=x^TMx} \)。
✅ 只有保守力能用能量描述、非保守力（例如摩擦力）则不行。
P15
优化方法
P18
Simulation by Newton’s Method
🔎 Newton-Raphson Method见补充2. 这里直接开始Newton方向本当前场景的应用。
Specifically to simulation, we have:
$$ F (\mathbf{x} )=\frac{1}{2∆t^2}||\mathbf{x} −\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]}||_\mathbf{M} ^2+\mathbf{E} (\mathbf{x} ) $$
$$ ∇F(\mathbf{x}^{(k)})=\frac{1}{∆t^2}\mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})−\mathbf{f}(\mathbf{x}^{(k)}) $$
$$ \frac{∂^2F (\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} =\frac{1}{∆t^2} \mathbf{M} +\mathbf{H} (x^{(k)}) $$
❓ 每一个 step 都包含一次迭代优化、能做到实时？
✅ 本节课所讲的套路：分析力 → 隐式积分 → 优化问题 → 更新，对弹簧系统、有限元、弹性体等各种物理模拟同样适用
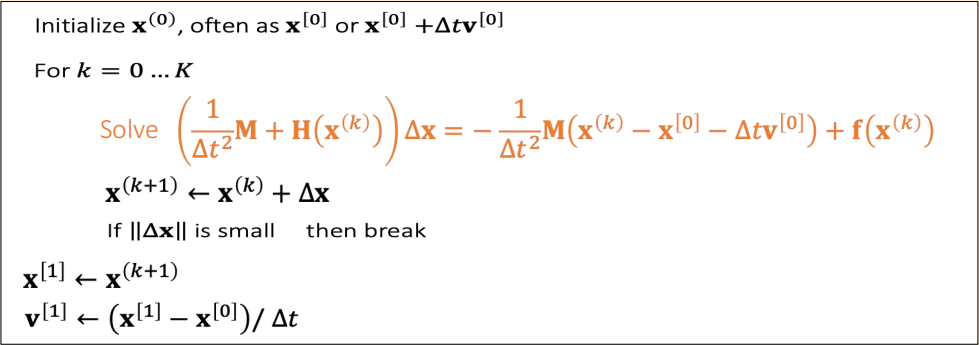
✅ 早期的方式不是用优化来做的，而是近似成线性问题后直接解方程组。这种方法相当于每一个Step做了一次牛顿法。
P19
Solve Spring Hessian
According to Lecture 2, Page 48,
✅ 弹簧系统的H是由所有弹簧的H构成的。
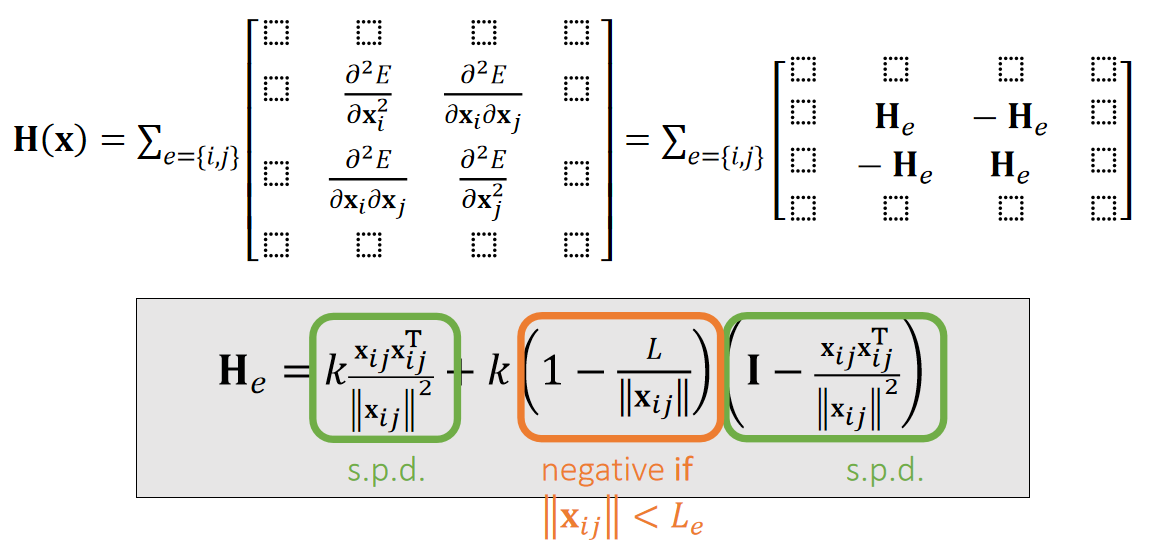
✅ \(H(x)\)的维度是\(3N \times 3N\)，N 是弹簧数。每个\(H_e\)的维度是\(3 \times 3\)。
✅ 课后答疑：质点的质量可以不同吗？
答：可以不同。先根据三角形的面积计算三角的质量，再把质量分配到各个顶点上。
Positive Definiteness of Hessian
✅ \(H(x)\)的正定性由\(H_e\)的正定性决定。
下面分析\(H_e\)的正定性：
For any \(\mathbf{x} _{ij}, \mathbf{v} ≠0\),
$$ \mathbf{V}^\mathbf{T}\frac{{\mathbf{x} _{ij}\mathbf{x} _{ij}}^\mathbf{T} }{||\mathbf{x} _{ij}||^2}\mathbf{V}=||\frac{{\mathbf{x} _{ij}}^\mathbf{T} \mathbf{v} }{||\mathbf{x} _{ij}||}||^2> 0 $$
$$ \mathbf{V} ^\mathbf{T} (\mathbf{I} -\frac{{\mathbf{x} _{ij}\mathbf{x} _{ij}}^\mathbf{T} }{||\mathbf{x} _{ij}||^2}) \mathbf{V} =\frac{||\mathbf{x} _{ij}||^2||\mathbf{v} ||^2-||{\mathbf{x} _{ij}}^\mathbf{T} \mathbf{v} ||^2}{||\mathbf{x} _{ij}||^2}\ge 0 $$
✅ \( \mathbf{x}_ {ij}\) 代表顶点\( \mathbf{x}_ {i}\)和顶点\( \mathbf{x}_ {j}\)的位置的差。
✅ 最后一个公式分子满足柯西不等式
✅ 结论：\(||x_{ij}||< Le\). 代表弹簧处于压缩状态。此时 He 有可能非正定，但拉伸时一定正定。
He 正定则\(H(x)\)半正定，此时弹簧系统有唯一解。
P20
When a spring is stretched, \(\mathbf{H} _e\) is s.p.d.; but when it’s compressed, \(\mathbf{H} _e\) may not be s.p.d.
As a result, \(\mathbf{H}(\mathbf{x})\) may not be s.p.d. (Lecture 2, Page 36).
\(\mathbf{A}\) may not be s.p.d. either.
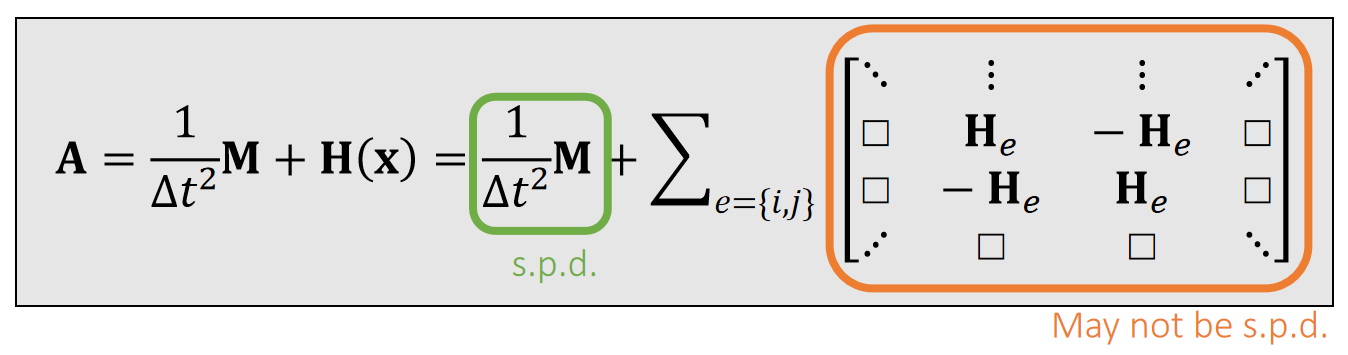
✅ \(\Delta t\)越小，A越容易正定、弹簧系统越稳定。
✅为什么要讨论\(H\)矩阵是否正定？答：\(H\)矩阵相当于二阶导，正定代表开口向上，有唯一最小值。
✅ 但是A不正定，不代表没有唯一解。
P22
When a spring is compressed, the spring Hessian may not be positive definite. This means there can be multiple local minima (outcomes).
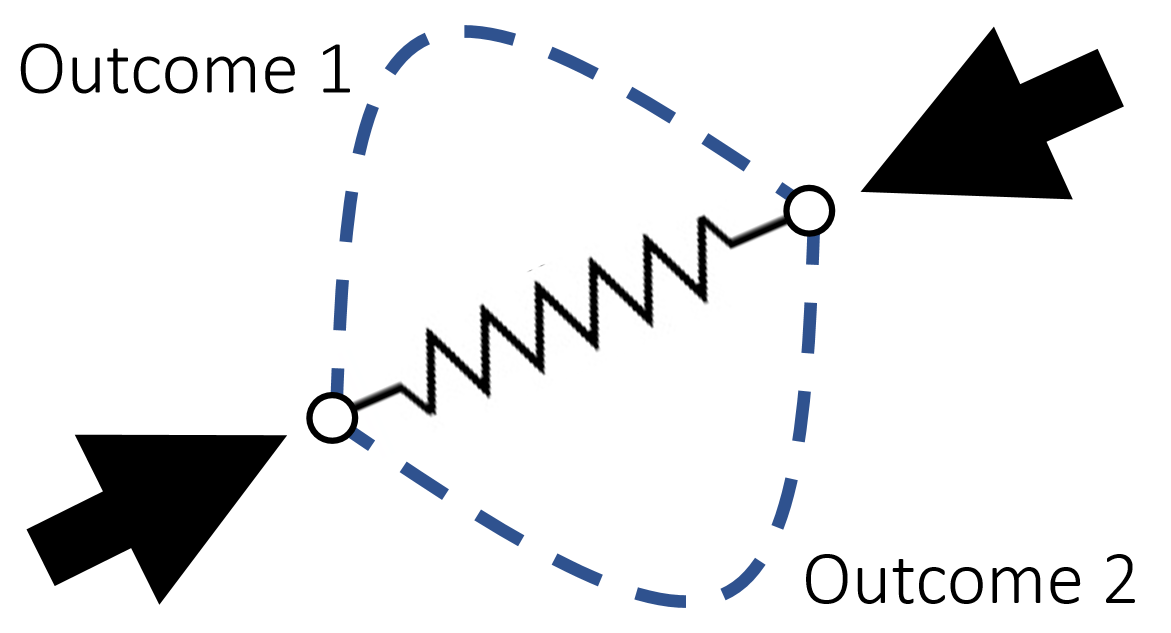
| Note: This issue occurs only in 2D and 3D. In 1D, \(E(x)=\frac{1}{2} k(x−L)^2\) and \({E}''(x)=k>0\). |
|---|
P23
Enforcement of Positive Definiteness
- Nevertheless, some linear solvers can fail to work if the matrix \(\mathbf{A}\) in \(\mathbf{A}\Delta \mathbf{x}=\mathbf{b}\) is not positive definite.
✅ 不正定最大的问题不是解不唯一，因为解出任意一个解都能让模拟系统进行下去。
非正定的主要问题，是数学计算上的不稳定，可能导致解不出来；
- One solution is to simply drop the ending term, when \({\color{Orange}{ ||\mathbf{x} _{ij}||<\mathbf{L} _e}}:\)
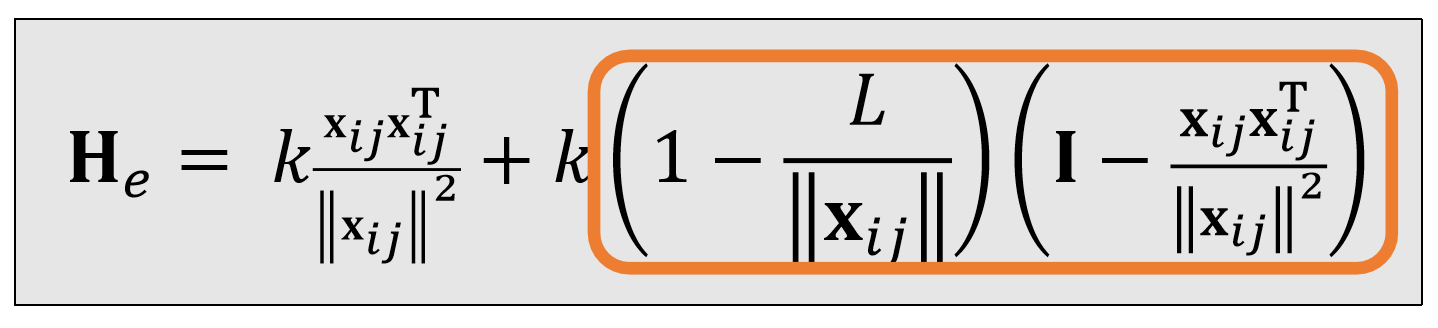
✅ 简单粗爆的解决方法就是把后面这项删掉。
- Other solutions exist. For example,
🔎 Choi and Ko. 2002. Stable But Responive Cloth. TOG (SIGGRAPH)
P24
Linear Solvers
The Jacobi Method
We can use the Jacobi method to solve \(\mathbf{A}∆\mathbf{x} = \mathbf{b} \).
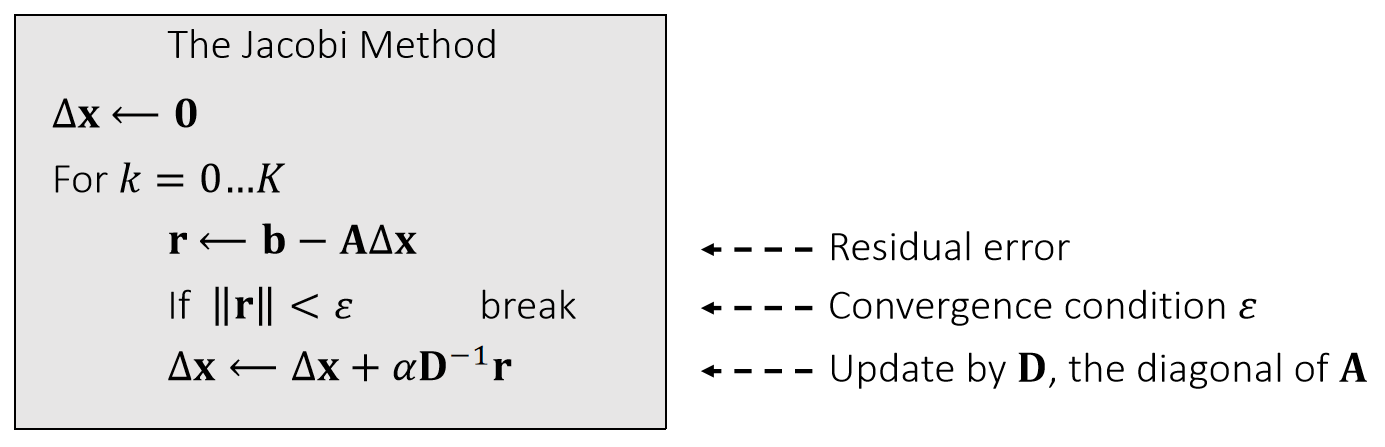
The vanilla Jacobi method (\(α\) = 1) has a tight convergence requirement on \(\mathbf{A}\), i.e., being diagonal dominant.
The use of \(α\) allows the method to converget even when \(\mathbf{A}\) is positive definite only.
P25
An Incomplete Summary
- Direct Solvers (LU, LDLT, Cholesky, …)
- One shot, expensive but worthy if you need exact solutions.
- Little restriction on \(\mathbf{A}\)
- Mostly suitable on CPUs
🔎 Intel MKL PARDISO
- Iterative Solvers
- Expensive to solve exactly, but controllable
- Convergence restriction on \(\mathbf{A}\), typically positive definiteness
- Suitable on both CPUs and GPUs
- Easy to implement
- Accelerable: Chebyshev, Nesterov, Conjugate Gradient…
✅ 课后答疑
问题二：怎么加速？
答：用 Jacobian 可以在 GPU 上加速、直接法比迭代法慢。
问题三：共轭梯度
共轭梯度的效率很大程度上取决于 precondition,但在GPU上能使用的precondition 比较受限、 CPU 上一般选择 Incomplete LU 分解。
问题四：支持的维度
直接法比较占内存，因此支持的维度不如迭代法大。
P26
The Jacobi Method with Chebyshev Acceleration
We can use the accelerated Jacobi method to solve \(\mathbf{A}∆\mathbf{x} =\mathbf{b} \).
The Accelerated Jacobi Method
\(∆\mathbf{x} \longleftarrow \mathbf{0} \)
last_\(∆\mathbf{x} \longleftarrow \mathbf{0}\)
For \(k=0\dots \mathbf{K}\)
\(\mathbf{r} \longleftarrow \mathbf{b} −\mathbf{A} ∆\mathbf{x}\)
If \(||\mathbf{r} ||<\omega \quad\) break
If \(k=0 \quad\quad\quad \omega =1\)
Else If \( k=1 \quad \quad\quad\omega =2/(2-\rho^2)\)
Else \(\quad\quad\quad\omega =4/(4-\rho ^2\omega )\)
old_\(∆ \mathbf{x} \longleftarrow ∆ \mathbf{x}\)
\(∆\mathbf{x} ⟵∆\mathbf{x} +\mathbf{αD} ^{−1}\mathbf{r}\)
\(∆\mathbf{x} \longleftarrow \omega ∆ \mathbf{x} +(1−\omega)\)last_∆\(\mathbf{x}
\)
last_\(∆\mathbf{x} \longleftarrow \) old_\(∆\mathbf{x}\)
| \(\rho (\rho <1)\) is the estimated spectral radius of the iterative matrix. |
|---|
✅ 这一页老师没讲
P27
After-Class Reading
Baraff and Witkin. 1998. Large Step in Cloth Simulation. SIGGRAPH.
One of the first papers using implicit integration.
The paper proposes to use only one Newton iteration, i.e., solving only one linear system. This practice is fast, but can fail to converge.
✅这篇论文是衣服模拟的经典论文，第一个用隐式积分做衣服模型的论文。
论文没有用弹簧系统，而是另一套模型。
没有做非线性优化或解非线性方程，而是把非线性方程线性化，等价于做一次牛顿迭代。
补充1：非线性方程求解
求解的非线性方程如下，其中\({x} ^{[1]}\)是未知量。
$$
\mathbf{x} ^{[1]}=\mathbf{x}^{[0]}+∆t\mathbf{v} ^{[0]}+∆t^2\mathbf{M} ^{−1}\mathbf{f} (\mathbf{x}^{[1]})
$$
P14
$$ \mathbf{||x||_M^2=x^TMx} $$
✅ Note that this is applicable to every system, not just a mass-spring system.
把公式处理一下得，
$$
x^{[0]}+Δtv^{[0]}+Δt^2M^{-1}f(x^{[1]})-x^{[1]}=0
$$
左右两边同时乘以\(\frac{M}{Δt^2}\)得
$$
\frac{1}{Δt^2} M(x^{[1]}-x^{[0]}-Δtv^{[0]})-f(x^{[1]})=0
$$
这里面唯一的未知量是\(x^{[1]}\)，定义函数
$$
y=\frac{1}{Δt^2} M(x-x^{[0]}-Δtv^{[0]})-f(x)
$$
当\(x = x^{[1]}\) 时，\(y = 0\), 即 \(y(x^{[1]}) = 0\)
从另一个角度讲，
$$
\begin{eqnarray}
x^{[1]} & = \mathrm{argmin}& F(x)\Rightarrow {F}' (x^{[1]}) & = & 0
\end{eqnarray}
$$
因此, \({F}' (x) = y. \quad F(x) = \int ydx \)
补充2：Newton-Raphson Method
x是值的F(x)函数
The Newton-Raphson method, commonly known as Newton’s method, solves the optimization problem: \(x^{[1]}\) = argmin \(F(x)\).
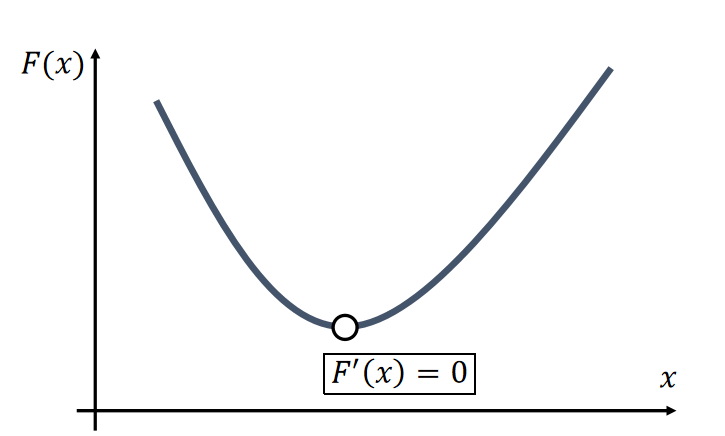
Given a current \(x^{(k)}\), we approximate our goal by:
$$ 0={F}' (x)≈{F}'(x^{(k)})+{F}'' (x^{(k)})(x−x^{(k)}) $$
✅ \(a = \min F(x)⇒ F'(a)= 0\)，\({F}' (x)\) 是非线性函数，直接解\({F}' (x)=0\) 很难解
✅ 对\({F}'(x)\) 做一阶泰勒展开，保留到二阶项。
假设\(x^{[k]}\)为任意已知值，就变成了解线性方程，很容易解出\(x\).
因为\({F}'(x)\) 是一个近似的，\(x\) 也是一个近似解。但\(x^{[k]}\) 越接近真实解，\(x\) 也会越接近真实解。因此，选代是\(x^{[k]}\)和\(x\) 都不断逼近真实解的过程。
✅ 普通的梯度下降是把\({F}' (x)\) 近似到一阶，牛顿法是近似到二阶，因此下降更快。
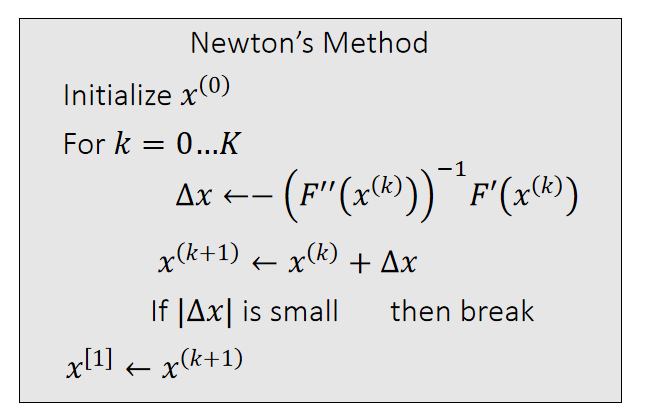
✅ Overshooting 的本质：误差会积累和放大
P16
Newton’s method finds an extremum, but it can be a minimum or maximum.
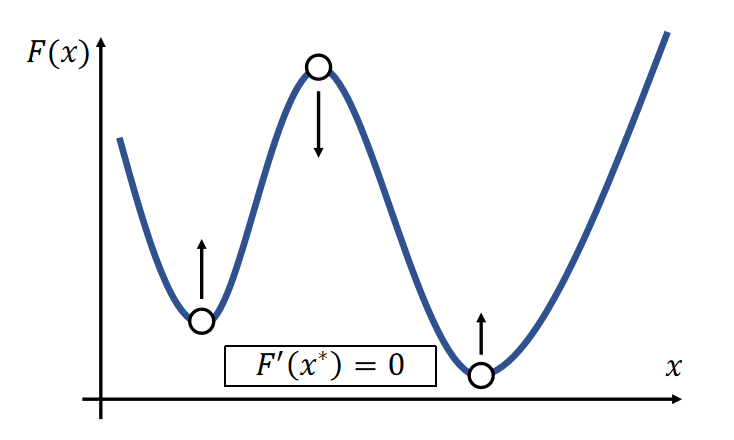
- At a minimum \(x^∗, {F}'' (x^∗)>0\).
- At a maximum \(x^∗, {F}''(x^∗)<0\).
- If \({F}''(x)>0\) is everywhere, \(F(x)\) has no maximum. \(=> F(x)\) has only one minimum.
✅ \(F'(a)= 0,a\) 有可能是最大值或最小值，因此要判定解是否合理。判定方法： \({F}''(x)\)
P17
x是向量的F(x)函数
Now we can apply Newton’s method to: \(x^{[1]} \)= argmin \(F(x)\). Given a current \(x^{(k)}\), we approximate our goal by:
$$ 0=\nabla F( \mathbf{x}) ≈\nabla F (\mathbf{x} ^{(k)})+\frac{∂F ^2(\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} (\mathbf{x−x} ^{(k)}) $$
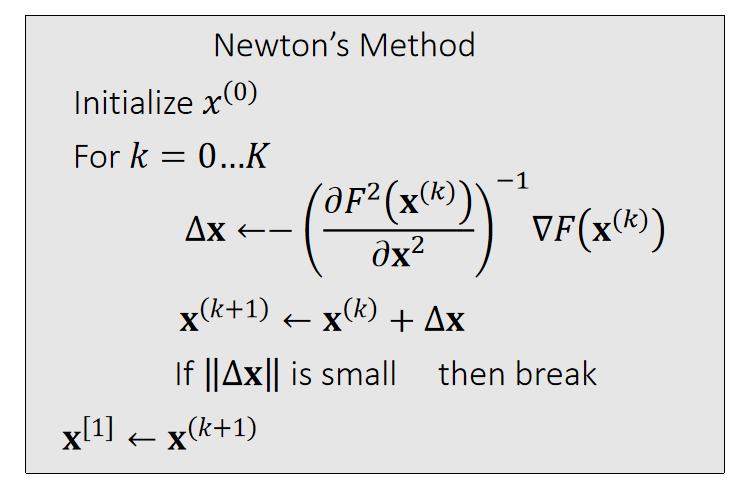
✅ 按照 \(\Delta x\) 的更新公式，只需要用到\(F'(x)\) 和 \({F}''(x)\)， 不需要知道 \(F(x)\).
✅ 此处\(x\)是向量，因此\(F'(x)\)是向量，\({F}''(x)\)是 Hession 矩阵
本文出自CaterpillarStudyGroup，转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/