刚体对外力的响应
虽然刚体受到的力都是作用在刚体上的某个点上。但受力点不能独立的响应这个力。而是要让刚体作为整体来响应这个力。
即，刚体的质心的全局位置（世界坐标系）和全局旋转（世界坐标系）。
因此，刚体在力的作用下会发生旋转和平移。
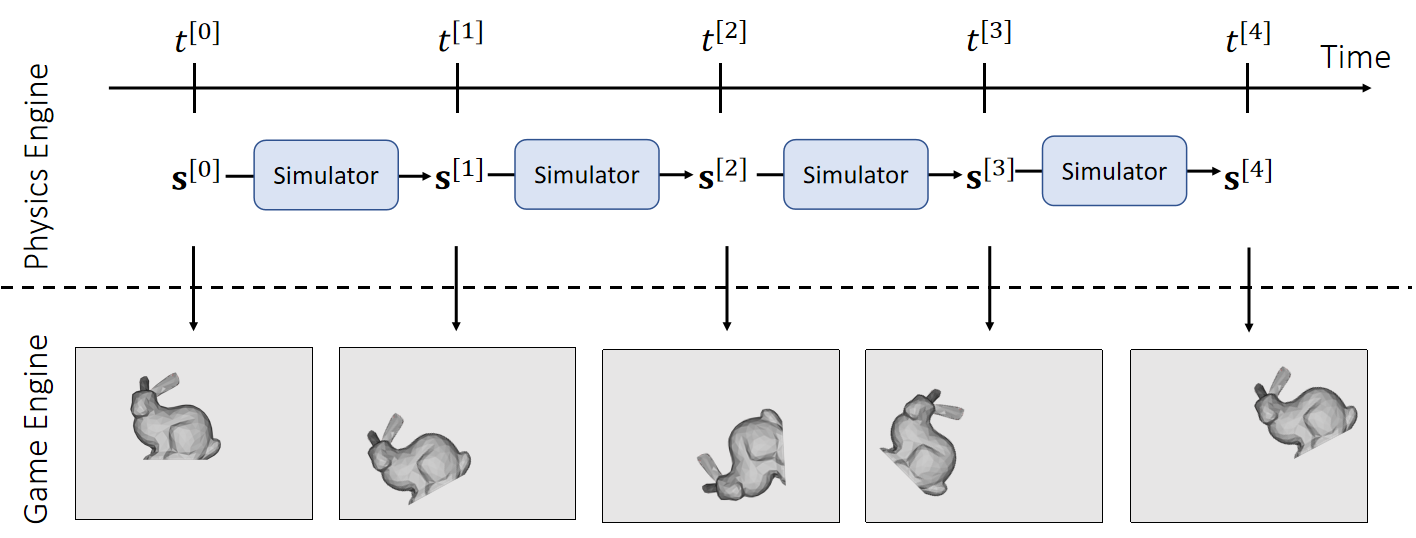
刚体受到经过质心的力
刚体受到经过质心的力，会发生位移，即x的改变。但不会发生旋转。 以下情况可以看作是刚体受到经过质心的力：
- 力作用在刚体的一个或多个点上，且每个力都经过质心
- 对于均质刚体，对整个刚体施加一个力，例如重力
刚体受力后的平移响应与粒子相似。连续形式与离散形式下的速度、位置更新公式也相同。
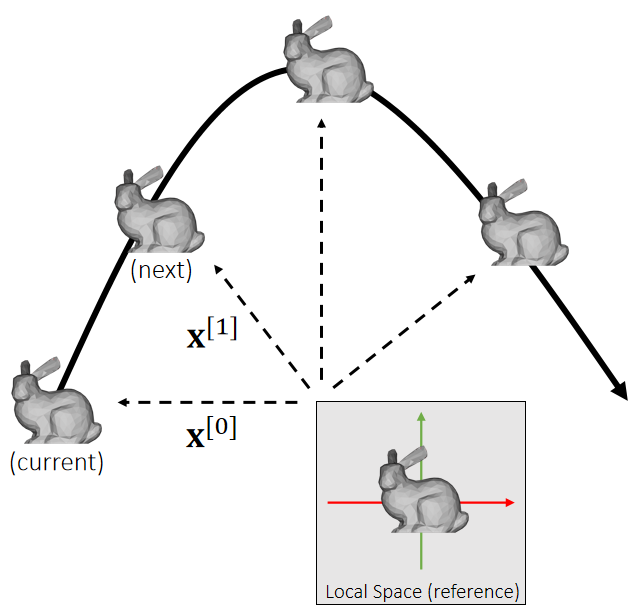
刚体受到一个不经过质心的力
对刚体上的一个点施加一个力F，且力不经过质心，其作用等效于：
- 对刚体的质心施加一个力，其它大小与方向与F相同。这个力导致刚体平移。仿真方法上同一节。
- 对刚体施加一个力偶，其力矩使刚体发生旋转。
inertia、torque等概念，请戳这里link
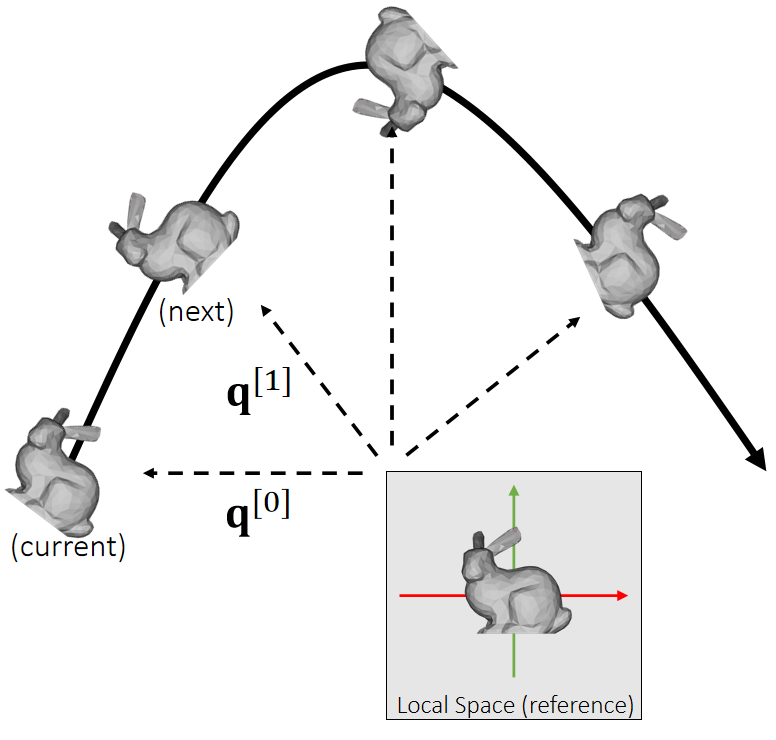
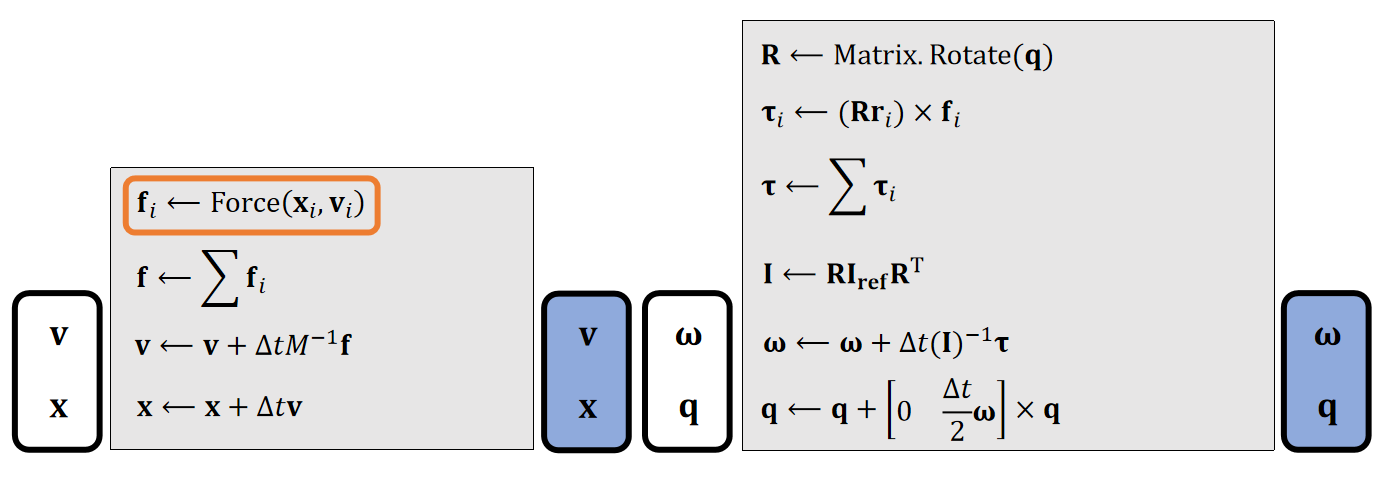
参考刚体平移的离散积分过程，可以推导出刚体旋转的更新法则：
| Translational (linear) | Rotational (Angular) | |
|---|---|---|
| Updafe |  |  |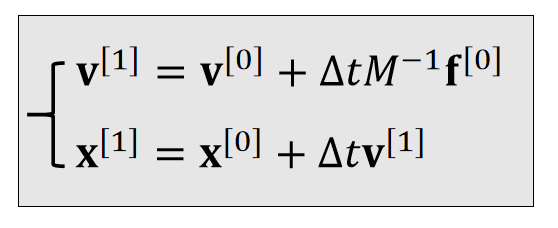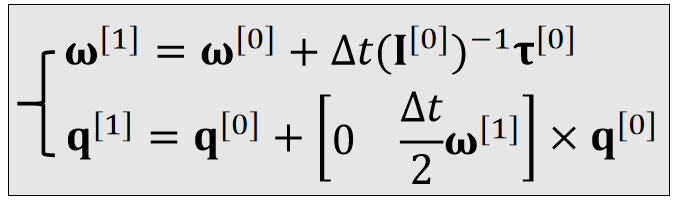
| states | Velocity \(\mathbf{v}\) Position \(\mathbf{x}\) | Angular velocity \(\mathbf{ω} \) Quaternion \(\mathbf{q}\) |
| Physical Quantities | Mass \(\mathbf{M}\) Force \(\mathbf{f}\) | Inertia \(\mathbf{I} \) Torque \(\mathbf{τ} \) |
✅ 平移： \(加速度 = \frac{力}{质量}\) ，旋转： \(加速度 =\frac{力矩}{\text{Inertia}}\)
✅ \(q\)是四元数，代表物体的旋转状态
✅ \(q_1\times q_2\)不是叉乘，而是四元数普通乘法
✅ \(\begin{bmatrix} 0 & \frac{\bigtriangleup t}{2} & w^{(1)} \end{bmatrix}\)是一个四元数，0为实部，后面为虚部
❗ 算完\(q^{[1]}\)的之后要对它 Normalize
🔎 由\(q^{[0]}\)到\(q^{[1]}\)的更新公式的推导过程见Affer Class Reading（Appendix B）
更复杂的情况
更复杂的情况，也都可以把力分解为经过质心的力（造成平移）和力矩（造成旋转）。
计算出力和力矩以后，都可以套用以上公式更新刚体状态。
P30
总结
