P30
Log-Barrier Interior Point Methods
内点法把碰撞解除抽象为带约束优化问题。优化的目标是\(\mathbf{x}^{[0]}→\mathbf{x}^{[1]}\),优化的约束是不碰撞。问题是如何把离散曲面的碰撞检测描述为优化公式?
\(||\mathbf{x}_{ij}||\)就是这个目的。
算法过程
For simplicity, let’s consider the Log-barrier repulsion between two vertices.
$$E(\mathbf{x} )=−\rho \text{ log} ||\mathbf{x} _{ij}||$$
$$ \mathbf{f} _i(\mathbf{x} )=−∇_iE=ρ\frac{\mathbf{x} _ {ij}}{||\mathbf{x} _ {ij}||^2} \\ \mathbf{f} _j(\mathbf{x} )=−∇_jE=−ρ\frac{\mathbf{x} _ {ij}}{||\mathbf{x} _{ij}||^2} $$
[TODO]
$$
\frac{\alpha ||\mathbf{x}|| }{\alpha \mathbf{x}} =\frac{\mathbf{x}^\mathbf{T} }{||\mathbf{x}||}
$$
✅ 用 Log 定义能量、前面某一节课讲过。距离 → 能量 → 斥力
❓ \(||\mathbf{x}_{ij}|| \) 的物理含义没有定义。可能是希望两个三角形之间穿透矩离。\( \mathbf{x}\) 代表两个刚体的状态。
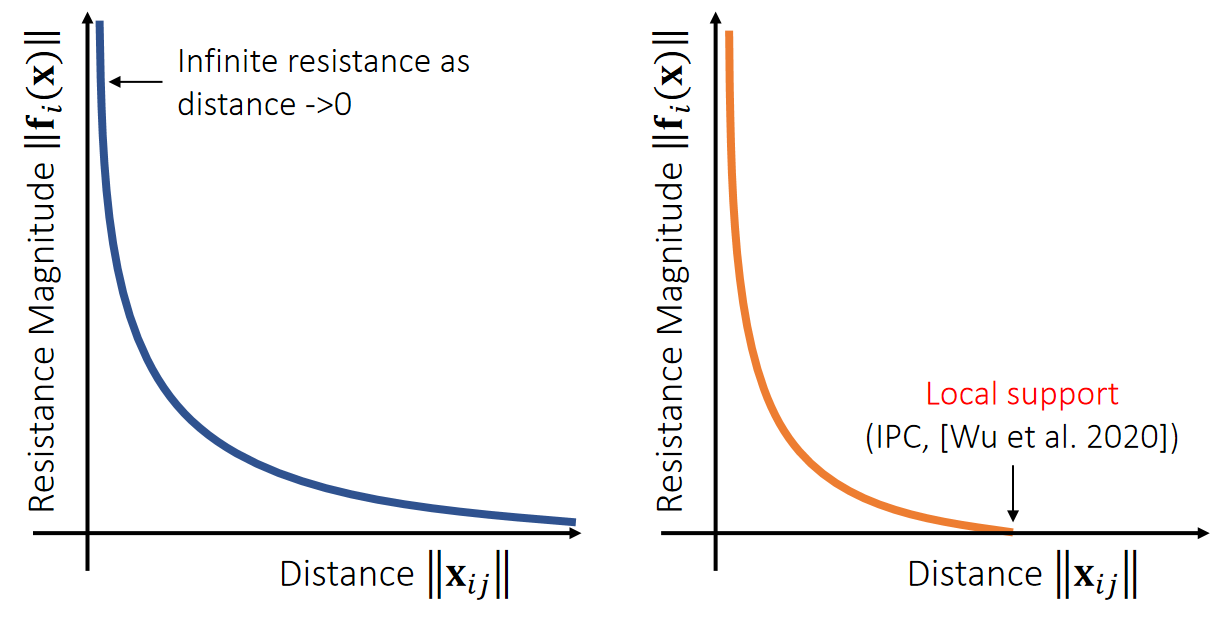
✅ 不需要互斥力一直存在,因此做了一个截断(IPC)
P31
算法实现
We can then formulate the problem as:
$$ \bar{\mathbf{x} }^ {[1]}\longleftarrow \mathrm{argmin} _\mathbf{x} (\frac{1}{2} ||\mathbf{x} −\mathbf{x} ^{[1]}||^2−ρ\sum \mathrm{log} ||\mathbf{x} _{ij}||) $$
✅ 优化目标:点的位置与目标位置(穿模)尽量接近,且不穿模。
✅ 绿色是来自\(\mathbf{x}^{[1]}\)的引力,对应公式第1页。黄色是来自边界的斥力对应公式第2页。
❓ ||\(X_{ij}\)||代表穿模情况,为什么是用距离的方式定义?
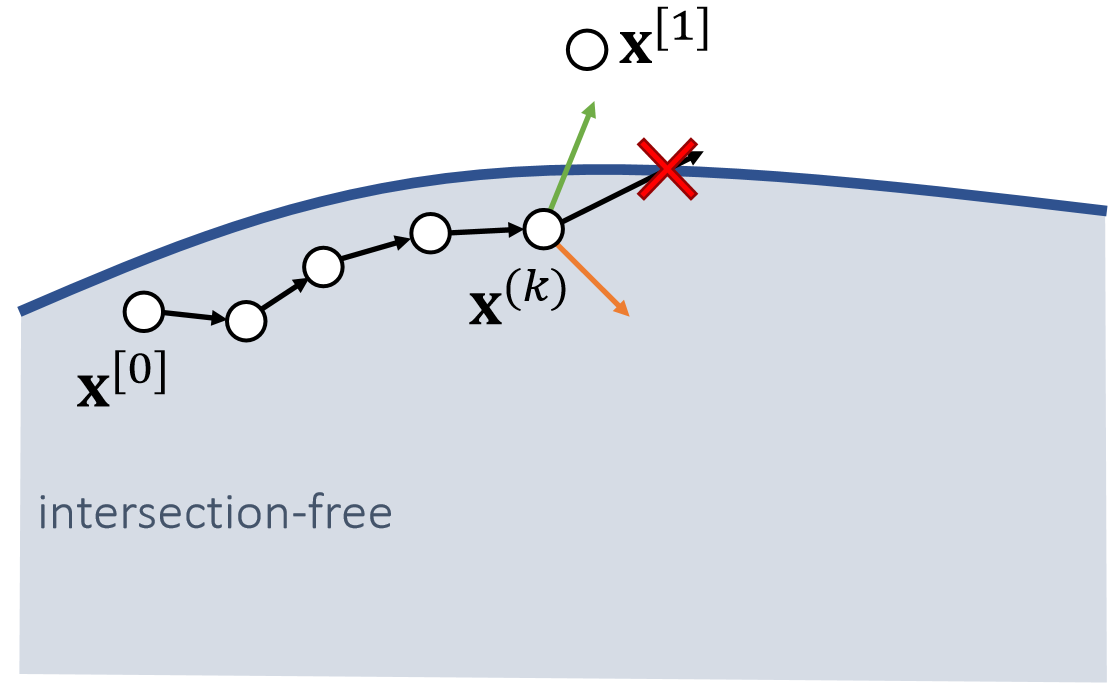
Gradient Descent:
\(\mathbf{x} ^{(0)}\longleftarrow \mathbf{x} ^{[0]}\)
For \(k=0…K\)
$$\mathbf{x} ^{(k+1)}\longleftarrow \mathbf{x} ^{(k)}+α(\mathbf{x} ^{[1]}−\mathbf{x} ^{(k)}+ρ\sum \frac{\mathbf{x} _{ij}}{||\mathbf{x} _{ij}||^2})$$ \(\bar{\mathbf{x} }^ {[1]}\longleftarrow \mathbf{x} ^{(k+1)}\)
✅ 每走一小步都需要反复的碰撞检测,重新计算\(||\mathbf{x} _{ij}||\)。
✅ 关键是步长\(\alpha \)
The step size \({\color{Red} α}\) must be adjusted to ensure that no collision happens on the way. To find \({\color{Red} α}\), we need collision tests.
[❓] \( \alpha \) 不是 learning rate 吗?为什么碰撞检测的结果会影响到\( \alpha \) ?
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/