P22

投影动力学 (Projective Dynamics)

原理

PD VS. 弹簧系统

PD由基于隐式积分弹簧系统演化而来，其基本流程是一致的。

---
title: Projective Dynamics 
---
flowchart LR
    Current(["当前状态"]) 
    Constrain[("约束")]
    Outter[("外力")]
    Energy(["势能能量"]) 
    Mometen(["动能能量"]) 
    Target(["优化目标"])
    Velocity(["速度"]) 
    Next(["下一时刻状态"]) 
    NextWoContrain(["不考虑约束的下一时刻状态"])

    Outter --> Velocity
    Velocity & Current --> NextWoContrain --> Mometen
    Constrain-->Energy 
    Energy & Mometen --> Target --> Optimize --> Next

PD 与弹簧系统的区别在于，弹簧系统与PD计算能量的方式不同。弹簧系统使用弹簧的弹性势能计算能量，而PD使用约束计算能量。能量定义的不同也导致了解优化问题的方法不同。

PD VS. PBD

✅ PBD方法直接拿约束来修复顶点位置，没有物理含义。而Projective Dynatics把projection方法跟物拟模拟结合起来。
✅ Projective Dynamics与PBD的差别主要体现在用约束来做什么。

Projective Dynamics将约束转化为能量，通过最小化能量函数来求解系统的状态。因此是一种基于优化的物理仿真方法

优化目标

用隐式积分做弹簧系统，最终会转化为优化问题：

$$ \Psi(\mathbf{x}) = \frac{1}{2∆t^2}||\mathbf{x} −\mathbf{y}||_\mathbf{M}^2+E(\mathbf{x} ) $$

其中y为显式积分的结果，E(x)为系统的势能。

目标是优化\(\Psi\)：

$$ x = \argmin \Psi(x) $$

在弹簧系统中，这样定义E(x)

$$ E(x) = \sum _ {e=(i,j)}E _ e= \frac{1}{2} k\sum _ {e=(i,j)} (||\mathbf{x} _ {i} − \mathbf{x} _ {j} ||−L _ e)^2 $$

势能能量E(x)

1根弹簧，2个顶点

引入变量p为长度为\(L_e\)的向量：

$$ p = \overrightarrow {\mathbf{x} _ {i}'\mathbf{x} _ {j}'} $$

$$ \begin{aligned} E(x) &= \frac{1}{2} k(||\mathbf{x} _ {i} −\mathbf{x} _ {j} ||−L _ e)^2 \\ &= \min \frac{1}{2} k(||(\mathbf{x} _ {i} − \mathbf{x} _ {j}) - (\mathbf{x} _{i}' −\mathbf{x} _ {j}') ||)^2\\ &= \min \frac{1}{2} k(||(\mathbf{x} _ {i} −\mathbf{x} _ {j}) - p ||)^2 \end{aligned} $$

可以解得：

$$ p = \argmin E(x) = L\frac{x _ i-x _ j}{||x _ i-x _ j||} $$

代入p得：

$$ \begin{aligned} E(x) &= \frac{1}{2} k(||(\mathbf{x} _ {i} −\mathbf{x} _ {j}) - p ||)^2 \\ &= \frac{1}{2} k ( || \underbrace{\begin{bmatrix} I & -I \end{bmatrix}} _ {3 \times 6} \underbrace{\begin{bmatrix} x _ i \\ x _ j \end{bmatrix}} _ {6 \times 1} - \underbrace{p} _ {3\times 1}||^2) \end{aligned} $$

根据牛顿法，需要根据E(x)的一阶导和二阶导来计算x的更新方向：

$$ \begin{aligned} \nabla E &= k \begin{bmatrix} I \\ -I \end{bmatrix} (\begin{bmatrix} I & -I \end{bmatrix} \begin{bmatrix} x_i \\ x_ j \end{bmatrix} - p) && \nabla E \in R^{6\times1}\\ H &= k \begin{bmatrix} I \\ -I \end{bmatrix} \begin{bmatrix} I & -I \end{bmatrix} = k \begin{bmatrix} I & -I \\ -I & I \end{bmatrix} && H \in R^{6\times6} \end{aligned} $$

n根弹簧，m个顶点

引入变量p，其中\(p_ e\)为长度为\(L_ e\)的向量：

$$ p_{e=(i,j)} = \overrightarrow {\mathbf{x} _ {i}'\mathbf{x} _ {j}'} $$

$$ \begin{aligned} E(x) &= \frac{1}{2} k \sum _ {e=(i,j)}(||\mathbf{x} _ {i} −\mathbf{x} _ {j} ||−L _ e)^2 \\ &= \min \frac{1}{2} k\sum _ {e=(i,j)}(||(\mathbf{x} _ {i} −\mathbf{x} _ {j}) - (\mathbf{x} _ {i}' −\mathbf{x} _ {j}') ||)^2\ &= \min \frac{1}{2} k\sum _ {e=(i,j)}(||(\mathbf{x} _ {i} −\mathbf{x} _ {j}) - p_ e ||)^2 \end{aligned} $$

可以解得：

$$ p _ e = \argmin E _ {e=(i,j)}(x) = L\frac{x _ i-x _ j}{||x _ i-x_j||} $$

代入p得：

$$ \begin{aligned} E(x) &= \frac{1}{2} k\sum _ {e=(i,j)}(||(\mathbf{x} _ {i} −\mathbf{x}_{j}) - p_e ||)^2 \\ &= \frac{1}{2} k ( || \underbrace{A} _ {3n \times 3m} \underbrace{\mathbf{x}} _ {3m \times 1} - \underbrace{P} _ {3n\times 1}||^2) \end{aligned} $$

其中，A是由弹簧连接关系构成的矩阵，只要弹簧结构不发生变化，整个仿真过程中A保持炒变。

根据牛顿法，需要根据 \(E(x)\) 的一阶导和二阶导来计算 \(x\) 的更新方向：

$$ \begin{aligned} \nabla E &= k A^T (A \mathbf{x} - P) && \nabla E \in R^{3m\times1}\\ H &= k A^TA && H \in R^{3m\times3m} \end{aligned} $$

说明

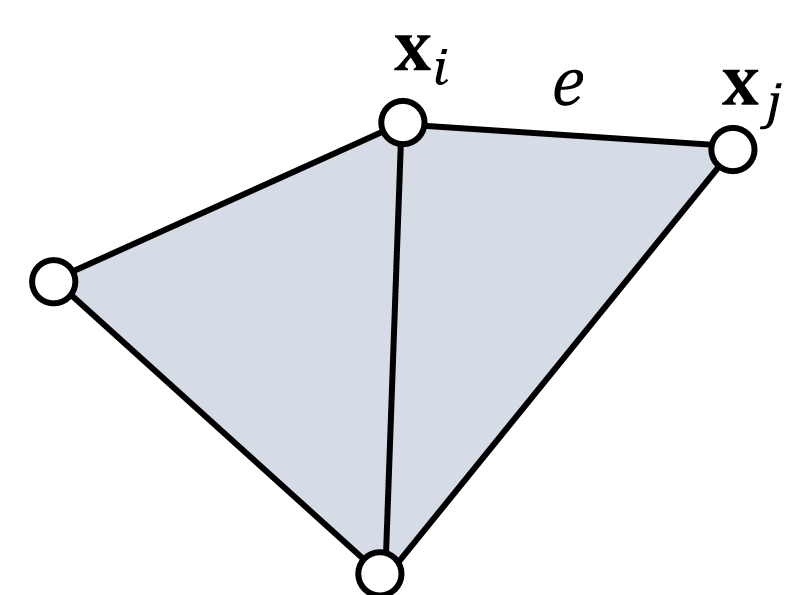
引入的变化p是形变后的e的投影

$$ (\mathbf{x} _ {e,i}^{\mathrm{new} },\mathbf{x} _ {e,j}^{\mathrm{new} }) = \mathrm{Projection} _ e(\mathbf{x} _ i,\mathbf{x} _ j) $$

✅ 本文基于约束定义能量。{\(\mathbf{x} _{e,i}^{\mathrm{new} },\mathbf{x} _ {e,j}^{\mathrm{new} }\)}为期望的顶点位置。不直接把顶点从当前位置移到期望位置。而是把当前位置和期望位置的距离转化为能量，通过能量推动顶点从当前位置移到目标位置。

因此称为投影动力学

这个能量与弹簧能量有什么区别

$$ E(\mathbf{x})=\sum {e=(i,j)}\frac{k}{2}(||\mathbf{x} i-\mathbf{x}_j||-L _ e)^2 $$

$$ \mathbf{f} _ i=−\nabla_iE(\mathbf{x} )=−{\textstyle \sum _{e:i\in e}}(\mathbf{x} _ i−\mathbf{x} _ j)−(\mathbf{x} _ {e,i}^{\mathrm{new}} −\mathbf{x} _ {e,j}^{\mathrm{new} }) $$

✅ 基于 \(E(\mathbf{x})、\mathbf{x}_i^{\mathrm{new} } 、\mathbf{x} _ j^{\mathrm{new} }\) 计算力，此时假设\(\mathbf{x} _ i^{\mathrm{new} }\)和 \(\mathbf{x} _ j^{\mathrm{new} }\)都是定值，\(\mathbf{x} _ i\)和 \(\mathbf{x} _ j\)是变量。
✅ 本文基于约束定义能量和力，得到的结果与基于弹簧能量计算的能量和力相同。
✅ 既然 \(E\) 和 \(F\) 是一样的，何必多此一举? 答：H不同。

P23

Hessian 矩阵

Instead of blending projections in a Jacobi or Gauss-Seidel fashion as in PBD, projective dynamics uses projection to define a quadratic energy.

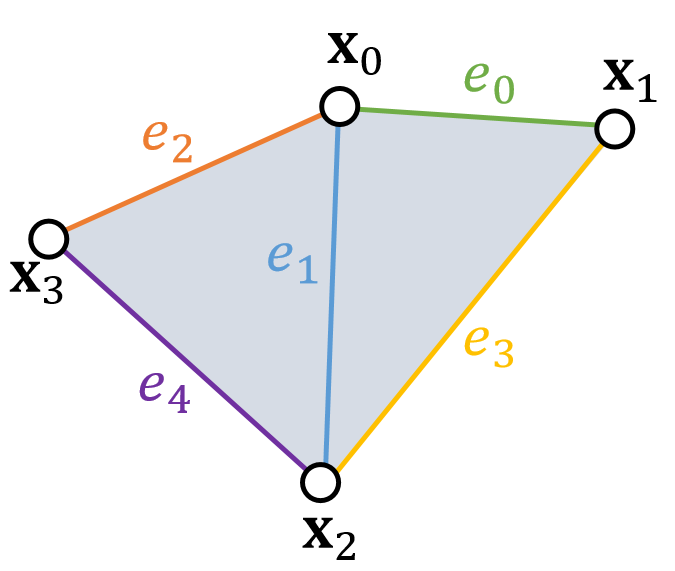
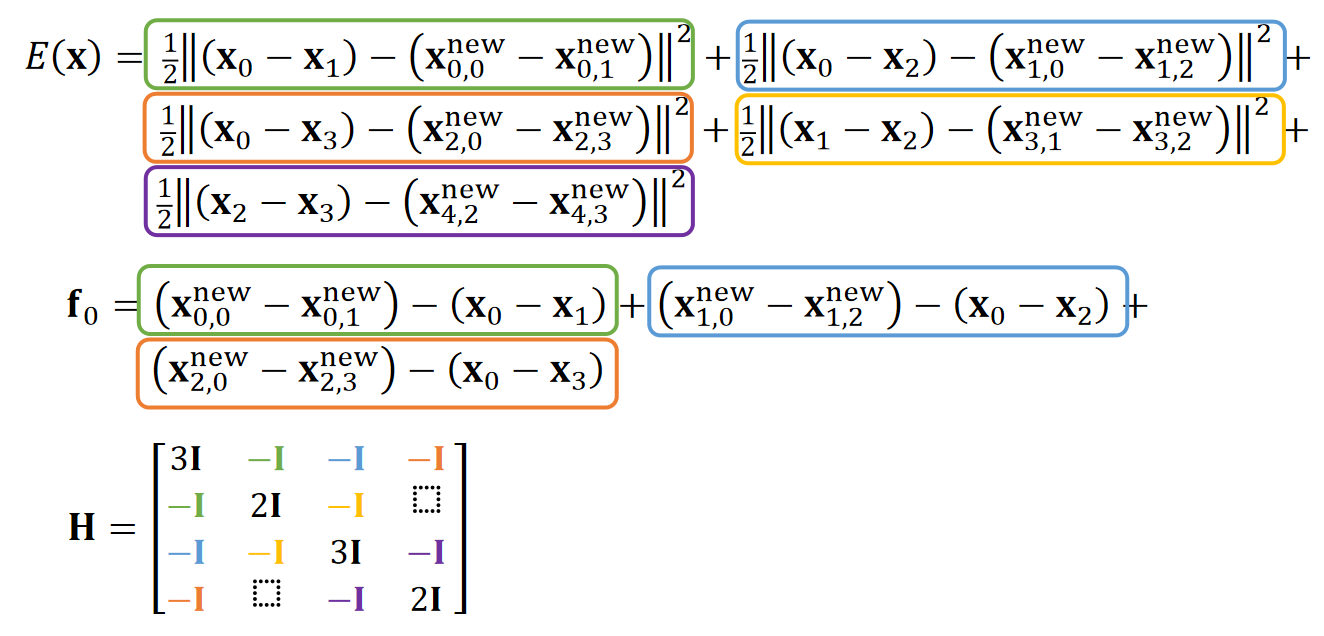
✅ 同一个顶点在三个不同边上的投影是不同的。
✅ 可以直接根据Mesh的拓扑关系构造H矩阵。
✅ 为什么能简化\(\mathbf{H}\)的计算？答：在计算某一个端点时，假设另一个端点不动（常量），那么能量就是只关于这个端点的二次函数

为什么这样定义能量

以这种方式定义能量，得到的H是一个只与弹簧拓扑有关的定值。这个定值不光构造简单，也能简化计算。

在以牛顿法的优化迭代方法中，需要解线性系统\(Ax=b\)。复杂的A使得线性系统难以求解。

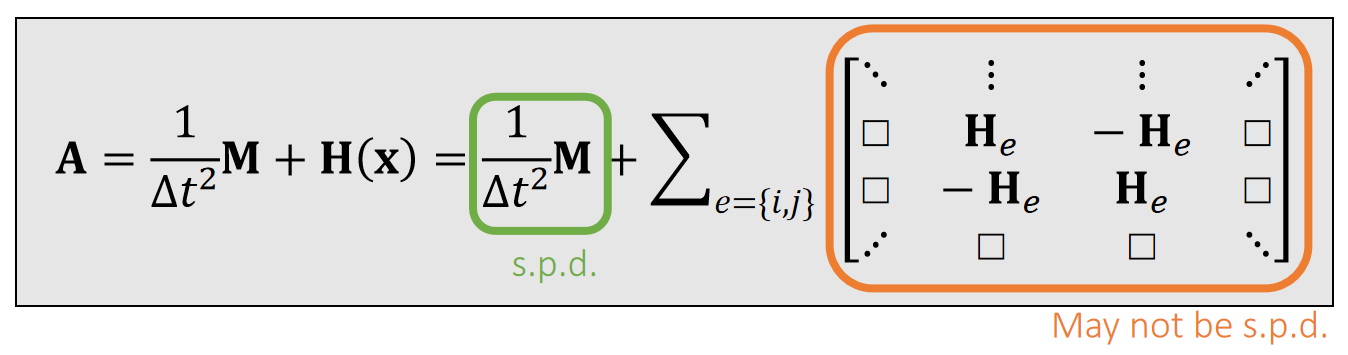
由A的定义可知，当H是定值时，A也是一个定值。那么可以对A做一些预计算，以加速线性系统\(Ax=b\)的求解。

如果只是使用了PD的方法来构造能量和H，但没有对A做预计算，实际上没有发挥PD的核心优势。

P28

After-Class Reading

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/