P23

Boundary Conditions

Dirichlet boundary

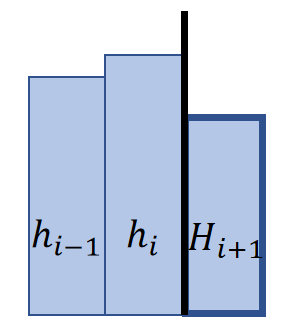
A Dirichlet boundary assumes that the boundary height $H_{i+1}$ is constant. It’s considered as an open boundary.

$$ℎ_{i+1}−ℎ_i+ℎ_{i−1}−ℎ_i=H_{i+1}−ℎ_i+ℎ_{i−1}−ℎ_i$$

✅ 这种方法用于模拟开放的水面，例如大海的区域、假设被模拟的区域外是静止的水面、高度为常数，(Dirichlet)
✅ $h$为边界内，$H$为边界外。

P25

Algorithm with Neumann Boundaries

Extending the simulator to 3D is also straightforward.

Neumann boundary

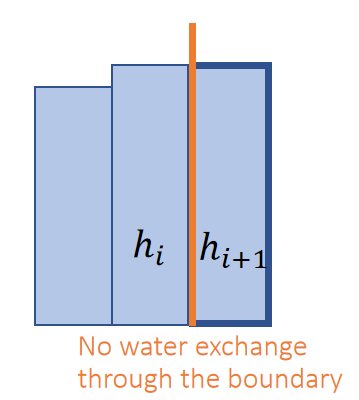
A Neumann boundary specifies the boundary derivatives. For example, a zero-derivative boundary means $ℎ_{i+1}≡ℎ_i$. It’s considered as a closed boundary.

$$ℎ_{i+1}−ℎ_i+ℎ_{i−1}−ℎ_i=ℎ_{i−1}−ℎ_i$$

✅ Neuman 用于模拟有边界水域，例如池堂、假设边界上没有水流交换。

P24

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/