P14
Strain Limiting
PBD 是一个让仿真结果变得满足约束的方法,可以认为是仿真的后处理。由此产生了其它的用法。
原理
Strain limiting aims at using the projection function for correction only.
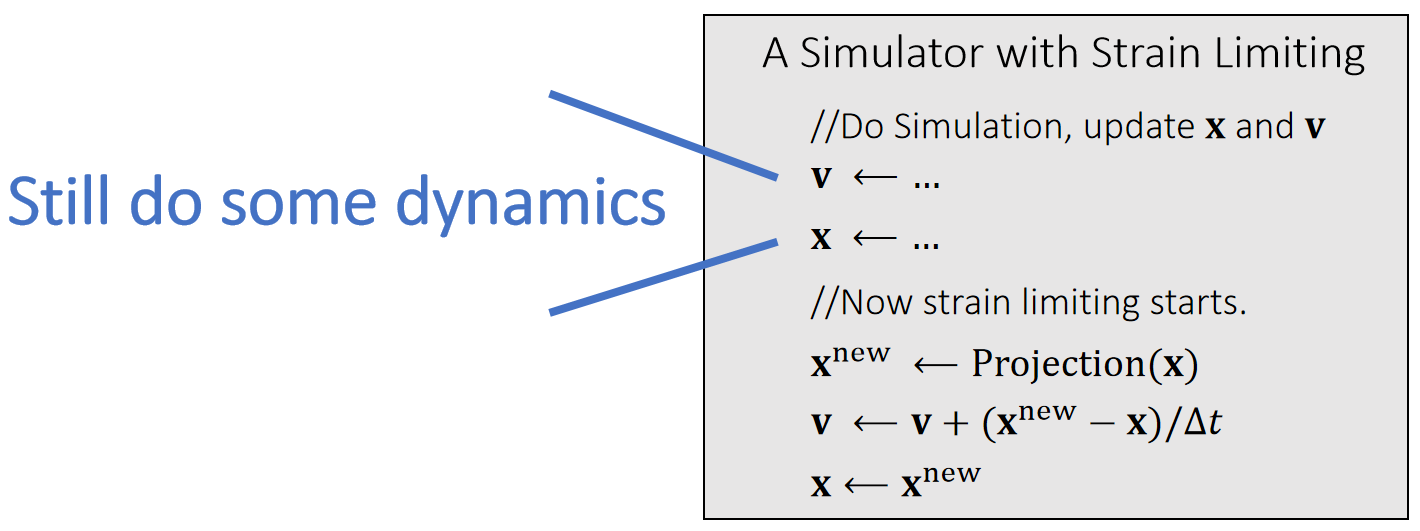
✅ 投影函数作为模拟过程的后处理,防止模拟后产生大的形变,使模拟结果更稳定。
| PBD | Strain Limiting | |
|---|---|---|
| 第一步 | 只考虑粒子运动,不考虑约束 | 模拟粒子运动、同时考虑约束 |
| 第二步 | 使粒子状态满足约束 | 校正,但约束较宽 |
P15
例一: Spring Strain Limit
We can set the spring strain, i.e., the stretching ratio σ, to be within a limit.
✅ 这一页以弹簧为例子说明 Strain Limit
✅ Strain:物理上描述形变的量,即本页的\(\sigma \)
$$ \sigma ^\mathrm{{min}}≤\frac{1}{L}||\mathbf{x} _i− \mathbf{x} _j||≤\sigma^\mathrm{{max}} $$
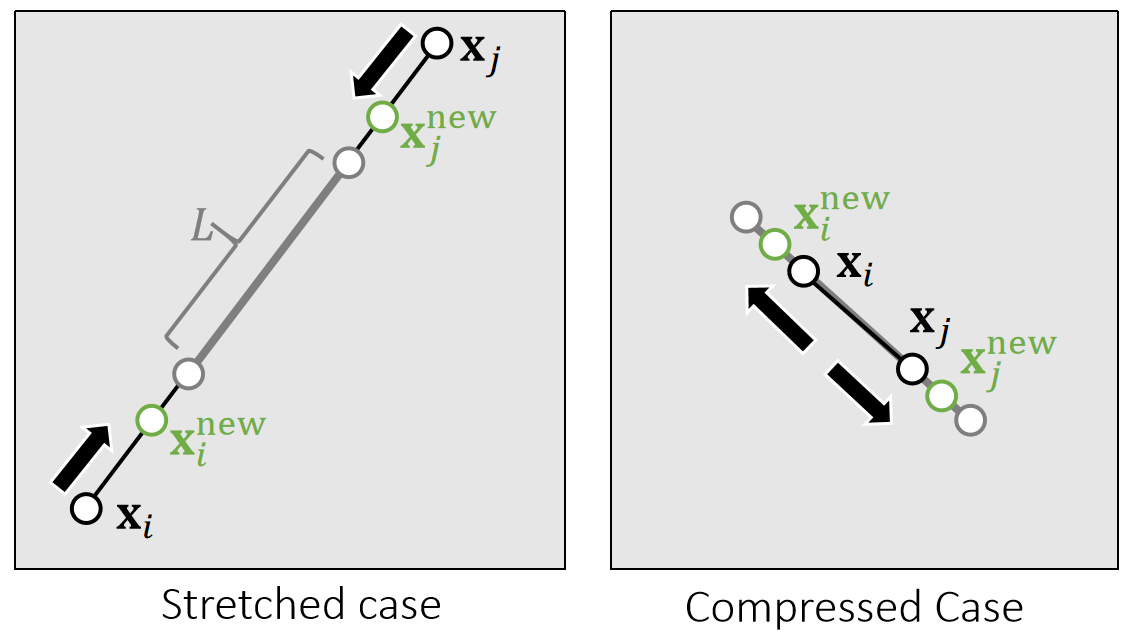
✅ 仅要求弹簧长度满足某不比例,不要求一定到达某个位置。
Constraint
P16
$$ \quad $$
$$ \mathbf{x}^{\mathbf{new}}\longleftarrow \mathrm{Projection} (\mathbf{x} ) $$
$$ \sigma\longleftarrow \frac{1}{L}||\mathbf{x}_i− \mathbf{x}_j|| $$
✅ 计算当前拉伸比
$$ \sigma _0\longleftarrow \mathrm{min} (\mathrm{max} (\sigma,\sigma^{\mathrm{min} }),\sigma^{\mathrm{max} }) $$
✅ 计算期望的拉伸比
$$ \mathbf{x} _i^{\mathrm {new} }⟵\mathbf{x} _i−\frac{m_j}{m_i+m_j}(||\mathbf{x} _i− \mathbf{x} _j||−σ_0L)\frac{\mathbf{x} _i− \mathbf{x} _j}{||\mathbf{x} _i− \mathbf{x} _j||} $$
$$ \mathbf{x} _j^{\mathrm {new} }⟵\mathbf{x} _j+\frac{m_j}{m_i+m_j}(||\mathbf{x} _i− \mathbf{x} _j||−σ_0L)\frac{\mathbf{x} _i− \mathbf{x} _j}{||\mathbf{x} _i− \mathbf{x} _j||} $$
✅ 用\(\sigma _0L\)代替原长\(L\).
\(\mathrm{PBD}: \sigma _0≡1;\quad\quad\)
✅ PBD可以看作是Strain Limit的特例。
No limit: \(\sigma ^{\mathrm{min} } = 0, σ^{\mathrm{max} } = \infty\)
✅ Strain Limit 的应用场景:(1) 模拟布料:“拉伸到一定范围后变得非常 stiff” 的效果 (2) 防止“形变大发生数值不稳定”。
P17
例二:Triangle Area Limit
We can limit the triangle area as well. To do so, we define a scaling factor.
✅这是另一个例子。希望顶点移动尽量少,因此定义约束:三角形面积变化在一定范围内。
{\(\mathbf{x}_i^{\mathrm{new} },\mathbf{x}_i^{\mathrm{new} },\mathbf{x}_k^{\mathrm{new} }\)} = \(\mathrm{argmin} \frac{1}{2} \){\(m_i||\mathbf{x}_i^{\mathrm{new} }−\mathbf{x}_i||^2+m_j||\mathbf{x}_j^{\mathrm{new} }−\mathbf{x}_j||^2+m_j||\mathbf{x}_k^{\mathrm{new} }−\mathbf{x}_k||^2\)}
such that the constraint is satisfied.
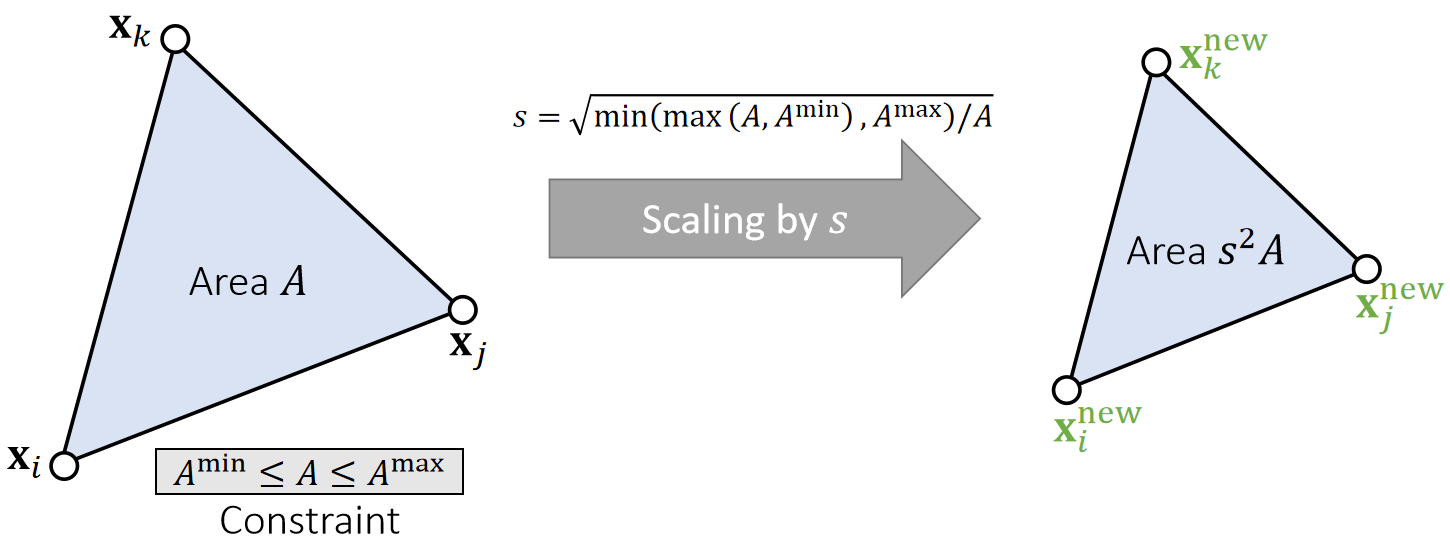
✅ strain s为面积的缩放量
P18
$$ \quad $$
$$ \mathbf{x} ^{\mathbf{new}} ⟵\mathrm{Projection} (\mathbf{x} ) $$
$$ \mathbf{A}\longleftarrow \frac{1}{2} ||(\mathbf{x} _j− \mathbf{x} _i)\mathbf{×} (\mathbf{x}_k− \mathbf{x} _i)|| $$
✅ 计算当前三角形的面积
$$ \mathbf{s} \longleftarrow \sqrt{\mathrm{\mathrm{min}} (\mathrm{\mathrm{max}} (A,A^{\mathrm{min}}),A^{\mathrm{max}})/A} $$
✅ 计算期望的面积缩放比
$$ \mathbf{c} \longleftarrow \frac{1}{m_i+m_j+m_k} (m_i\mathbf{x} _i+m_j\mathbf{x} _j+m_k\mathbf{x} _k) $$
✅ C为质心,要求缩放前后质心不变。数学上、质心不变,点的移动最少;物理上,质心变了代表物体运动了,scale 不应该导致物理运动。
$$ \mathbf{x} _i^{\mathrm{new}}\longleftarrow \mathbf{c} +s(\mathbf{x} _i−\mathbf{c} ) $$
$$ \mathbf{x} _j^{\mathrm{new}}\longleftarrow \mathbf{c} +s(\mathbf{x} _j−\mathbf{c} ) $$
$$ \mathbf{x} _k^{\mathrm{new}}\longleftarrow \mathbf{c} +s(\mathbf{x} _k−\mathbf{c} ) $$
✅ 通过对顶点到质心的距离的缩放,得到顶点的新的位置
P19
Strain Limiting在Simulation中的作用
-
Strain limiting is widely used in physics- based simulation, typically for avoiding instability and artifacts due to large deformation.
-
Strain limiting is useful for nonlinear effects, in a biphasic way.

✅ 例如布料一般一开始抵抗比较小,拉到一定程度后抵抗迅速变大。对这种非线性的表现,可以把模拟分布两个阶段,前面用普通模拟,后面用strain limiting。
- Strain limiting also helps address the locking issue.
✅两个阶段有不同的算法,针对两个阶段的不同特点,可以分别解决两个阶段的问题。
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/