P14
- Intuitively, they represent the flow speed between two cells. For example, we write the volume changing speed at cell (i,j) as:
| $$u_{i+1,j}+v_{i,j+1}−u_{i,j}−v_{i,j}$$ |
|---|
✅ 通过四面墙上的速度计算当前格子的净流出(注意正负号)
P15
Divergence-Free Condition
No volume change is equal to say the fluid is incompressible. This can be formally written as a divergence-free velocity field.
✅ 由于流体不可压,当有流出时,就会产生使等量流入反生的内力。反之亦然。导致最终的趋势是净流入流出为0。
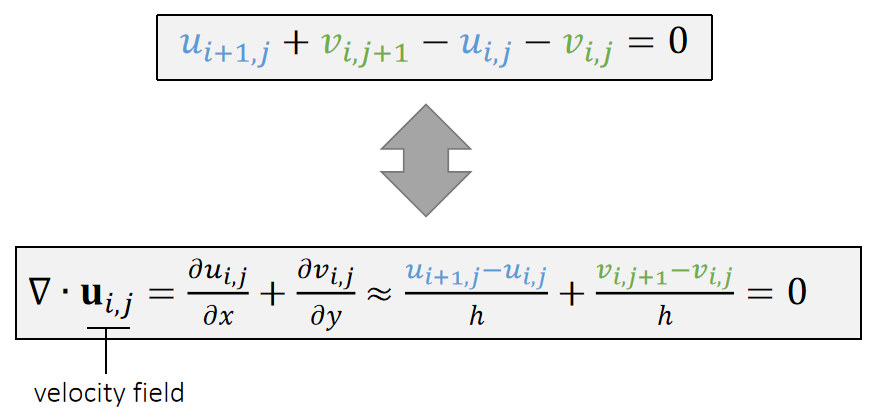
✅ \(\nabla\)为散度符号,见前面课程。
✅ 公式1为直观理解,公式2为数学推导,本质上是一致的。
P16
Bilinear Interpolation
通过微分和差分,可以计算特定点位置的物理属性。再通过插值,计算出任意位置的物理属性。
P17
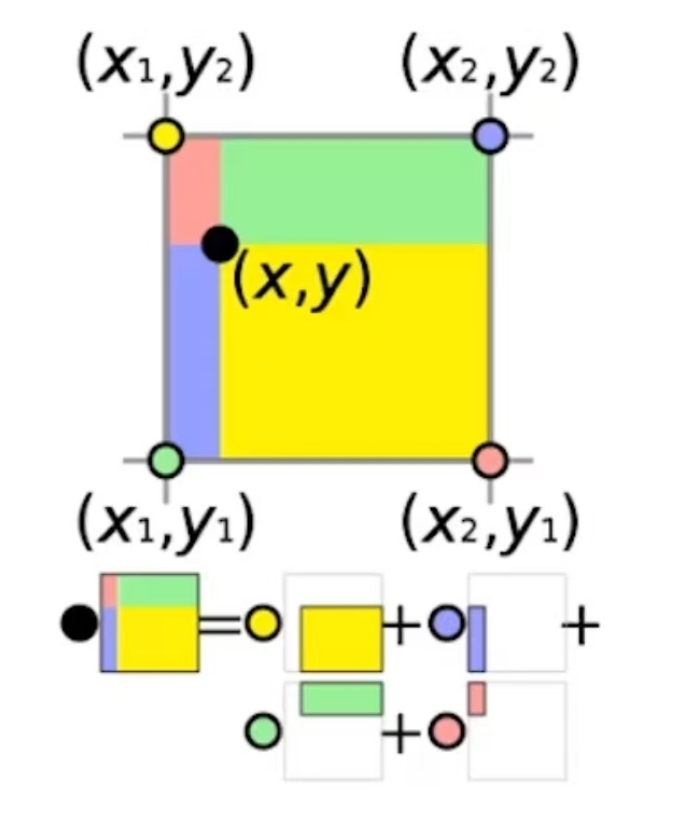
🔎 双线性插值:见GAMES 101
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/