P23

Rigid Body Collision Detection

When the body is made of many vertices, we can detect its collision by testing each vertex

✅ 遍历 mesh 上的每个点，依次做碰撞检测。

No a perfect solution, but acceptable (will come back to this weeks later…)

P24

Rigid Body Collision Response

刚体碰撞响应与粒子碰撞响应的区别

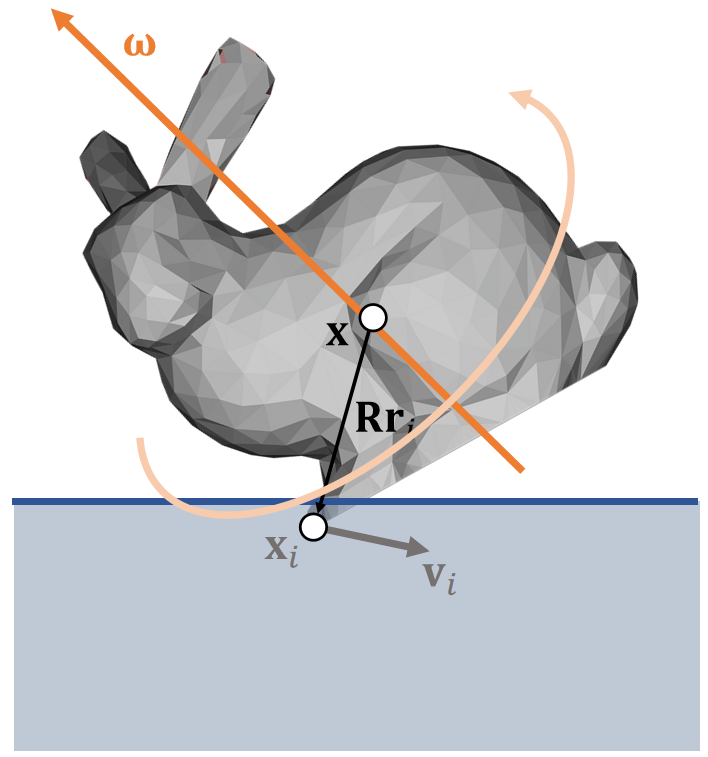
以Vertex i为例，先分析i当前的位置和速度:

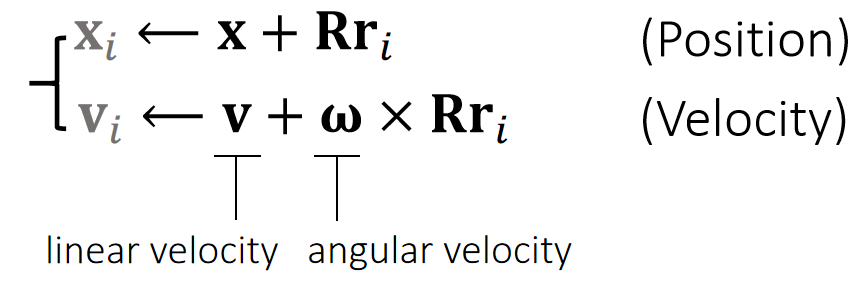
Problem: we cannot directly modify \(\mathbf{x}_i\) or \(\mathbf{v}_i\) isince they not state variables. They areindirectly determined.

✅\(x\)和\(v\)分别是刚体质心点的位置和速度,第二项为刚体上的特定点相对于质心点的位置和速度
对于粒子，可以直接用Impulse修改\(x\)和\(v\)
对于刚体，impulse只能修改\(x\)和\(v\)，不能修改\(x_i\)和\(v_i\)；其中\(x\)可以通过直接修改更新，也可以通过修改\(v\)来更新，这里选择后者。

Solution: we will find a way to modify \(\mathbf{v}\) and \(\mathbf{\omega}\).

✅ 解决方法：通过修改\(\mathbf{v}\)和\(\mathbf{\omega}\)实现修改\(x_i\)和\(v_i\)

P25

反向思考

What happens to \(\mathbf{v}_i\) when an impulse \(\mathbf{j}\) is appliedat vertex \(i\)?

✅ \(\mathbf{j}\) 是一个未知的冲量。\(\mathbf{v}_i\) 是点速度、\(\mathbf{v}\)是线速度
✅假设：此时对\(x_i\)点施加冲量\(j\)，会发生什么？

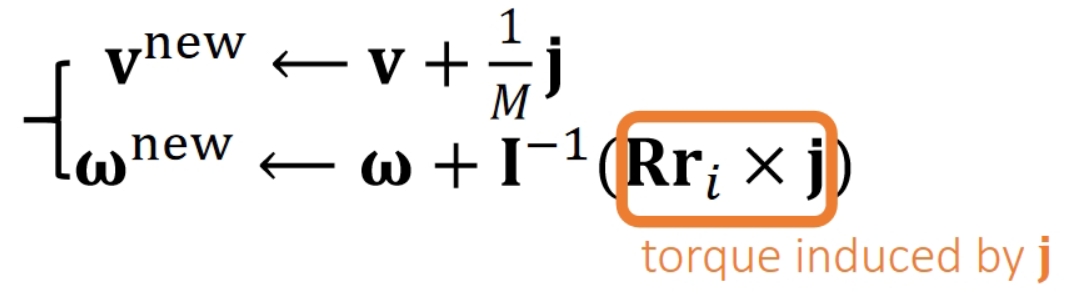
✅ 冲量 = \(Ft\) = \(m\Delta v \Rightarrow \Delta v\) = 冲量/\(m\)，由此得到\(v^{new}\)
✅ 冲量=时间 \(\cdot\)力 = 质量矩阵 * 时间 = 力矩 * t，省略公式中的时间，可得： \(Rr_i \times j\) = 冲量造成的力矩 ＝ 质量矩阵 · \(\Delta \omega \Rightarrow \Delta \omega\) ＝ 质量矩阵\(^{-1}\) · 力矩 ，由此得到\(\omega^{new}\)
❓ 为什么质量矩阵是单位阵？
✅ 由线速度\(v^{new}\)得到点速度\(\mathbf{v}_i^{new}\)

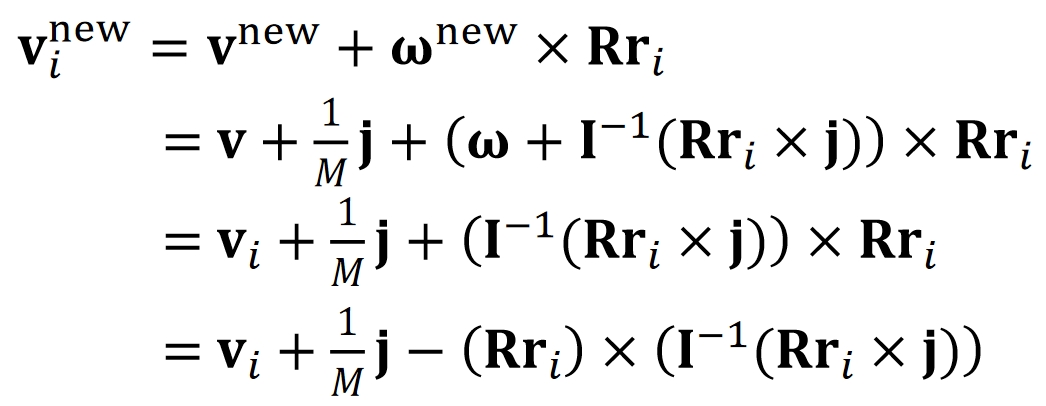
P27

$$ \mathbf{v_i^{new}} = \mathbf{v} _i+\frac{1}{M}\mathbf{j} −(\mathbf{Rr} _i)×(\mathbf{I} ^{−1}(\mathbf{Rr} _\mathbf{i}\times \mathbf{j} )) $$

$$ \mathbf{v_i^{new}} = \mathbf{v} _i+\frac{1}{M} \mathbf{j} −(\mathbf{Rr} _i)^∗\mathbf{I} ^{−1} (\mathbf{Rr} _i)^∗\mathbf{j} $$

✅ 向量之间的点乘可以转化为矩阵与向量的乘法，方便化简。具体内容见页面最后的补充1

化简得：

$$ \mathbf{v_i^{new}}-\mathbf{v}_i=\mathbf{Kj} $$ $$ \mathbf{K} \longleftarrow \frac{1}{M} \mathbf{1} −(\mathbf{Rr} _i)^{∗}\mathbf{I} ^{−1}(\mathbf{Rr} _i)^{∗} $$

✅ 结论，当碰撞点\(i\)确定时，冲量\(j\)和其造成的速度改变量\(Δv\)是确定的，这样，可以通过施加\(j\)，精确修改\(v_i\)
✅ 已知 \(\mathbf{v}_i^{new},\mathbf{v}_i,\mathbf{K}\),可求得 \(\mathbf{j}\)

P28

Rigid Body Collision Response by Impulse

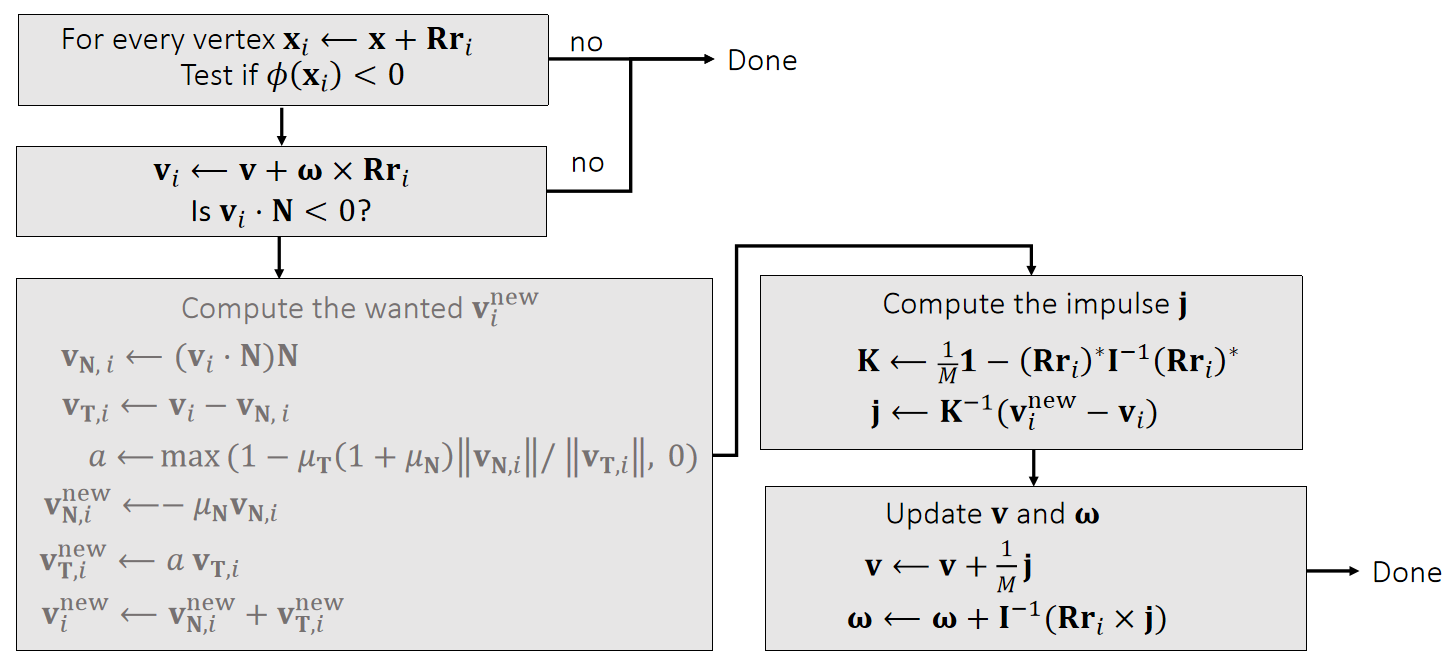
✅ i点发生碰撞 -> 算出i点碰撞后的速度 -> 算出给i点什么样的冲量能让i出现碰撞后的效果 -> 真的施加这样一个冲量 -> 更新刚体状态

P29

Some Implementation Details

  • If there are many vertices in collision, we use their position average.

✅ 如果有多个顶点发生碰撞呢？ 答：方法1，问题简化，用平均值。方法2，解线性系统，见下一页

  • We can decrease the restitution \(\mathbf{\mu_N} \) to reduce oscillation（抖动）.

✅ 抖动原因：重力让它往下，冲量让它往上，导致在地面上反复振荡
解决方法：接近静止时衰减 \(\mathbf{\mu_N} \)

  • We don't update the position here. Why?
    • Because the problem is nonlinear.
    • We will come back to this later when we talk about constraints.

P30

多碰撞点场景

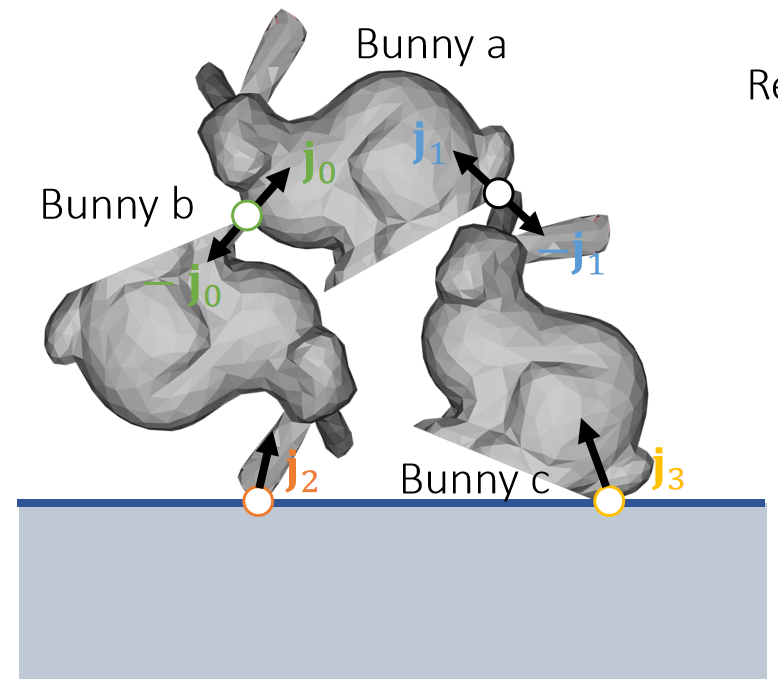
Relative velocity at joints

$$ \begin{cases} \mathbf{v} _0 ^{\mathbf{new} }− \mathbf{v} _0=\mathbf{K} _{a00 }\mathbf{j} _0+\mathbf{K} _{a01 }\mathbf{j} _1 −(−\mathbf{K} _{b00 }\mathbf{j} _0 +\mathbf{K} _{b02}\mathbf{j} _2 )\\ \mathbf{v} _1 ^{\mathbf{new} }− \mathbf{v} _1=\mathbf{K} _{a10 }\mathbf{j} _0+\mathbf{K} _{a11 }\mathbf{j} _1 −(−\mathbf{K} _{c11 }\mathbf{j} _0 +\mathbf{K} _{c13 }\mathbf{j} _3 )\\ \mathbf{v} _2 ^{\mathbf{new} }− \mathbf{v} _2=\mathbf{K} _{b20 }\mathbf{j} _0+\mathbf{K} _{b22 }\mathbf{j} _2\\ \mathbf{v} _3 ^{\mathbf{new} }− \mathbf{v} _3=\mathbf{K} _{c31 }\mathbf{j} _1+\mathbf{K} _{c33 }\mathbf{j} _3 \end{cases} $$

$$ \Downarrow $$

$$ \begin{bmatrix} \mathbf{K} _{a00 }+\mathbf{K} _{b00 } & \mathbf{K} _{a01 } & -\mathbf{K} _{b02 } & \Box \\ \mathbf{K} _{a10 } & \mathbf{K} _{a11 }+\mathbf{K} _{c11 } & \Box & -\mathbf{K} _{c13 }\\ -\mathbf{K} _{b20 } & \Box & \mathbf{K} _{b22} & \Box \\ \Box & -\mathbf{K} _{c31 } & \Box & \mathbf{K} _{c33 } \end{bmatrix}\begin{bmatrix} \mathbf{j} _{0 }\\ \mathbf{j} _{1}\\ \mathbf{j} _{2}\\ \mathbf{j} _{3} \end{bmatrix}=\begin{bmatrix} \bigtriangleup \mathbf{v} _{0}\\ \bigtriangleup \mathbf{v} _{1}\\ \bigtriangleup \mathbf{v} _{2}\\ \bigtriangleup \mathbf{v} _{3} \end{bmatrix} $$

\(\mathbf{K} _{a01}\mathbf{j} _1\) stands for the velocity change of bunny \(a\) at joint 0, caused by impulse \(\mathbf{j}_1\).

P31

After-Class Reading (Before Collision)

https://graphics.pixar.com/pbm2001
Rigid Body Dynamics

P32

Shape Matching

✅ 用粒子的方法来解决刚体的问题

P33

Basic Idea

We allow each vertex to have its own velocity, so it can move by itself.

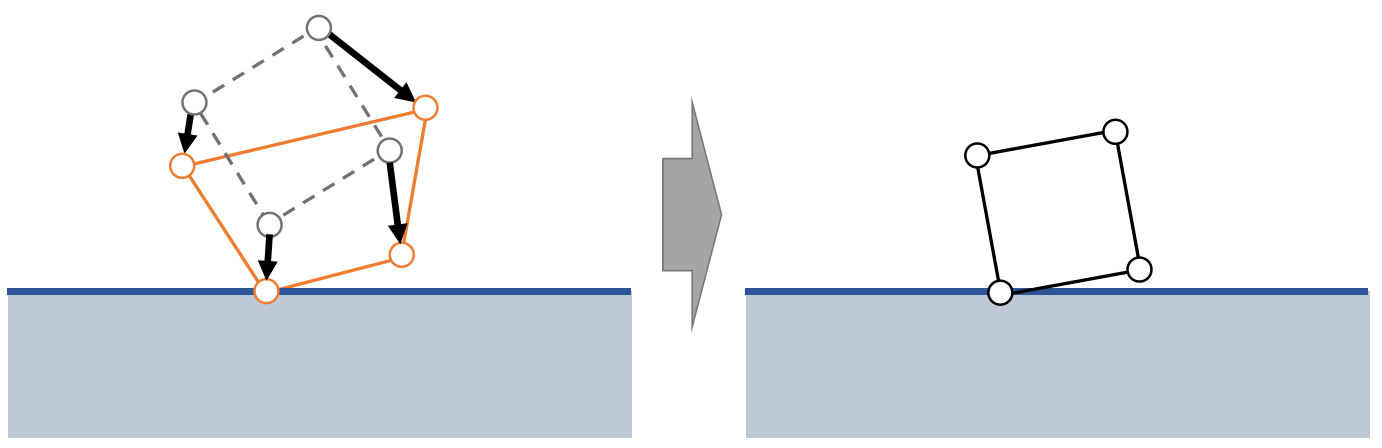
First, move vertices independently by its velocity, with collision and friction being handled.

Second, enforce the rigidity constraint to become a rigid body again.

✅ 第二步是 Shape Matching 的关键

Rigidity

P34

更新质心位置

Now \(\mathbf{c}\) and \(\mathbf{R}\) are unknowns we want to find out from:

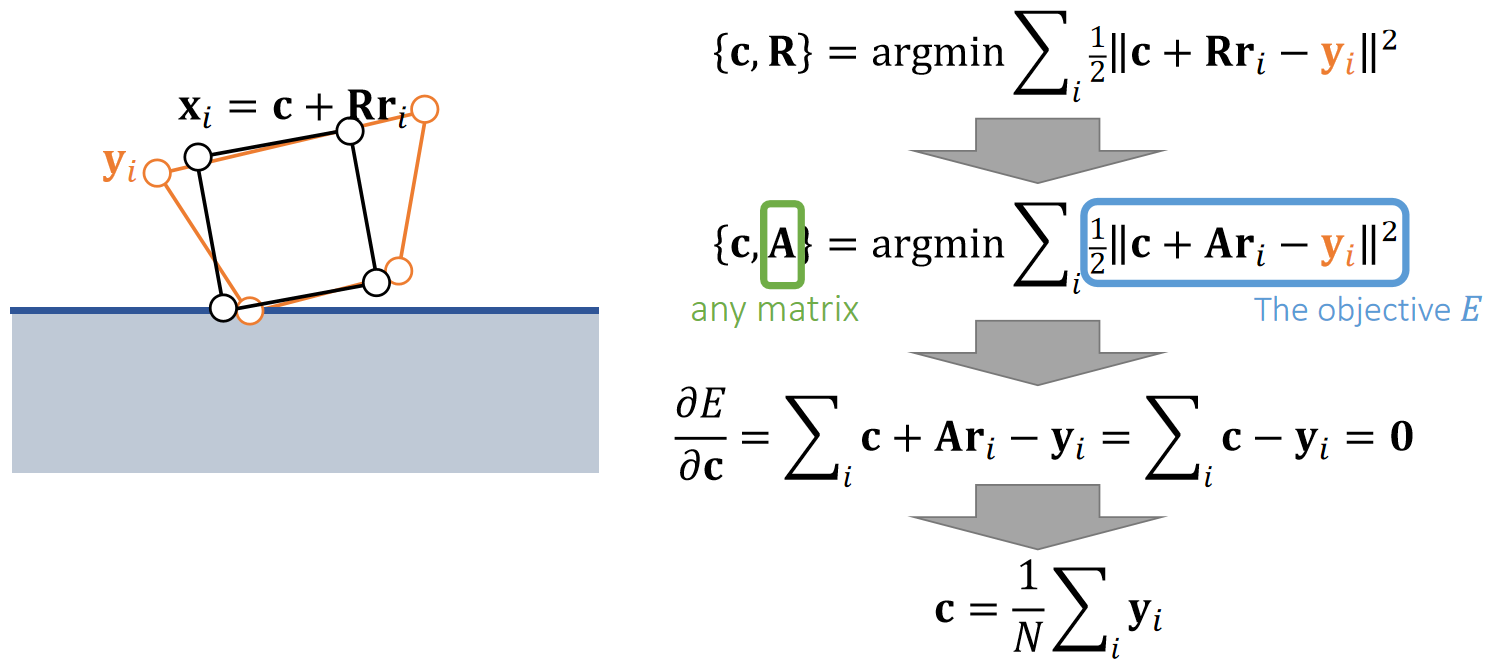
✅ \(\mathbf{c}\) 代表质心，即前面的 \(\mathbf{x}\)
✅ 约束：新的顶点位置与原顶点位置的距离尽量接近。
✅问题简化：用任意矩阵A代替需要满足旋转矩阵约束的\(R\)。因此\(\sum Ar_i = A \sum r_i = 0\)
✅结论：约束前后质心位置不变
❓ 优化之后的刚体可能还是与地面穿透的。

P35

更新质量速度

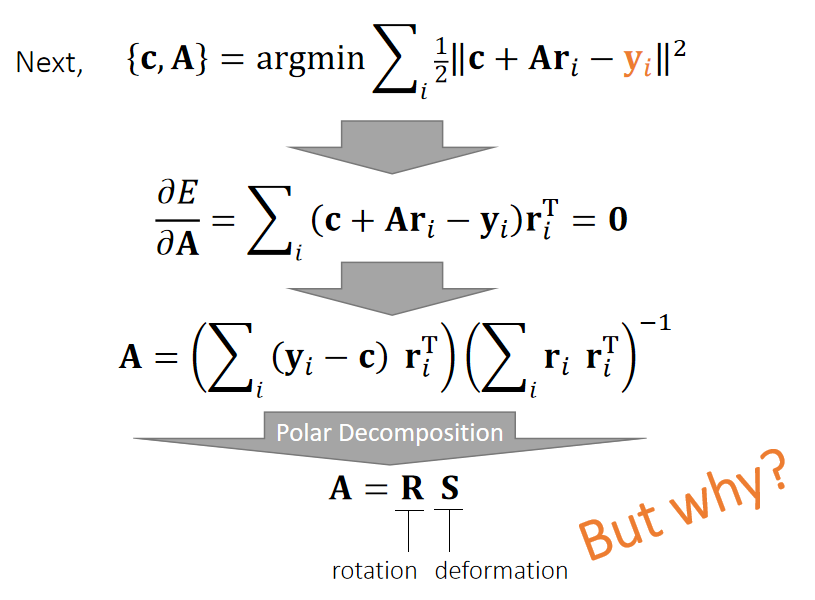
✅ 先假设 \(\mathbf{R}\) 是任意矩阵 \(\mathbf{A}\),再从中提取旋转成分
✅ Polar Decomposition：极性分解，把任意矩阵分解旋转部分和形变部分。

P36

极性分解

Singular value decomposition says any matrix can be decomposed into: rotation,scaling and rotation: \(\mathbf{A = UDV} ^T\).

We can rotate the object back before the final rotation: \(\mathbf{A} = (\mathbf{UV} ^T)(\mathbf{VDV} ^T)\).

✅ \(\mathbf{A} = （\mathbf{UV}^T）(\mathbf{VDV}^T) =\mathbf{RS}\)
\(\mathbf{R}\) 代表全局旋转，\(\mathbf{S}\)代表本地形变，扔掉S保留R。

$$ \mathbf{A=RS} $$

$$ \mathbf{A} ^T\mathbf{A} = \mathbf{S} ^T\mathbf{S} = \mathbf{S} ^2 $$

分解结果:unique

P39

Shape Matching Pipeline

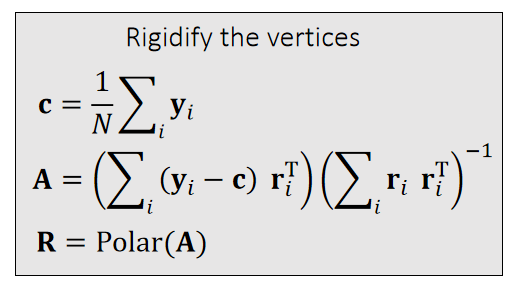
Physical quantities are attached to each vertex, not to the entire body.

P40

算法分析

  • 优点：Easy to implement and compatible with other nodal systems, i.e., cloth, soft bodies and even particle fluids.

  • 局限性：Difficult to strictly enforce friction and other goals. The rigidification process will destroy them.

  • 适用场景：More suitable when the friction accuracy is unimportant, i.e., buttons on clothes.

P41

After-Class Reading

Muller et al. 2005.
Meshless Deformations Based on Shape Matching. TOG (SIGGRAPH).

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/