补充1： Cross Product as a Matrix Product

We can convert the cross product $\mathbf{r}\times$ into a matrix product $\mathbf{r}^*$.

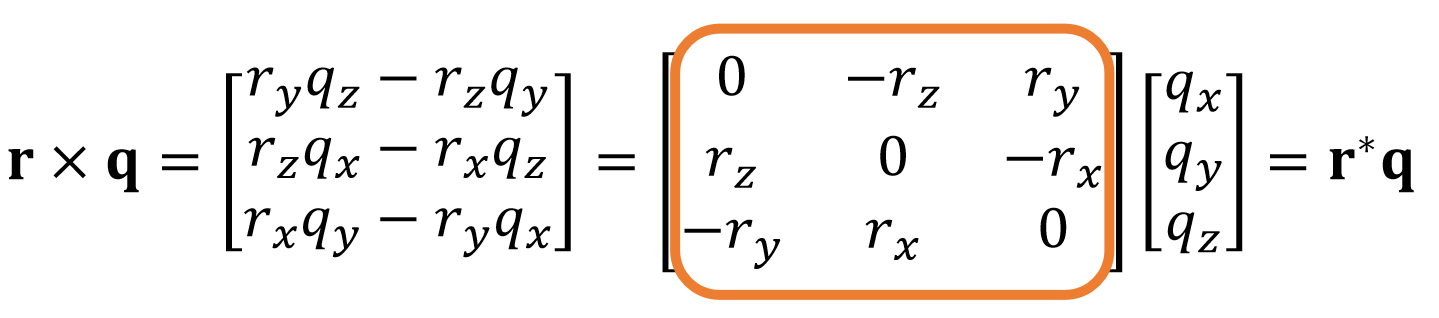
✅ $\mathbf{r}^*$ 是 $\mathbf{r}$ 的 cross matrix.
目的：用矩阵形式代替叉乘形式，方便公式化简

补充2：极性分解

Singular value decomposition says any matrix can be decomposed into: rotation,scaling and rotation: $\mathbf{A = UDV} ^T$.

We can rotate the object back before the final rotation: $\mathbf{A} = (\mathbf{UV} ^T)(\mathbf{VDV} ^T)$.

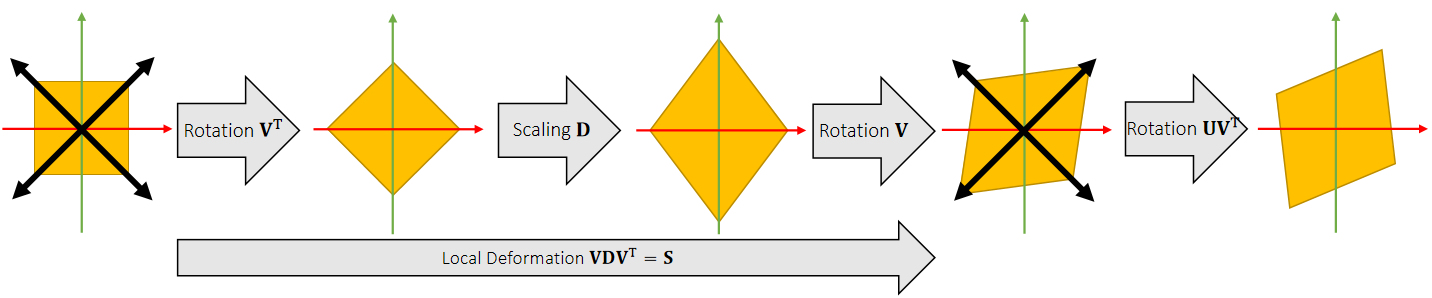
✅ $\mathbf{A} = （\mathbf{UV}^T）(\mathbf{VDV}^T) =\mathbf{RS}$
$\mathbf{R}$ 代表全局旋转，$\mathbf{S}$代表本地形变，扔掉S保留R。

$$ \mathbf{A=RS} $$

$$ \mathbf{A} ^T\mathbf{A} = \mathbf{S} ^T\mathbf{S} = \mathbf{S} ^2 $$

分解结果:unique

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/