时间步长

库朗-弗里德里希斯-列维条件是确定时间步长的一种常用方法。当前大多数仿真方法都根据CFL条件在每个时间步计算一个全局时间步长。通常，CFL条件的形式如下：

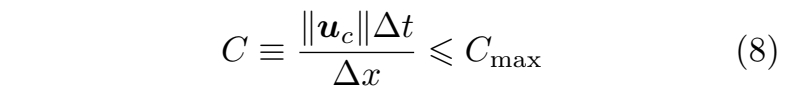
其中 \(‖u_c‖\) 表示信息传播速度，\(∆x\) 在欧拉或混合仿真中代表网格单元尺寸，在拉格朗日方法中则指光滑长度。\(C_{\mathrm{max} }\) 是一个基于离散算子大小的常数，\(C\) 即为CFL数或库朗数。在实际应用中，\(‖u_c‖\) 通常指材料中的声速或仿真中的最大流速。

时间步长 \(∆t\) 的选择通常使得 \(C\) 处于 [0, 1] 范围内。最大库朗数\(C_{\mathrm{max} }\)的选取一般取决于所用仿真算法的类型，但其值不应超过 1。相较于SPH方法，PIC或MPM等方法在选择 \(C_{\mathrm{max} }\)时通常具有更大的灵活性。在使用隐式时间积分方案时，可以在保持仿真稳定的前提下，采用更大的 \(C_{\mathrm{max} }\)值。