Two Types of Simulation Approaches

数值模拟方法可分为拉格朗日方法和欧拉方法两大类。

Lagrangian Approach	Eulerian Approach
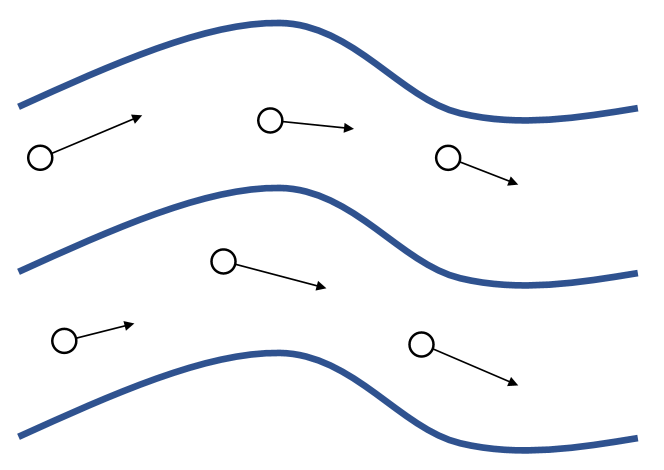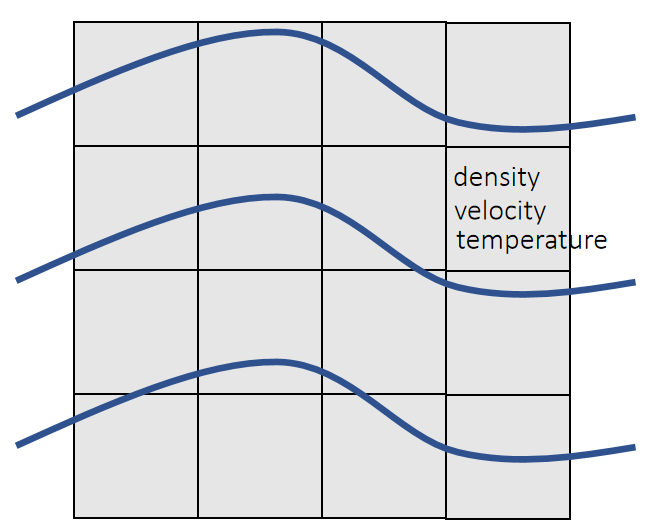✅ 无 Grid. 物理量附加在粒子上，粒子运动时更新自身物理量。	✅ 固定 Grid. 物理量固定在 Grid 上。粒子运动后统一新格子的物理量。
拉格朗日法中计算网格随物质一起变形，可方便地跟踪材料界面和引入与变形历史相关的材料模型，但对于涉及特大变形的问题会因网格严重畸变而产生数值求解困难，且难以有效地模拟材料的破碎、融化和汽化等行为。此类方法代表性程序为DYAN。	欧拉法中计算网格固定在空间中，不存网格畸变问题，但不易跟踪材料界面，且非线性对流项也会导致数值求解困难。

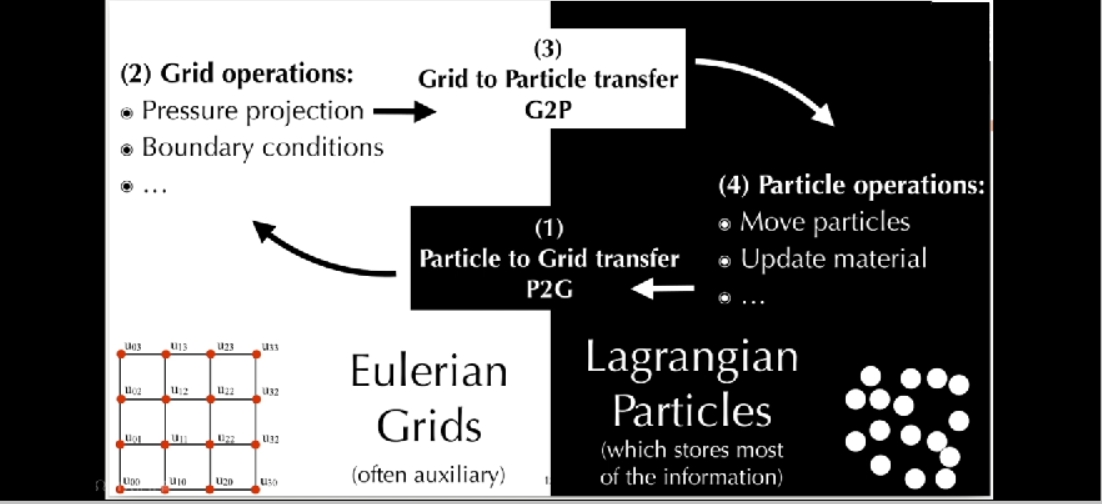
粒子法与网格法的结合

$$ \frac{D}{Dt} = \frac{\partial}{\partial t} + U \cdot \nabla $$

这个公式将欧拉法与拉格朗日法联系在一起 \(\frac{\partial}{\partial t}\) 代表固定点物理属性随时间的变化。
\(\frac{D}{Dt}\) 代表流动粒子的物理属性随时间的变化。
\(U \cdot \nabla\) 代表物理属性随位置的变化。

欧拉网格上的物理属性基于 \(\frac{\partial}{\partial t}\) 更新。 拉格朗日粒子上的物理属性基于 \(\frac{D}{Dt}\) 更新。

Motivation

• Recall that a fluid solver usually has two components:
  • Advection (evolving the fields)
  • Projection (enforcing incompressibility)
• Eulerian grids are really good at projection:
  • Easy to discretize
  • Efficient neighbor look-up
  • Easy to precondition (geometric multigrid)
• But Eulerian grids are bad at advection...
  • Dissipative: loss of energy and geometry

常见方法

补充：格子玻尔兹曼方法不是混合法

与上面讨论的 MPM / PIC / FLIP 容易混淆的是格子玻尔兹曼方法（LBM）。它同样以"格子 + 粒子"的形式出现在文献里，但两处"粒子"的含义完全不同：

• MPM / PIC / FLIP 的粒子是空间中的物质点，位置可以在空间中连续自由变化，跨时间步携带质量、速度、形变梯度等状态，并且会把信息映射回网格（P2G / G2P 双向耦合）。
• LBM 的"粒子"是速度空间的离散，只有预先规定的有限个方向（D2Q9 为 9 个方向，D3Q19 为 19 个方向）。它的位置被限制在格点上，没有空间自由度；格点上跨时间步保持的状态是实数分布函数 fᵢ，而不是粒子对象。

判定标准是：这次仿真里是否存在一个位置能够连续自由变化、且跨时间步保持状态、并与网格双向交换信息的点。

因此 LBM 归欧拉式一族，与网格法共享"状态挂在固定离散位置、只与局部邻域耦合、同步更新"的骨架。它相对常规模格法的差别在于状态变量与规则来源：状态是速度分布函数而非宏观量，规则来自玻尔兹曼方程的离散，而非 Navier-Stokes 方程的差分近似。详细讨论见 格子动理学方法。

发展趋势

1. 多尺度耦合：如量子-分子动力学-连续体的跨尺度模拟。
2. 机器学习加速：用神经网络替代部分网格求解或粒子交互。
3. 高性能计算优化：针对GPU/异构计算设计混合算法。

Reference

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/