P4

弹簧质点模型

✅ 整体流程就像是对 Mesh 上的每个顶点独立地进行粒子仿真，只是力变得复杂，因为在粒子之间增加了弹簧。当弹簧发生形变，就产生了弹簧力（内力）。
✅ 通过在粒子间构造弹簧来约束 Mesh 边长尽量不变。通过构造网状的弹簧系统来保证 Mesh 面片不发生形变。通过增加对角顶点的弹簧来约束 Mesh 体积上的形变。

---
title: 弹簧系统   
---
flowchart LR
    Current(["当前状态"]) 
    Constrain[("约束")]
    Outter[("外力")]
    Energy(["能量"]) 
    Force(["内力"]) 
    Next(["下一时刻状态"]) 

    Constrain-->Energy-->Force
    Outter & Force & Current --> Integrate --> Next --> Current

积分可以是显式积分或者隐式积分。如果是显式积分，由力得到速度，速度更新状态。

---
title: 弹簧系统 - 显式积分   
---
flowchart LR
    Current(["当前状态"]) 
    Constrain[("约束")]
    Outter[("外力")]
    Energy(["能量"]) 
    Force(["内力"]) 
    Velocity(["速度"]) 
    Next(["下一时刻状态"]) 

    Constrain-->Energy-->Force
    Outter & Force --> Velocity
    Velocity & Current --> Next

但显式积分存在不稳定性问题，在图形学中更常用的是隐式积分。

---
title: 弹簧系统 - 隐式积分   
---
flowchart LR
    Current(["当前状态"]) 
    Constrain[("约束")]
    Outter[("外力")]
    Energy(["势能能量"]) 
    Mometen(["动能能量"]) 
    Target(["优化目标"])
    Velocity(["速度"]) 
    Next(["下一时刻状态"]) 
    NextWoContrain(["不考虑约束的下一时刻状态"])

    Outter --> Velocity
    Velocity & Current --> NextWoContrain --> Mometen
    Constrain-->Energy 
    Energy & Mometen --> Target --> Optimize --> Next

✅ 本节课所讲的套路：分析力/能量 → 隐式积分 → 通过优化解积分 → 更新，对弹簧系统、有限元、弹性体等各种物理模拟同样适用。区别在于如何构造能量和解优化问题。

构建弹簧系统

An Ideal Spring —— 一个端点

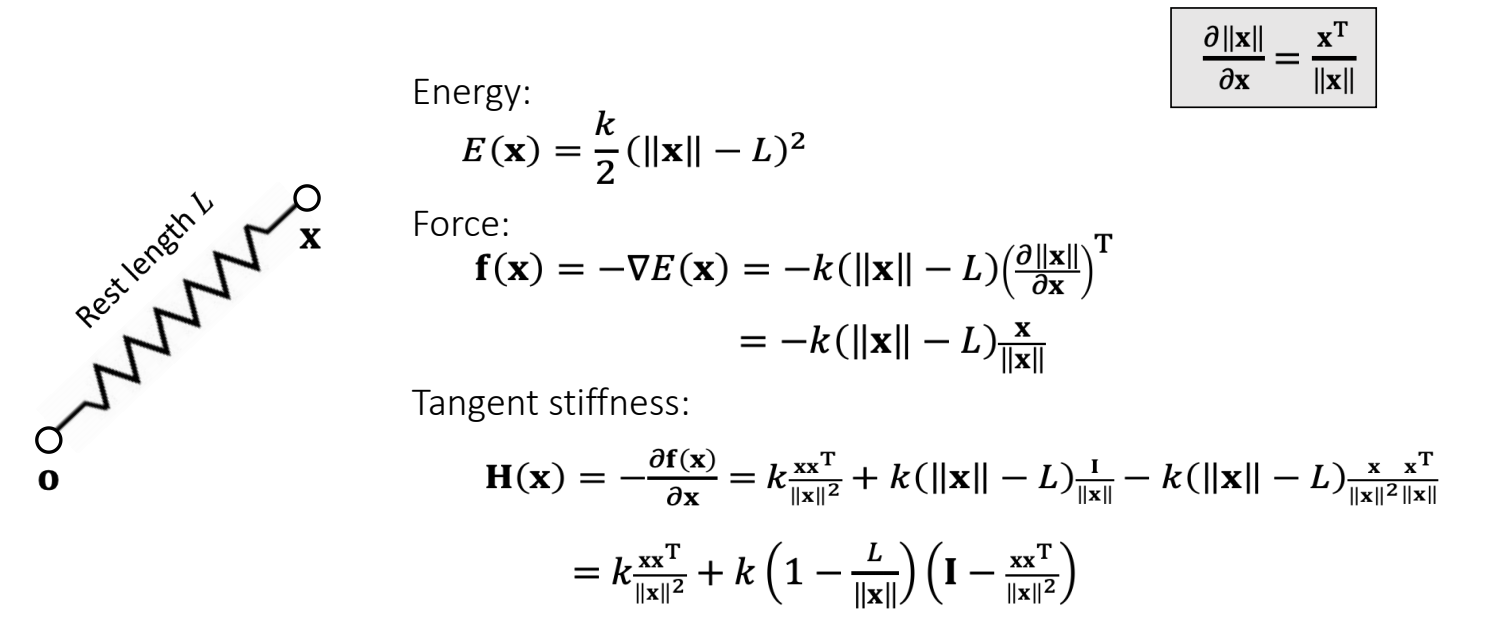
✅ Energy：物理上的弹性势能
✅ Force：物理上的力，是 Energy 的 gradient 的反方向; 公式后面有个 T,来源于前面的\(\nabla \)，直观解释，前面是力的大小，后面是力的方向。
🔍 Choi and Ko. 2002. Stable But Responive Cloth. TOG (SIGGRAPH) --- 以上公式推导的详细过程

An Ideal Spring —— 两个端点

$$

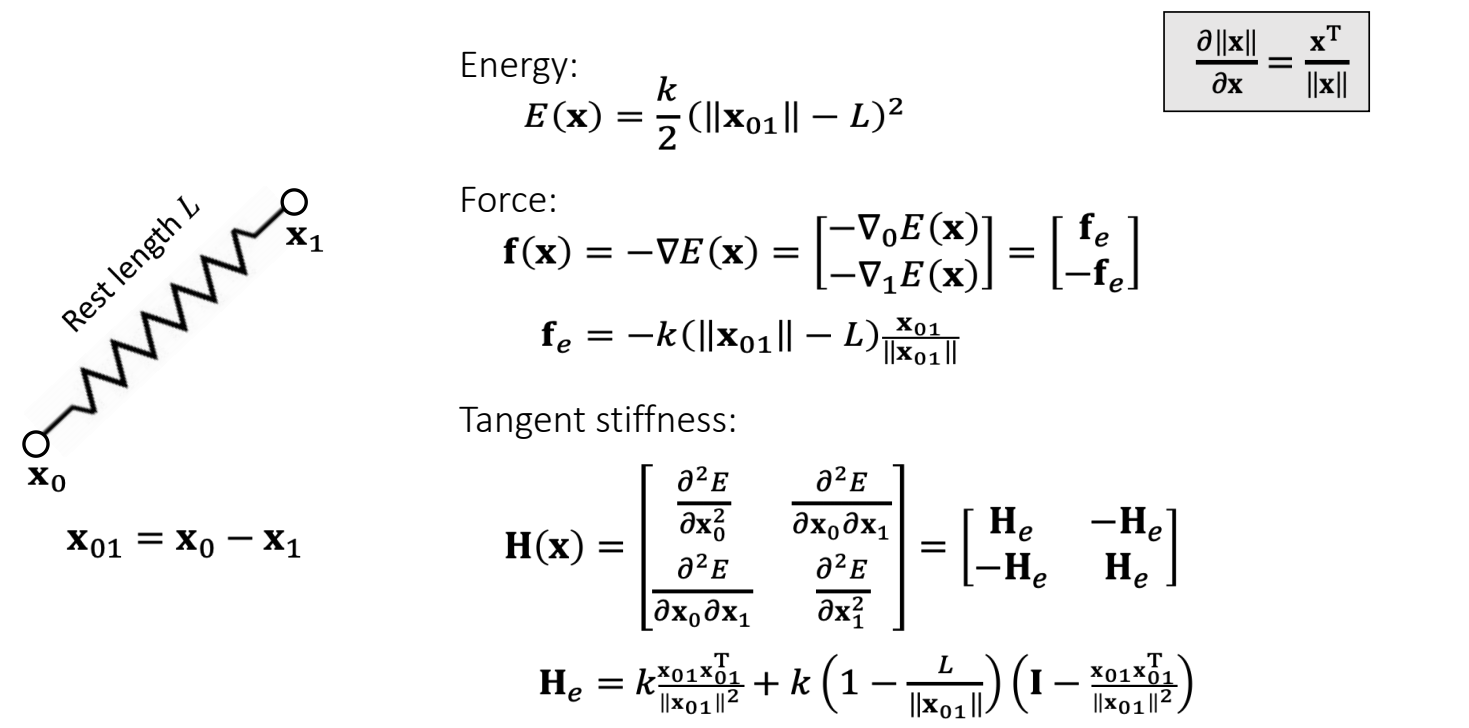
\mathbf{f} _i(\mathbf{x} )=−∇_i\mathbf{E} =−k(||\mathbf{x}_i −\mathbf{x}_j||−L)\frac{\mathbf{x}_i −\mathbf{x}_j}{||\mathbf{x}_i −\mathbf{x}_j ||} \\ \mathbf{f} _j(\mathbf{x})=−∇_jE=−k (||\mathbf{x}_j −\mathbf{x}_i ||−L)\frac {\mathbf{x}_j −\mathbf{x}_i}{||\mathbf{x}_j −\mathbf{x}_i||}

$$

P5

Multiple Springs

When there are many springs, the energies and the forces can be simply summed up.

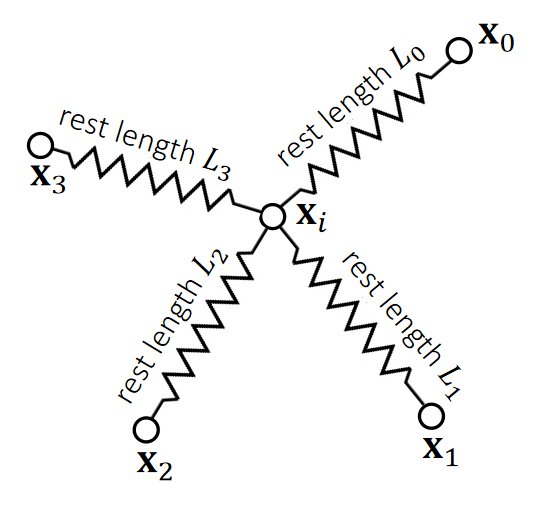
$$ E= {\textstyle \sum_{e=0}^{3}}E_e= {\textstyle \sum_{e=0}^{3}} (\frac{1}{2} k(||\mathbf{x} _i −\mathbf{x}_e ||−L_e)^2) $$

$$ f_i=−\nabla_iE = \textstyle \sum_{e=0}^{3}(−k(||\mathbf{x}_i−\mathbf{x}_e||−L_e)\frac{\mathbf{x}_i−\mathbf{x}_e}{||\mathbf{x}_i−\mathbf{x}_e||}) $$

✅ 能量和力都是可以叠加的

积分系统——显式积分

P12
与粒子仿真相同。每个 Mesh 顶点根据受力更新位置的过程涉及积分。积分离散化也可以是显式、隐式、半隐式。

Explicit integration suffers from numerical instability caused by overshooting, when the stiffness \(k\) and/or the time step \(∆t\) is too large.

✅ Explicit：当前力 → 当前速度 → 当前位置
显式积分不稳定，如果 \(Δt\) 或 \(k\) 太大，会导致 overshooting。

A naive solution is to use a small \(∆t\) . But that slows down the simulation.

✅ 解决方法：减小\(\Delta t\)。但这个方法不解决本质问题，且会降低整个模拟系统的效率
✅ 本质上是\(Δt\)太大导致积分近似的结果与实际积分的结果有很大误差，\(k\)太大或\(Δt\)只是让这个问题更明显，减小\(k\)或\(Δt\)问题仍然存在。

P13

积分系统——隐式积分

Implicit integration is a better solution to numerical instability. The idea is to integrate both x and v implicitly.

✅ Explicit和Implicit都是用某个时刻的力代表整个 \(Δt\) 时间的力，就都会出现上述误差。
✅ 区别在于，Explicit用当前力，往往使结果变大，产生爆炸，Implicit用未来力，往往使结果变小，产生消失。
✅ 消失只是结果不对。但爆炸会让结果崩溃，这是最不可接受的问题。因此用隐式代替显式。

隐式积分相对稳定，可以使用稍大的 \(Δt\)，但也存在以下问题：

1. 实现复杂，因此难以优化。
2. 每个 \(Δt\) 的求解更耗时，因此不一定会更快。
3. 可能出现数值振荡。

二元非线性方程组 -> 一元非线性方程

隐式积分用未来力计算未来速度，用未来速度计算未来位置。未来力，未来速度，未来位置都是未知量，不能直接求解，需要解方程。

✅ 粒子和刚体的仿真中使用了半隐式积分(现在的力，未来的速度)。

✅ 质点的质量可以不同吗？
答：可以不同。先根据三角形的面积计算三角的质量，再把质量分配到各个顶点上。
M是一个3n*3n的对角矩阵，具体形式为：
$$ M = \begin{pmatrix} m_1 I_3 & 0 & \cdots & 0 \ 0 & m_2 I_3 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & m_n I_3 \end{pmatrix} $$

假设F是一个保守力，即F是只与x有关的非线性函数，那么公式中的f[1]不是一个新的未知量。

✅ holonomic：力的大小和方向只跟位置有关，跟速度无关。例如重力，弹力。那么 \(f\)可以写成关于位置的函数\(f(x)\)。但\(f(x)\)不一定是线性的。

公式 2 代入公式 1 并消元，得：

$$ \mathbf{v} ^{[1]}=\mathbf{v}^{[0]}+∆t\mathbf{M} ^{−1}\mathbf{f} (\mathbf{x}^{[0]}+∆t\mathbf{v} ^{[1]}) $$

或把公式1代入公式2并消元，得：

消元得：
$$ \mathbf{x} ^{[1]}=\mathbf{x} ^{[0]}+\Delta t\mathbf{v} ^{[0]}+\Delta t^2\mathbf{M} ^{-1}\mathbf{f}(x^{[1]}) $$

对x或v消元，解法都是类似的。最后都转化为解非线性方程的问题。

线性近似法：求解一元非线性方程->解线性系统

✅ 近似成线性问题后直接解方程。这种方法相当于每一个Step做了一次牛顿法。

以对x消元结果为例，\(\mathbf{f}\) 在 \(\mathbf{x}^{[0]}\) 处泰勒展开，得：

$$ \mathbf{v} _{t+1}=\mathbf{v}_t+∆t\mathbf{M} ^{−1}[\mathbf{f} (\mathbf{x}_t)+\frac{\partial \mathbf{f} }{\partial \mathbf{x} }(\mathbf{x} _t) ∆t\mathbf{v} _{t+1}] $$

整理后得:

$$ [\mathbf{I}-∆t^2\mathbf{M} ^{−1}\frac{\partial \mathbf{f} }{\partial \mathbf{x} }(\mathbf{x} _t) ]\mathbf{v} _{t+1}=\mathbf{v}_t+∆t\mathbf{M} ^{−1}\mathbf{f} (\mathbf{x}_t) $$

这就成了一个解线性系统的问题。解线性系统见Linear Solver

问：为什么不直接求逆？
答：求逆太贵

这个公式再泛化一下，引入一个beta，就可以把隐式积分与之前的显式积分、中点法积分统一起来。

$$ [\mathbf{I} -\beta \Delta t^2\mathbf{M} ^{-1}\frac{\partial \mathbf{f} }{\partial \mathbf{x} }(\mathbf{x} _t )]\mathbf{v} _{t+1}=\mathbf{v} _t+\Delta t\mathbf{M} ^{-1}\mathbf{f} (\mathbf{x} _t) $$

❶ \(\beta\) = 0: forward/semi-implicit Euler (explicit)
❷ \(\beta\) = 1/2: middle-point (implicit)
❸ \(\beta\) = 1: backward Euler (implicit)

方法二：求解一元非线性方程->优化问题

构造优化目标F(x)：

$$ F(\mathbf{x}) = \frac{1}{2∆t^2}||\mathbf{x} −\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]}||_\mathbf{M}^2+E(\mathbf{x} ) $$

有： $$ \mathbf{x} ^{[1]} = \argmin F(\mathbf{x}) $$

✅ 前面方程解\({x} ^{[1]}\)等价于F(x)函数极小点。等价转换的推导在补充1。非线性方程问题为转化为优化问题。
✅ 其中：\(\mathbf{M}\)对角矩阵，描述质量，\(3N \times 3N\)。\(\mathbf{x}\)为 \(3N\times 1\)矢量,描述顶点信息。\(E\) 为所有的力的能量。\(\mathbf{||x||_M^2=x^TMx} \)。
✅ 只有保守力能用能量描述、非保守力（例如摩擦力）则不行。

定义 \(\mathbf{g(x)} =\mathbf{x} ^{[0]}+\Delta t\mathbf{v}^{[0]}+\Delta t^2M^{-1}f(\mathbf{x}^{[1]})-\mathbf{x} ^{[1]}\)
也可以得出：\(x^{[1]}=\mathrm{argmin} (g(\mathbf{x} )^2)\) 或 \(\mathbf{x}^{[1]}=\mathrm{argmin} |\mathbf{g(x)}|\)

只是这样构造出的优化问题，求导比较难计算。

P18

Newton’s Method：解优化问题->解线性系统

🔎 Newton-Raphson Method见补充2. 这里直接开始Newton方向在本当前场景的应用。

Specifically to simulation, we have:

$$ F (\mathbf{x} )=\frac{1}{2∆t^2} ||\mathbf{x} −\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]}||_\mathbf{M} ^2+\mathbf{E} (\mathbf{x} ) $$

$$ ∇F(\mathbf{x}^{(k)})=\frac{1}{∆t^2}\mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})−\mathbf{f}(\mathbf{x}^{(k)})=b $$ b $$ \frac{∂^2F (\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} =\frac{1}{∆t^2} \mathbf{M} +\mathbf{H} (x^{(k)})=\mathbf{A} $$

解线性系统 \(\Delta \mathbf{x} =b\)

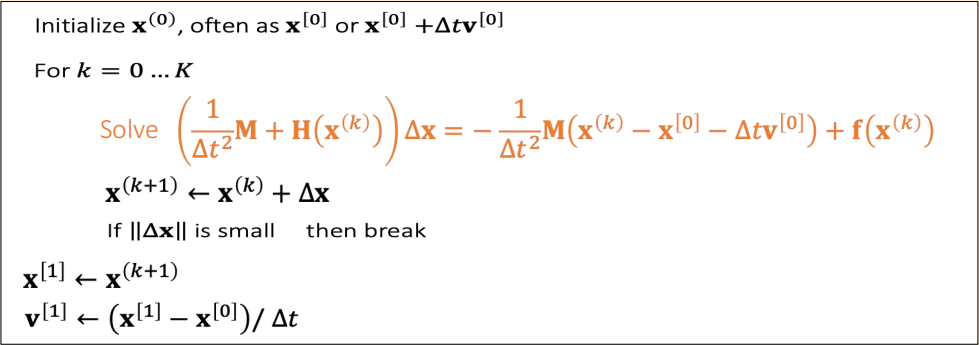
Positive Definiteness of Hessian

为了让优化问题收敛，我们希望A是正定的，具体原因见补充材料。

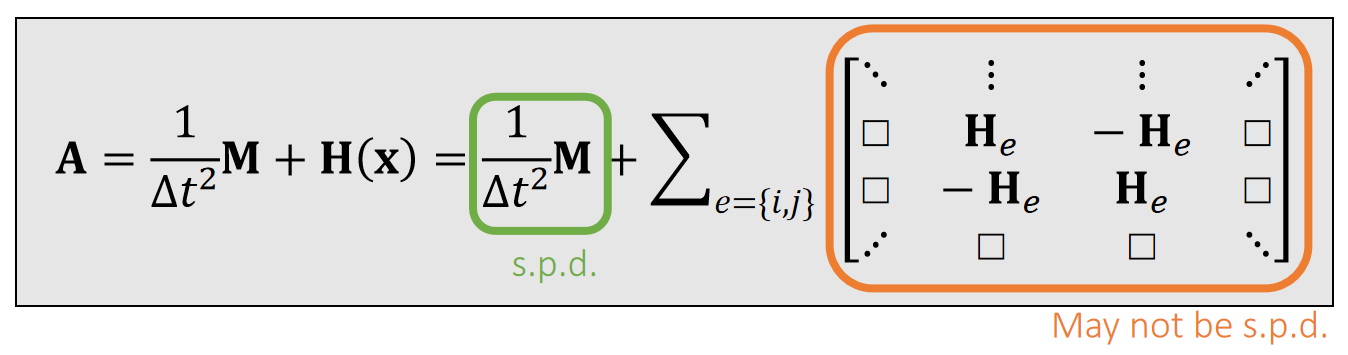
✅ 而A的正定性取决于\(H(x)\) 的正定性。 ✅ \(H(x)\)的维度是\(3N \times 3N\)，N 是弹簧数。每个\(H_e\)的维度是\(3 \times 3\)。它是由所有弹簧的H构成的。

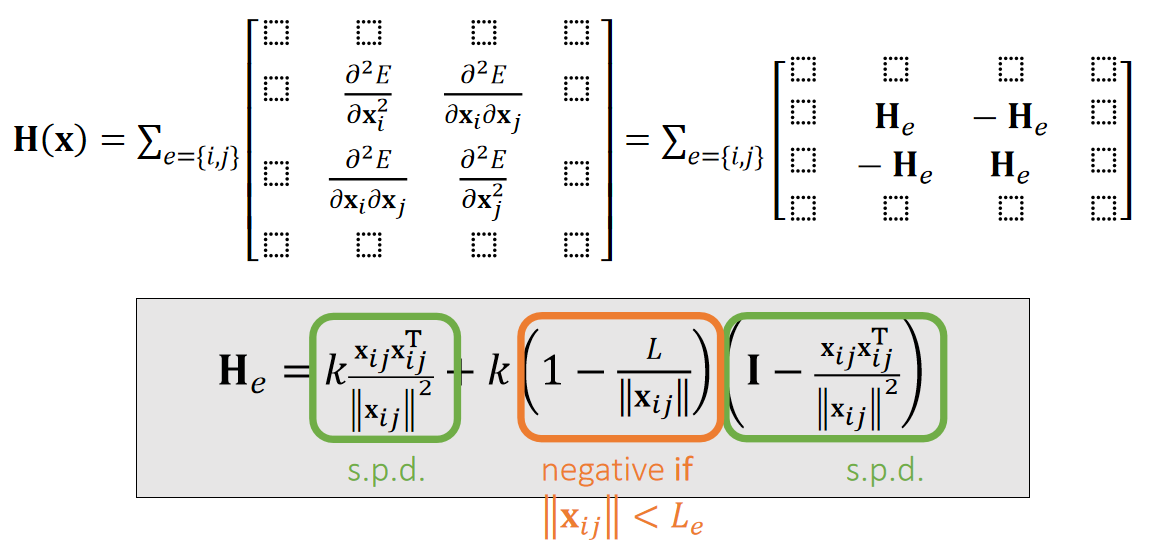
✅ H(x)的正定性则是由 \(H_e\) 的正定性决定。

下面分析\(H_e\)的正定性：
For any \(\mathbf{x} _{ij}, \mathbf{v} ≠0\),

$$ \mathbf{V}^\mathbf{T}\frac{{\mathbf{x} _{ij}\mathbf{x} _{ij}}^\mathbf{T} }{||\mathbf{x} _{ij}||^2}\mathbf{V}=||\frac{{\mathbf{x} _{ij}}^\mathbf{T} \mathbf{v} }{||\mathbf{x} _{ij}||}||^2> 0 $$

$$ \mathbf{V} ^\mathbf{T} (\mathbf{I} -\frac{{\mathbf{x} _{ij}\mathbf{x} _{ij}}^\mathbf{T} }{||\mathbf{x} _{ij}||^2}) \mathbf{V} =\frac{||\mathbf{x} _{ij}||^2||\mathbf{v} ||^2-||{\mathbf{x} _{ij}}^\mathbf{T} \mathbf{v} ||^2}{||\mathbf{x} _{ij}||^2}\ge 0 $$

✅ \( \mathbf{x}_ {ij}\) 代表顶点\( \mathbf{x}_ {i}\)和顶点\( \mathbf{x}_ {j}\)的位置的差。
✅ 最后一个公式分子满足柯西不等式
✅ 结论：\(||x_{ij}||< Le\). 代表弹簧处于压缩状态。此时 He 有可能非正定(可能有多个极小值点)，但拉伸时一定正定。
✅ He 正定则\(H(x)\)半正定，此时弹簧系统有唯一解。
✅ \(\Delta t\)越小，A越容易正定、弹簧系统越稳定。
✅ 但是A不正定，不代表没有唯一解。

P23

Enforcement of Positive Definiteness

✅ 不正定最大的问题不是解不唯一，因为解出任意一个解都能让模拟系统进行下去。
✅ 非正定的主要问题，是数学计算上的不稳定，可能导致解不出来；

• One solution is to simply drop the ending term, when \({\color{Orange}{ ||\mathbf{x} _{ij}||<\mathbf{L} _e}}:\)

✅ 简单粗爆的解决方法就是把后面这项删掉。

🔎 Choi and Ko. 2002. Stable But Responive Cloth. TOG (SIGGRAPH) --- 其它让He正定的方法

P27

After-Class Reading

🔎 Baraff and Witkin. 1998. Large Step in Cloth Simulation. SIGGRAPH.

✅这篇论文是衣服模拟的经典论文，第一个用隐式积分做衣服模型的论文。论文没有用弹簧系统，而是另一套模型。
✅ 关注其中解隐式积分的部分，没有做非线性优化或解非线性方程，而是把非线性方程线性化，等价于做一次牛顿迭代。
🔎 Fast mass - spring system solver

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/