FEM

Lecture 3 [31:48]

把空间分成极小的 element，例如三角形，四面体。

Linear Finite Element Method

The Linear FEM Assumption

✅ 假设：三角形的形变是均匀的

In a nutshell, linear FEM assumes that for any point $\mathbf{X}$ in the reference triangle, its deformed correspondence is: $\mathbf{x=FX+c}$.

✅ reference triangle：三角形处于没有发生形变的静止的状态。
✅ $\mathbf{X}$和$\mathbf{x}$可以分别是 reference 和 deformed 三角形的顶点或内部点，公式都同样适用。

一个向量对另一个向量求导，得到的是 Jacobian 矩阵。由于是均匀形变，在一个三角形内部，$\mathbf{F}$ 是一致的。

For any vector between two points, we can use F to convert it from reference to deformed:
$$ \mathbf{x} _{ba}=\mathbf{x} _b−\mathbf{x} _a=\mathbf{FX} _b+\mathbf{c} −\mathbf{FX} _a−\mathbf{c} =\mathbf{FX} _{ba}. $$

$J=\mathrm{det} (\mathbf{F} )$ 表示形变后的面积变化
弹性势能：
$$ \mathbf{U} (e)= \int _ e \psi (\mathbf{F} (x))dx=\mathbf{V} _e\psi (\mathbf{F} _e) $$

$\psi$ 是能量密度函数

如果采用显示积分，接下来根据能量计算力，再仿真。如果采用隐示积分，接下来基于能量做优化。
弹性势能量密度函数关于体积的积分，对于一个元素来说，$\mathbf{F}$ 是常数，$\psi (\mathbf{F})$ 也是常用数。

计算Deformation Gradient

Therefore, we can calculate the deformation gradient by edge vectors.

公式第二项只与 reference 有关，可以预计算。

Problem: $\mathbf{F}$ is related to deformation, but it contains rotation.

✅ 期望$\mathbf{F}$只包含形变量、不包含平移和旋转、因为刚体运动不应该有形变，所以要把形变提取出来。
✅平移已经在$\mathbf{c}$里面了，所以只需考虑旋转。

基于显式时间积分的 FEM

$$ \text{deformed mesh} \rightarrow \overset{形变}F {\rightarrow} \overset{能量密度}ψ{\rightarrow}\overset{能量}U{\rightarrow}力\rightarrow速度\rightarrow位置
$$

基于隐式时间积分的FEM.
与弹簧系统类似，但计算过程非常复杂。

从F中去除旋转

回顾SVD分解

Ideally, we need a tensor to describe shape deformation only. Recall that SVD gives $\mathbf{F=UDV^T}$, where only $\mathbf{V^T}$ and $\mathbf{D}$ are relevant to deformation.

✅ $\mathbf{V^T}$ 看上去是旋转、实际上是为了确定形变的方向、 $\mathbf{U}$ 才是真正的旋转
✅ 目的：把$\mathbf{F}$中的$\mathbf{U}$去掉、可以先做 $\mathbf{SVD}$ 分解再把$\mathbf{U}$去掉。但本文使用了更简单的方法

Green Strain

So we get rid of $\mathbf{U}$ as: $\mathbf{G} =\frac{1}{2} (\mathbf{F^TF−I} )=\frac{1}{2} (\mathbf{VD} ^2\mathbf{V} ^\mathbf{T} −\mathbf{I} )=\begin{bmatrix} \varepsilon _{uu} & \varepsilon _{uv}\\ \varepsilon _{uv} & \varepsilon _{vv} \end{bmatrix}$, Green strain.

✅ $\mathbf{G}$ 是一个描述物体形变的有无和大小矩阵，且与关旋转

If no deformation, $\mathbf{G=0}$; if deformation increases, ||$\mathbf{G}$|| increases.
Three deformation modes: $\varepsilon _{uu}$, $\varepsilon _{vv}$ and $\varepsilon _{uv}$.
$\mathbf{G}$ is rotation invariant: if additional rotation $\mathbf{R}$, then deformation gradient is $\mathbf{RF}$ but green strain is the same: $\mathbf{G} =\frac{1}{2} (\mathbf{F^TR^TRF−I} )=\frac{1}{2} (\mathbf{VD} ^2\mathbf{V} ^\mathbf{T} −\mathbf{I} )$.

弹性体的弹性势能

前面提到的能量公式是一种通用的形式。这里的能量计算过程是一种具体的广泛使用的公式。

Let $\mathbf{G}$ be the the green strain describing deformation. We consider the energy density per reference area as: $W (\mathbf{G})$.

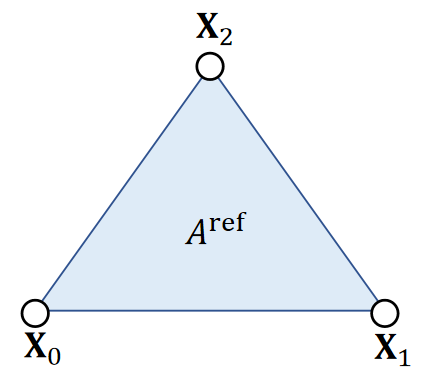
✅用形变程度来定义能量。$W$代表单位面积上的能量，因此称为能量密度。总能量为单位能量$\mathbf{X}$面积.
✅ $A^{ref}$ 为 reference status 下三角形的面积
✅ StVK是一种经典的能量密度函数（Strain Energy Density Function），在力学中不常用，但在图形学中很常用、原因是简单

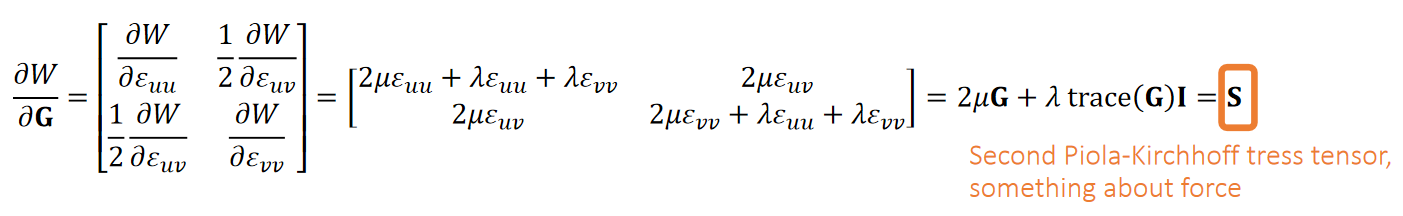
✅ S 是一个与力有关的物理量。会在FVM内容中进一步解释。
✅ 能量对位移求导是力。形变是一种位移。能量密度对位移求导是一种类似于力的密度的量。

计算Forces

Given everything we have, we can now calculate the forces.

✅ 力是形变施加到顶点上的力

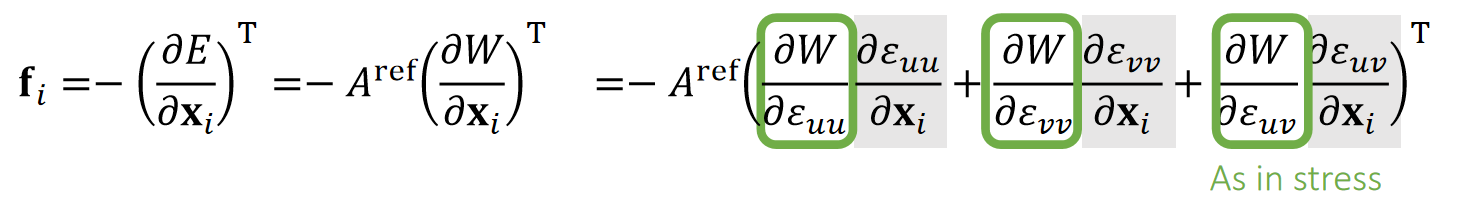
✅ 绿色部分是上一页S中的内容、灰色部分将在下一页推导。

方法一

Recall that,

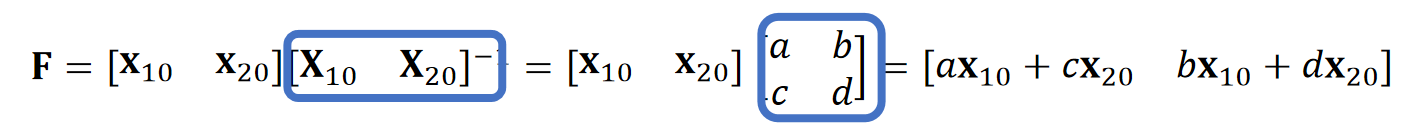
❗ $\mathbf{F}$不是力，是deformation gradient．
✅ 假设a,b,c,d是形变后的顶点。

By definition,
$$ \mathbf{G} =\frac{1}{2} (\mathbf{F^TF−I} )=\begin{bmatrix} \frac{1}{2}(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} (a\mathbf{x} _{10}+c\mathbf{x} _{20})−\frac{1}{2} & \frac{1}{2}(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} (b\mathbf{x} _{10}+d\mathbf{x} _{20})\\ \frac{1}{2}(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} (b\mathbf{x} _{10}+d\mathbf{x} _{20}) & \frac{1}{2}(b\mathbf{x} _{10}+d\mathbf{x} _{20})^\mathbf{T} (b\mathbf{x} _{10}+d\mathbf{x} _{20})−\frac{1}{2} \end{bmatrix} $$

So:

$$ \frac{∂\varepsilon _{uu}}{∂\mathbf{x} _1}=a(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} \quad\quad \frac{∂\varepsilon _{vv}}{∂\mathbf{x} _1}=b(b\mathbf{x} _{10}+d\mathbf{x} _{20})^\mathbf{T} \quad\quad \frac{∂\varepsilon _{uv}}{∂\mathbf{x} _1}=\frac{1}{2} a(b\mathbf{x} _{10}+d\mathbf{x} _{20})^\mathbf{T} +\frac{1}{2} b(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} $$

$$ \frac{∂\varepsilon _{uu}}{∂\mathbf{x} _2}=c(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} \quad\quad \frac{∂\varepsilon _{vv}}{∂\mathbf{x} _2}=d(b\mathbf{x} _{10}+d\mathbf{x} _{20})^\mathbf{T} \quad\quad \frac{∂\varepsilon _{uv}}{∂\mathbf{x} _2}=\frac{1}{2} c(b\mathbf{x} _{10}+d\mathbf{x} _{20})^\mathbf{T} +\frac{1}{2} d(a\mathbf{x} _{10}+c\mathbf{x} _{20})^\mathbf{T} $$

✅ $\mathbf{x}$为current边的矩阵，$\mathbf{r}$为reference边的矩阵。

P10

方法二

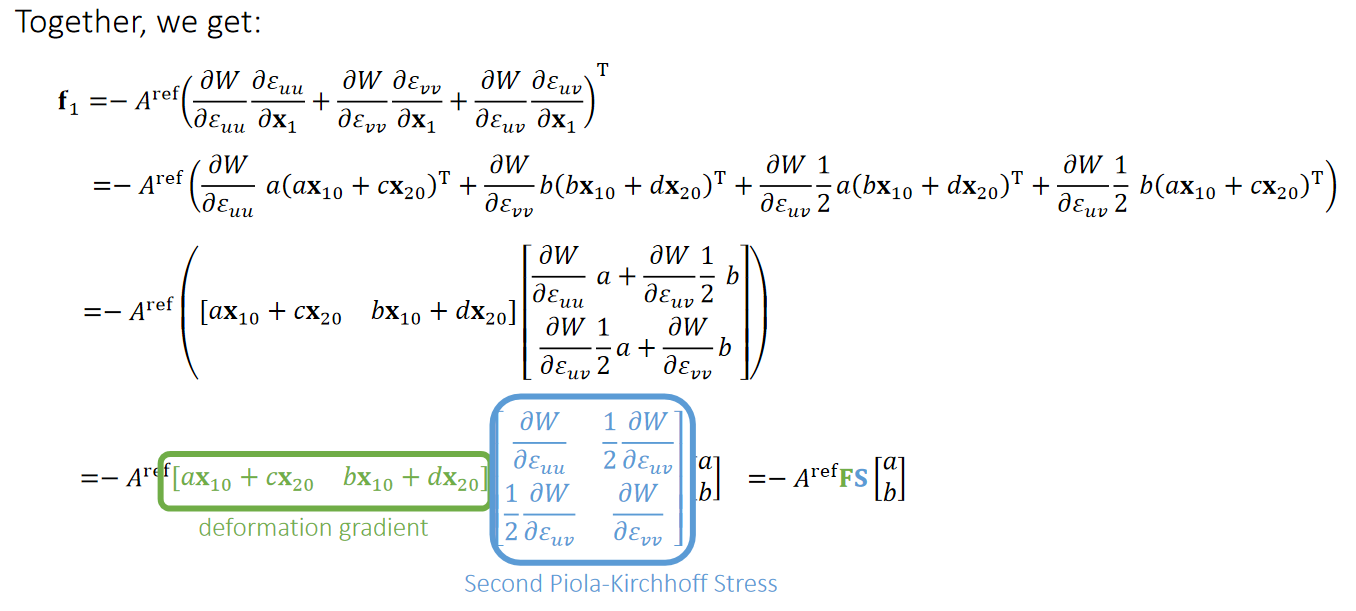
✅ 把 P9 代入 P8 得到 P10
✅ 上一页推导方法从定义出来，过程简单，但很容易出错。这里用矩阵来简化计算，得到同样的结果。

P11

结论

In conclusion, we have:

$$ \mathbf{f} _1=−A^{\mathrm{ref} }\mathbf{FS} \begin{bmatrix} a\\ b \end{bmatrix} \quad\quad \mathbf{f} _2=−A^{\mathrm{ref} }\mathbf{FS} \begin{bmatrix} c\\ d \end{bmatrix} $$

$$ \begin{bmatrix} \mathbf{f} _1 &\mathbf{f} _2 \end{bmatrix}= − A ^{\mathrm{ref} }\mathbf{FS} \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} \end{bmatrix}^\mathbf{−T} $$

✅ $f_0=-f_1-f_2$

P12

Implementations

🔎 Volino et al. 2009. A simple approach to nonlinear tensile stiffness for accurate cloth simulation. TOG

Only talks about cloth (2D reference -> 3D deformation)

What about tetrahedron (3D reference -> 3D deformation)?
- Same idea, but everything is now in 3D.
- Deformation gradient $\mathbf{F} \in \mathbf{R} ^{3×3}$
- Green strain $\mathbf{G} \in \mathbf{R} ^{3×3}$
- Stress tensor $\mathbf{S} \in \mathbf{R} ^{3×3}$
- Forces $\mathbf{F}_i \in \mathbf{R} ^3$

FEM 不擅长处理自碰撞。

隐式积分

Recall backward Euler time integration:

$$ [\mathbf{I} -\Delta t^2\mathbf{M} ^{-1}\frac{\partial \mathbf{f} }{\partial \mathbf{x} }(\mathbf{x} _t)]\mathbf{v} _{t+1}=\mathbf{v} _t+\Delta t\mathbf{M} ^{-1}\mathbf{f} (\mathbf{x} _t) $$

Want implicit time integration? Compute force differentials $\frac{\partial \mathbf{f} }{\partial \mathbf{x} } =\frac{\partial^2\Psi }{\partial \mathbf{F} ^2} $

Question: in both explicit and implicit schemes, how to compute $m_i$? Use mass lumping (or any other convenient approximation you want...)

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/