P29

The Bending Spring Issue

A bending spring offers little resistance when cloth is nearly planar, since its length barely changes.

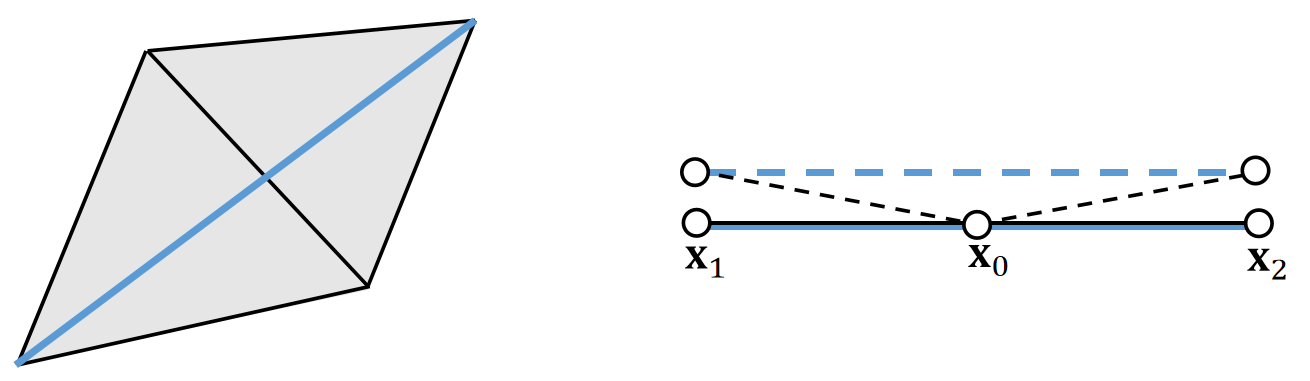
✅黑线为三角形面片，每条边一根弹簧，并增加一根蓝线弹簧，构成弯曲弹簧，阻止两个面片弯折。
存在的问题：小的弯折，弹簧长度几乎不变，抵抗弯曲的力量非常弱。（不适用于类似于纸的弯折效果）。

P30

A Dihedral Angle Model

A dihedral angle model defines bending forces as a function of \(\theta : \mathbf{f} _i=f (\theta )\mathbf{u} _i\).

✅ Dihedarl Angel:二面角
✅ 把弯曲的力写成关于二面角的函数

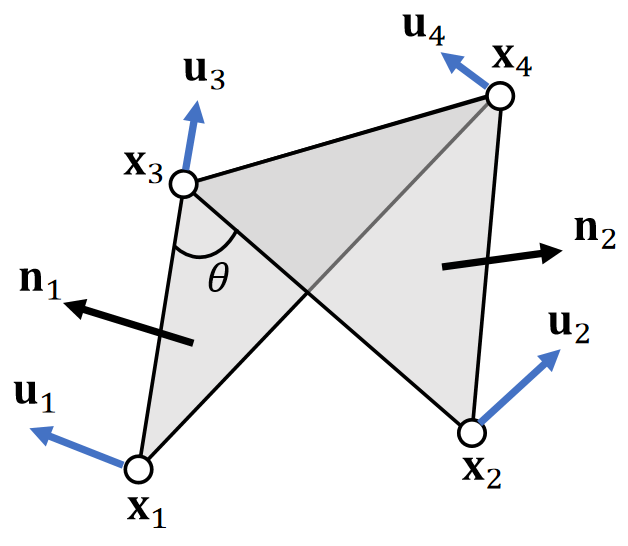
✅ \(x_1, x_2, x_3, x_4\) 都会受到 bending force. 力的大小相同但方向不同，但都是关于二面角的函数。
✅\(u_i\)：描述力的方向，与\(\theta\)大小无关。\(f(\theta)\)：描述力的大小，是关于\(\theta\)的函数。

• First, \(\mathbf{u}_1\) and \(\mathbf{u}_2\) should be in the normal directions \(\mathbf{n}_1\) and \(\mathbf{n}_2\).

• Second, bending doesn’t stretch the edge, so \(\mathbf{u}_4\)−\(\mathbf{u}_3\) should be orthogonal to the edge, i.e., in the span of \(\mathbf{n}_1\) and \(\mathbf{n}_2\).

• Finally, \(\mathbf{u}_1+\mathbf{u}_2+\mathbf{u}_3+\mathbf{u}_4=\mathbf{0}\), which means \(\mathbf{u}_3\) and \(\mathbf{u}_4\) are in the span of \(\mathbf{n}_1\) and \(\mathbf{n}_2\).

✅ 合力为0。

P31
Conclusion:

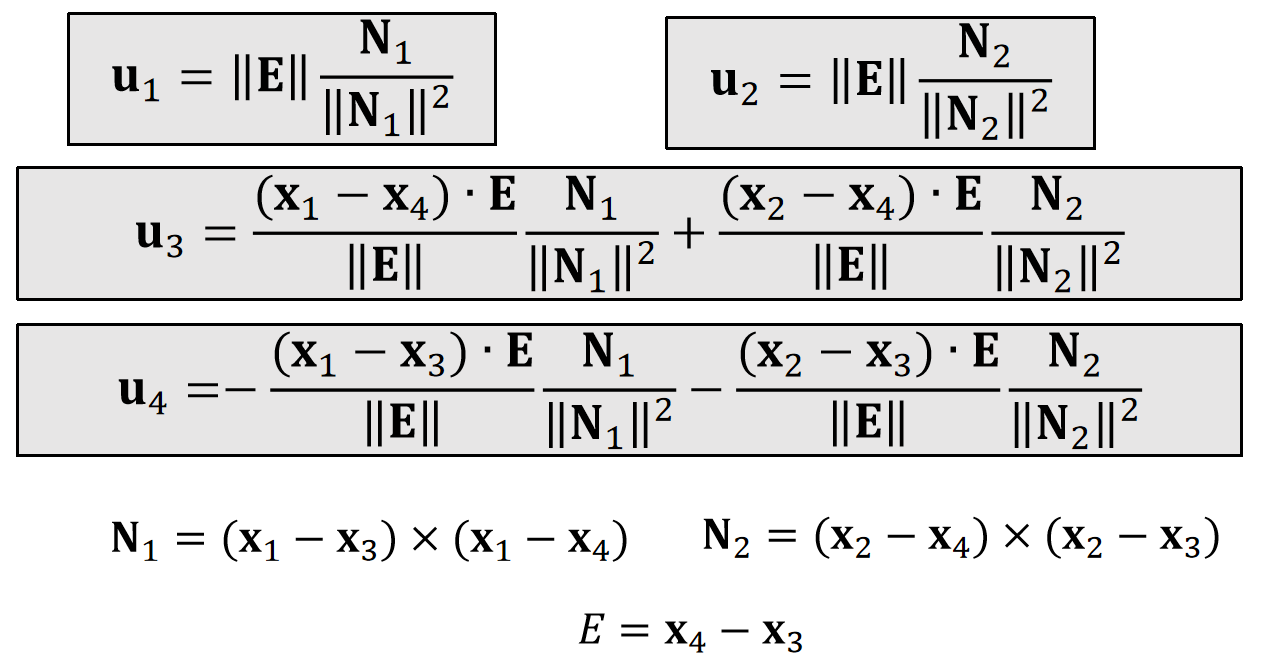
✅ N是未归一化的 normal. N 的方向与 normal 相同。大小为三角形的面积。
✅ 重要的不是结果，而是根据观察进行合理假设的思考过程。

P32

Planar case:

$$ \mathbf{f} _i=k\frac{||\mathbf{E}||^2}{||\mathbf{N}_1||+||\mathbf{N}_2||} \sin(\frac{π−\theta}{2})\mathbf{u} _i $$

Non-planar case:

$$ \mathbf{f} _i=k\frac{||\mathbf{E} ||^2}{||\mathbf{N} _1||+||\mathbf{N} _2||}(\sin(\frac{π−\theta}{2})-\sin(\frac{π−\theta_0}{2}))\mathbf{u}_i $$

✅ Non-planar case：不是指弯曲时的力，而是指静止状态(reference state)为非平面的场景下，弯曲为\(\theta\)时的力。\(\theta_0\)表示 reference state. ✅ 老师没解释公式怎么来的
🔎 Bridson et al. 2003. Simulation of Clothing with Folds and Wrinkles. SCA.
✅ 此论文适合读完。除了弯曲模型，还有一些有意思的设计。

Explicit integration.
Derivative is difficult to compute.

✅ 由于完全基于力而不考虑能量，适合用显式积分。

P34

A Quadratic Bending Model

✅二面角方法是纯分析力的方法，比较复杂。此处是Bending issue的另一个方法。

A quadratic bending model has two assumptions: 1) planar case; 2) little stretching.

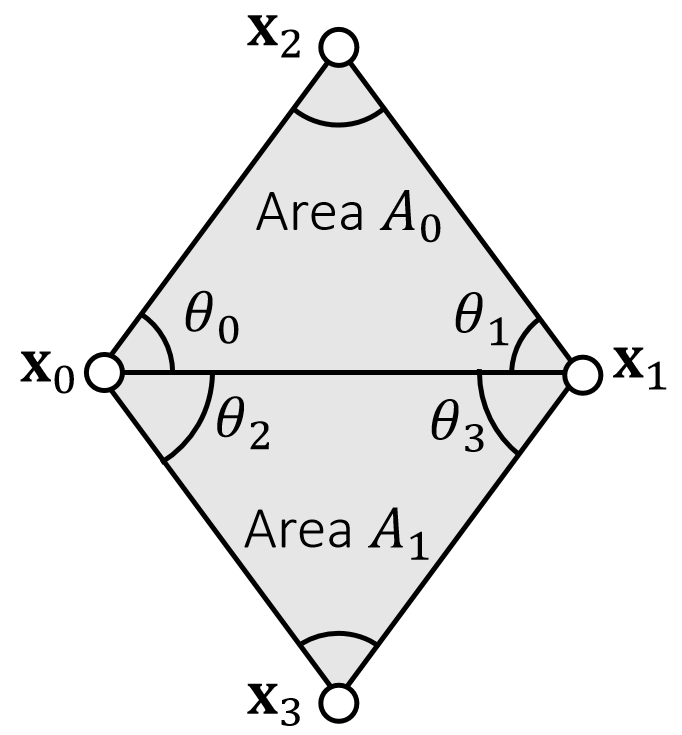
$$ E(\mathbf{x} )=\frac{1}{2} \begin{bmatrix} \mathbf{x}_0 & \mathbf{x}_1 & \mathbf{x}_2 & \mathbf{x}_3 \end{bmatrix}\mathbf{Q} \begin{bmatrix} \mathbf{x}_0 \\ \mathbf{x}_1 \\ \mathbf{x}_2\\ \mathbf{x}_3 \end{bmatrix} $$

$$ \mathbf{Q} =\frac{3}{\mathbf{A} _0+\mathbf{A} _1}\mathbf{qq^T} $$

✅ \({\mathbf{A} _0}\)和\({\mathbf{A} _1}\)是两个三角形在reference状态下的面积。

$$ \mathbf{q} = \begin{bmatrix} (\cot\theta _1+ \cot\theta _3)\mathbf{I} \\ (\cot\theta _0+ \cot\theta _2)\mathbf{I} \\ (-\cot\theta _0- \cot\theta _1)\mathbf{I} \\ (-\cot\theta _2- \cot\theta _3)\mathbf{I} \end{bmatrix} $$

\(\mathbf{I}\) is 3-by-3 identity.

✅ \(\mathbf{Q}\)只与\(\mathbf{\theta}\)有关，因此是一个定值。

It’s not hard to see that: \(E (\mathbf{x} )=\frac{3||\mathbf{q} ^\mathbf{T}\mathbf{x} ||^2}{2(A_0+A_1)}\). Also, \(E (\mathbf{x} )=0\) when the triangles are flat.

✅ \(\mathbf{q^T}\mathbf{x}\)在估算两个三角形的拉普拉斯，即两个三角的曲率、当两个三角形共面时， \(E(\mathbf{x})=0\)
🔎 离散曲面的拉普拉斯，见GAMES102
✅ \(E(\mathbf{x})\) 来自数学上曲率的推导，而不是来自物理意义的推导。
✅ 问题：能量的思想能用在刚体上吗？
答：这里的能量是弹性能量、刚体无弹性，因此也无所谓能量。

Pros of The Quadratic Bending Model

• Easy to implement:

✅ \(E(\mathbf{x})\)是关于\(\mathbf{x}\)的二次函数，很容易计算\(E(\mathbf{x})\)的一阶导（力）和二阶导\(\mathbf{H} \)

$$ \mathbf{f} (\mathbf{x} )=−\nabla \mathbf{E} (x)= −\mathbf{Q} \begin{bmatrix} \mathbf{x} _0\\ \mathbf{x} _1\\ \mathbf{x} _2 \\ \mathbf{x} _3 \end{bmatrix} $$

$$ \mathbf{H} (\mathbf{x} )=\frac{∂^2E(\mathbf{x} )}{∂\mathbf{x} ^2}=\mathbf{Q} $$

• Compatible with implicit integration.

Cons of The Quadratic Bending Model

• No longer valid if cloth stretches much.

✅方法假设面料拉伸比较小，当面料拉伸太大，\(\mathbf{\theta}\)就会改变，\(\mathbf{Q}\)就不准了。

• Not suitable if the rest configuration is not planar.
  • Cubic shell model.
  • Projective dynamics model.

After Class Reading

🔎 Bergou et al. 2006. A Quadratic Bending Model for Inextensible Surfaces. SCA.
✅ 这篇论文是在本算法上的进一步工作。

P37

The Locking Issue

So far we talked about the mass-spring model and other bending models, assuming cloth planar deformation and cloth bending deformation are independent.

Is it true? Think about a zero bending case. Can a simulator fold cloth freely?

✅ 正常来讲拉伸和弯曲是两件独立的事情。但在弹簧模型系统中，把它们耦合了。
例如纸这种无弹性的面料，会把它的弹性系数调得很大，达到无弹性的效果。但导致了它无法弯折的artifacts。
✅ 在K很大或网格分辨率低时， locking issue 会特别明显。

P38

The fundamental reason is due to a short of degrees of freedoms (DoFs).
For a manifold mesh, Euler’s formula says:#edges=3#vertices-3-#boundary_edges.
So if edges are all hard constraints, the DoFs are only: 3+ #boundary_edges.

✅ 自由度 = 变量数 - 约束数。
每个顶点有3个自由度、每条边是一个约束，因此单纯加点不会改善，但让点变密可以改善
✅ 实操套路：1. 弹簧压缩时让k比较小；2. 假设弹簧在一定长度范围内可自由活动，不受力，以上方法都不解决根本问题；3. 把自由度定义在边上不­是顶点上，但把问题搞得更复杂了。

P43

A Summary For the Day

• A mass-spring system

  • Planar springs against stretching/compression \(\quad\)- replaceable by co-rotational model
  • Bending springs \(\quad\)- replaceable by dihedral or quadratic bending
  • Regardless of the models, as long as we have \(E (\mathbf{x})\), we can calculate force \(\mathbf{f} (\mathbf{x} )=−∇ \mathbf{E} (\mathbf{x})\) and Hessian \(\mathbf{H} (\mathbf{x} )=∂E^2(\mathbf{x} )/∂\mathbf{x} ^2\). Forces and Hessians are stackable.

• Two integration approaches

  • Explicit integration, just need force. Instability
  • Implicit integration, as a nonlinear optimization problem
  • One way is to use Newton’s method, which solves a linear system in every iteration:

$$ (\frac{1}{∆t^2}\mathbf{M} +\mathbf{H} (\mathbf{x} ^{(k)}))∆\mathbf{x} =− \frac{1}{∆t^2} \mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})+\mathbf{f} (\mathbf{x} ^{(k)}) $$

• There are a variety of linear solvers (beyond the scope of this class).
• Some simulators choose to solve only one Newton iteration, i.e., one linear system per time step.

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/