Two-Way Coupling

P26

✅ 水和水中的物体相互作用，物体可以是刚体、弹性体能各种类型的物体。

The coupling between a solid and a liquid should be two-way, i.e., liquid->solid and solid->liquid.

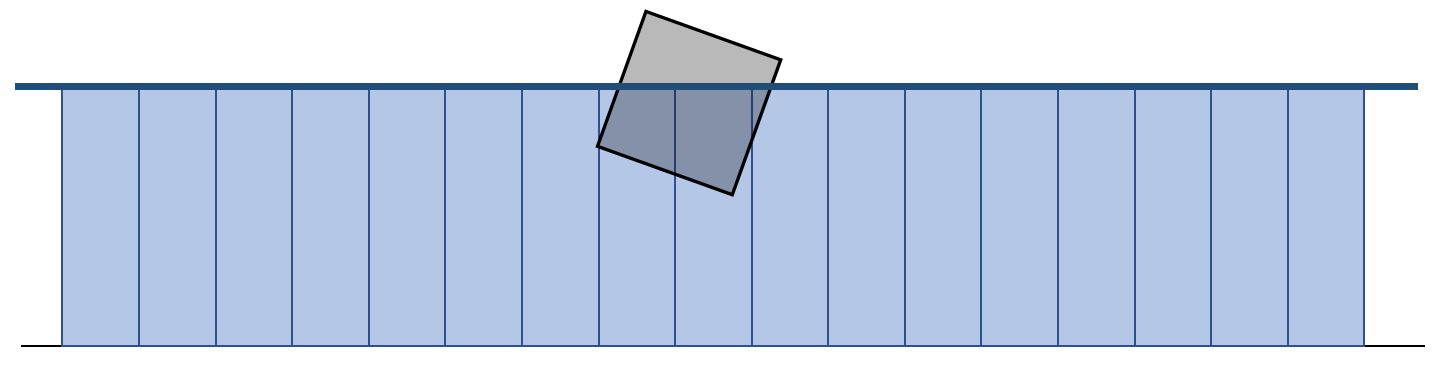
✅ 水 → 物体：浮力。物体 → 水，会把这个水柱的水排出去，此处只讲 “物体 → 水” 部分

P27

关键问题

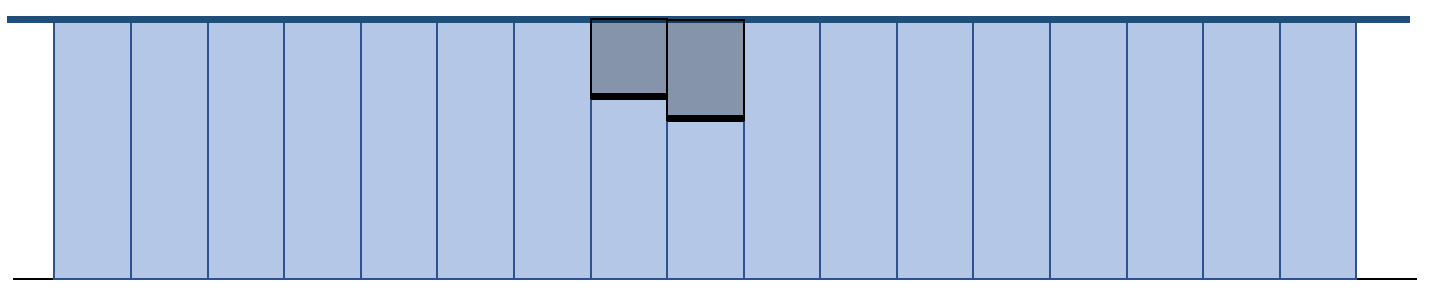
The coupling between solid and water should be two-way, i.e., water>solid and solid- >water.

The key question is how to expel water out of the gray cell regions???

P28

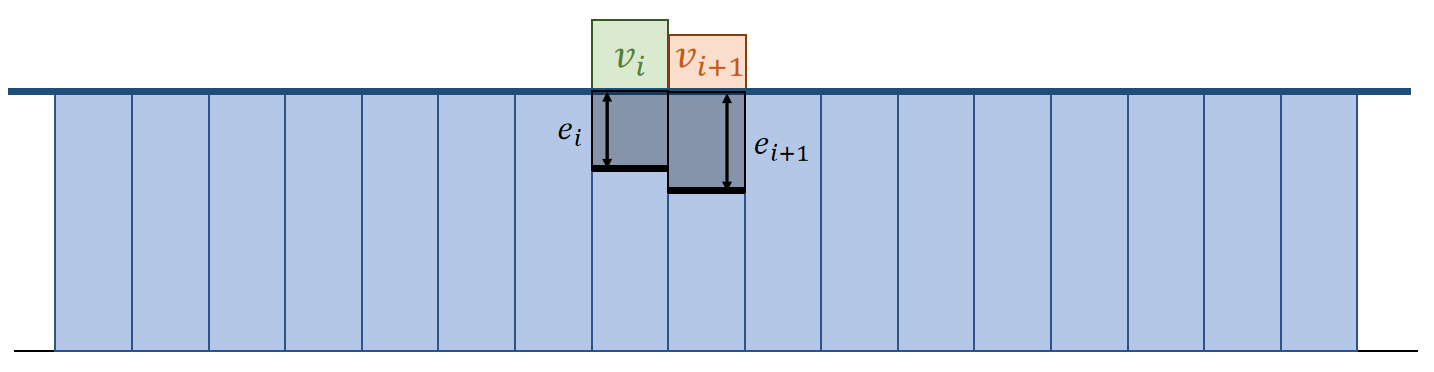
✅ 在要排的水柱上面增加一个虚拟的高度，然后正常模拟，关键是求出要加多少虚拟高度，能正好达到排出那么多水的效果。

The idea is to set up a virtual height $v_i$ , so that $ℎ_i^\text{real_new}=ℎ_i−e_i$ .

$ℎ_i−e_i=ℎ_i+β(ℎ_i−ℎ_i^{old})+α(v_{i+1}+ℎ_{i+1}+ℎ_{i−1}−2v_i−2{ℎ_i})=ℎ_i^{new}+α(v_{i+1}−2v_i)$

✅ $ℎ_i^\text{real_new}=ℎ_i−e_i$ ：下图左边格子的理想高度。

$ℎ_{i+1}−e_{i+1}=ℎ_{i+1}+β(ℎ_{i+1}−ℎ_{i+1}^{old})+α(ℎ_{i+2}+v_i+ℎ_i−2v_{i+1}−2ℎ_{i+1})=ℎ_{i+1}^{new}+α(v_i−2v_{i+1})$

✅ 公式2对应右边格子。

P29

The outcome is Poisson’s equation, with $v_i$ and $v_{i+1}$ being unknowns.

$2v_i−v_{i+1}=\frac{1}{α}(ℎ_i^{new}−ℎ_i+e_i)=b_i$

$−v_i+2v_{i+1}=\frac{1}{α}(ℎ_{i+1}^{new}−ℎ_{i+1}+e_{i+1})=b_{i+1}$

✅ 通过公式化简提取出其中的线性关系。

P30

The outcome is Poisson’s equation, with $v_i$ and $v_{i+1}$ being unknowns.

✅ 由于木块位置会变，需要解的 $v_i$ 也要改变。为了让公式统一方便计算，把图左矩阵乘法写成右边形式。公式结果不变，只是工程实现上的简化。

P31

✅ $\gamma$ 的作用：本算法显式积分，不稳定、 $\gamma$ 会让水波小很多。

P32

We estimate the floating force by the actual water expelled in every column.

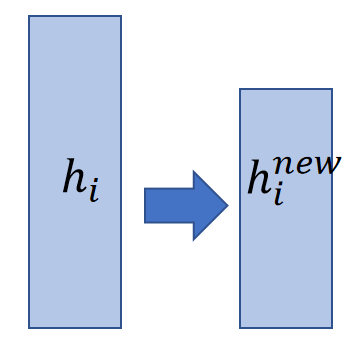
$f_i=ρg∆x(ℎ_i−ℎ_i^{new})$

Or in 3D,

$f_{i,j}=ρg∆A(ℎ_{i,j}−ℎ_{i,j}^{new})$

✅ 阿基米得定律：物体受到的浮力 = 排出去的水的重力
✅ 同时要考虑旋转和力矩。但目前旋转的效果不太好，可以考虑改进为隐式积分。
✅ 流体对方块的效果。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/