💡 旋转的表示比较独立，单独放在最后link，避免破坏整体的结构性。最后结论是混合式的积分方法。

P27

符号定义

角度

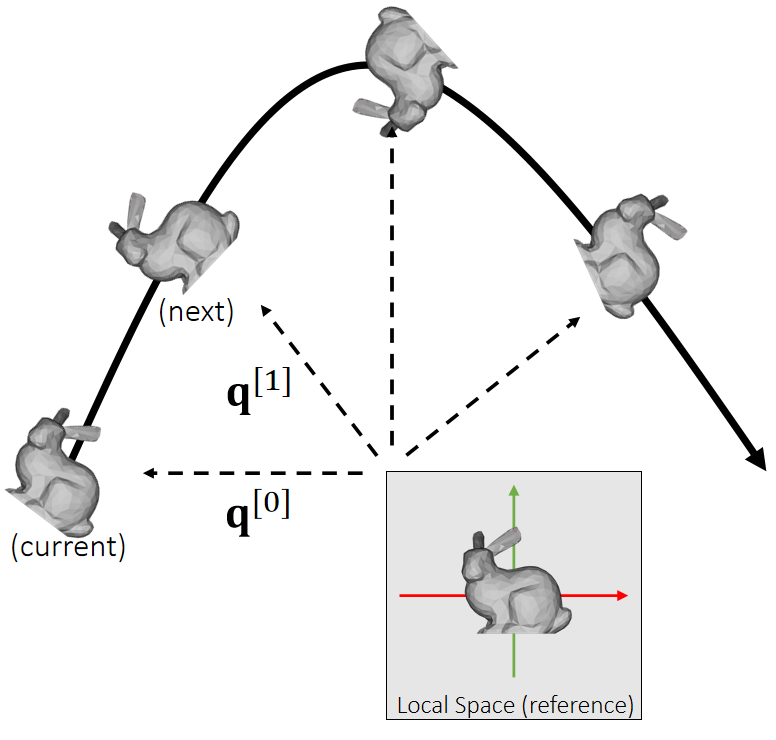
Now we choose quaternion $\mathbf{q}$ to represent theorientation, i.e., the rotation from the reference to the current.

角速度

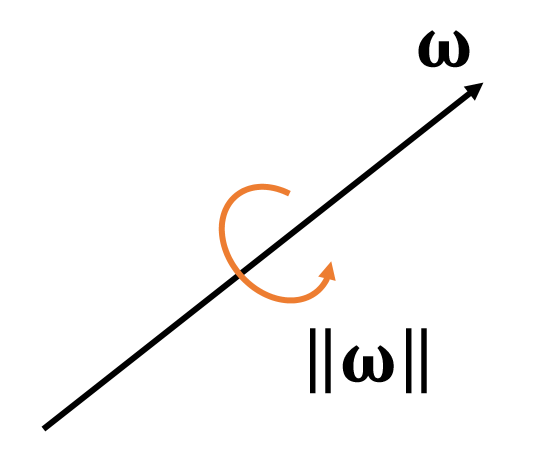
We use a 3D vector $\mathbf{\omega}$ to denote angular velocity.

$\begin{cases} \text{The direction of } \mathbf{\omega} \text{ is the axis.} \\ \text{The magnitude of } \mathbf{\omega} \text{ is the speed.} \end{cases}$

力矩 torque

A torque is the rotational equivalent of a force. It describes the rotational tendency caused by a force.

✅ Torque：力矩，造成物体旋转的趋势。类比于Force：力，造成物体运动的趋势。

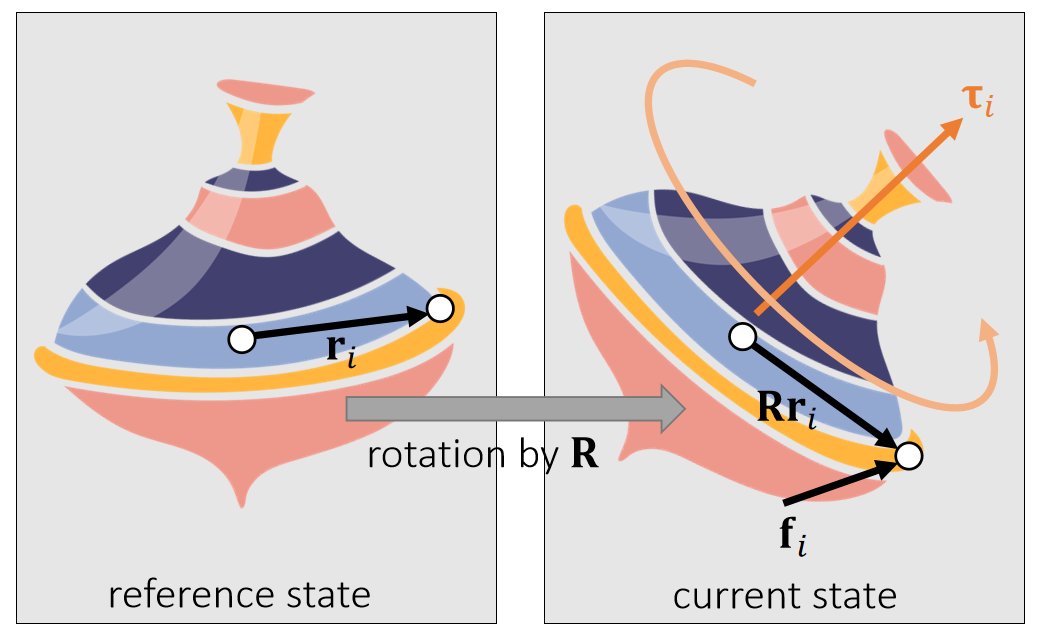
✅ $\mathbf{Rr} _i$ ：当前状态下质心到作用点的向量

$\mathbf{τ} _i$ is perpendicular to both vectors: $\mathbf{Rr} _i$ and $\mathbf{f} _i$ .

✅ 因此力矩的方向决定了旋转轴的方向，因此由叉差乘得到

$\mathbf{τ} _i$ is porportional to || $\mathbf{Rr} _i$ || and || $\mathbf{f} _i$ ||.

$\mathbf{τ} _i$ is porportional to $\sin \theta$ .
( $\theta$ is the angle between two vectors.)

✅ 力矩的大小决定旋转的快慢。

$\mathbf{τ} _i\longleftarrow (\mathbf{Rr} _i)\times \mathbf{f} _i$

inertia tensor

Similar to mass, an inertia tensor describes the resistance to rotational tendency caused by torque. But different from mass, it’s not a constant.

✅ inertia 也与自身的状态相关

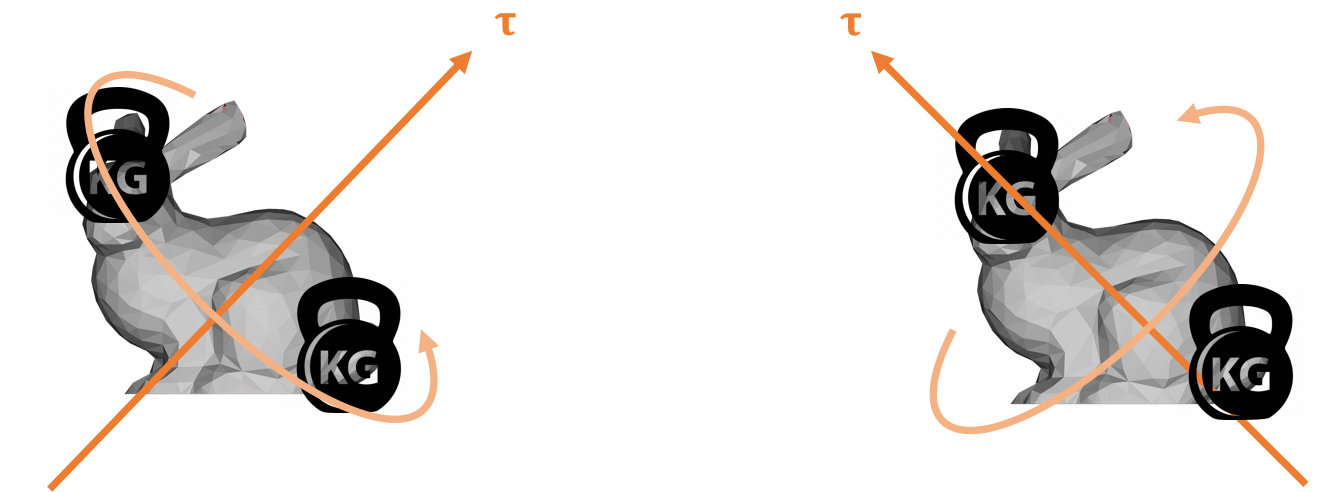
Which side receives greater resistance?

✅ 两图的力矩大小相同，但产生的旋转不同
inertia 看作是对运动的抵抗，其效果与力矩的方向有关，因此不是常数

It’s a matrix! The mass inverse is the resistance (just like mass).

✅ 用于旋转的质量不再是实数，而是矩阵，称为 Inertia 矩阵，用 $\mathbf{I}$ 来标记 Inertia 矩阵，其中 $\mathbf{I}_{ref}$ 为参考状态， $\mathbf{I}$ 为当前状态， $\mathbf{I}$ 是 $3\times 3$ 矩阵。

reference state	current state

$\mathbf{I} _{\mathbf{ref} }=\sum m_i(\mathbf{r} _i^\mathbf{T} \mathbf{r} _i\mathbf{1} −\mathbf{r} _i\mathbf{r} _i^\mathbf{T} )$ $\mathbf{1}$ is the 3-by-3 identity.	$\mathbf{I} =\sum m_i(\mathbf{r} _i^\mathbf{T}\mathbf{R} ^\mathbf{T}\mathbf{Rr} _i\mathbf{1} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$ $\quad=\sum m_i(\mathbf{Rr} _i^\mathbf{T}\mathbf{r} _i\mathbf{1R} ^\mathbf{T} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$ $\quad=\sum m_i\mathbf{R}(\mathbf{r}_i^\mathbf{T}\mathbf{r}_i\mathbf{1}−\mathbf{r}_i\mathbf{r}_i^\mathbf{T} ) \mathbf{R^T}$ $\quad=\mathbf{RI _{ref}R^T}$

reference state

current state

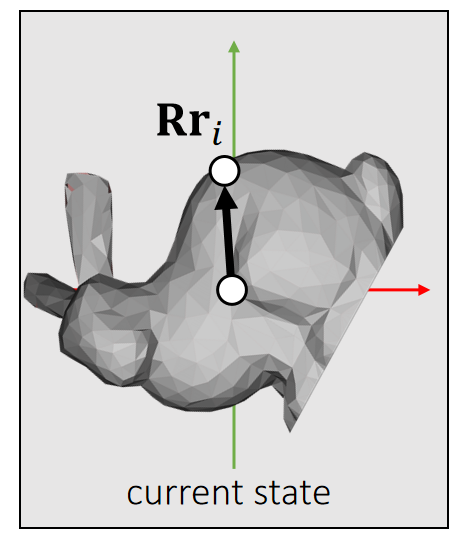$\mathbf{I} _{\mathbf{ref} }=\sum m_i(\mathbf{r} _i^\mathbf{T} \mathbf{r} _i\mathbf{1} −\mathbf{r} _i\mathbf{r} _i^\mathbf{T} )$

$\mathbf{1}$ is the 3-by-3 identity.

$\mathbf{I} =\sum m_i(\mathbf{r} _i^\mathbf{T}\mathbf{R} ^\mathbf{T}\mathbf{Rr} _i\mathbf{1} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$

$\quad=\sum m_i(\mathbf{Rr} _i^\mathbf{T}\mathbf{r} _i\mathbf{1R} ^\mathbf{T} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$

$\quad=\sum m_i\mathbf{R}(\mathbf{r}_i^\mathbf{T}\mathbf{r}_i\mathbf{1}−\mathbf{r}_i\mathbf{r}_i^\mathbf{T} ) \mathbf{R^T}$

$\quad=\mathbf{RI _{ref}R^T}$

✅ 不需要每次都根据当前状态计算，而是基于一个已经算好的ref状态的 inertia快速得出。

P29

更新法则

	Translational (linear)	Rotational (Angular)
Updafe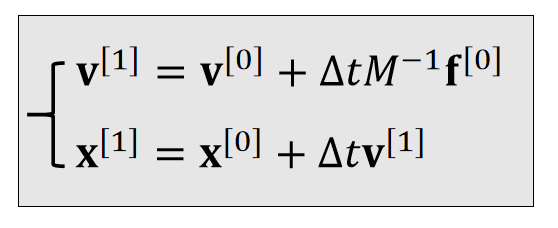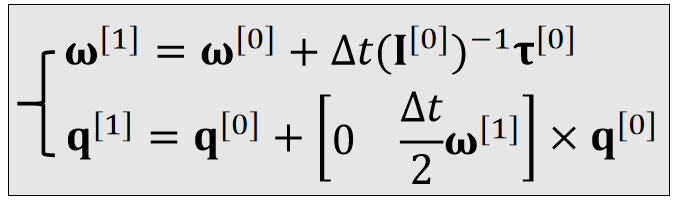
states	Velocity $\mathbf{v}$ Position $\mathbf{x}$	Angular velocity $\mathbf{ω}$ Quaternion $\mathbf{q}$
Physical Quantities	Mass $\mathbf{M}$ Force $\mathbf{f}$	Inertia $\mathbf{I}$ Torque $\mathbf{τ}$

✅ 平移： $加速度 = \frac{力}{质量}$ ，旋转： $加速度 =\frac{力矩}{\text{Inertia}}$
✅ $q$ 是四元数，代表物体的旋转状态
✅ $q_1\times q_2$ 不是叉乘，而是四元数普通乘法
✅ $\begin{bmatrix} 0 & \frac{\bigtriangleup t}{2} & w^{(1)} \end{bmatrix}$ 是一个四元数，0为实部，后面为虚部
❗ 算完 $q^{[1]}$ 的之后要对它 Normalize
🔎 由 $q^{[0]}$ 到 $q^{[1]}$ 的更新公式的推导过程见Affer Class Reading（Appendix B）
❓ 四元数相加有什么含义？

P30

Rigid Body Simulation Piplene

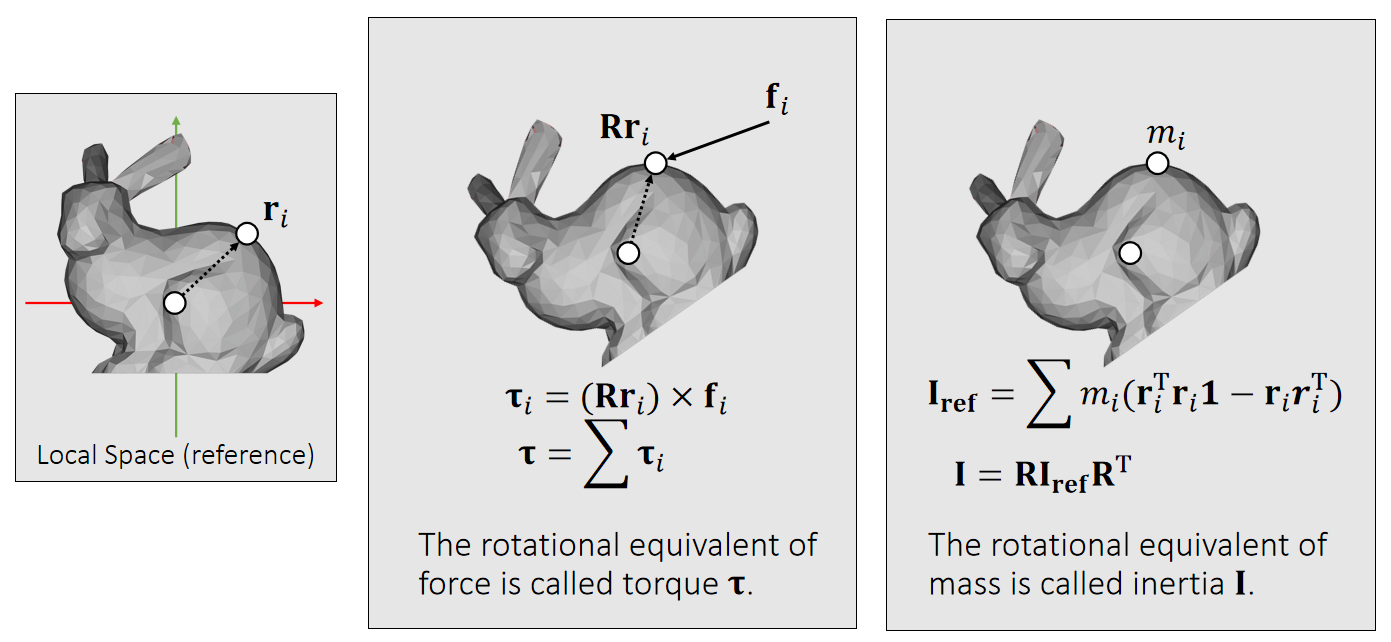
In practice, we update the same state variable $\mathbf{s} =$ { $\mathbf{v,x,\omega ,q}$ } over time.

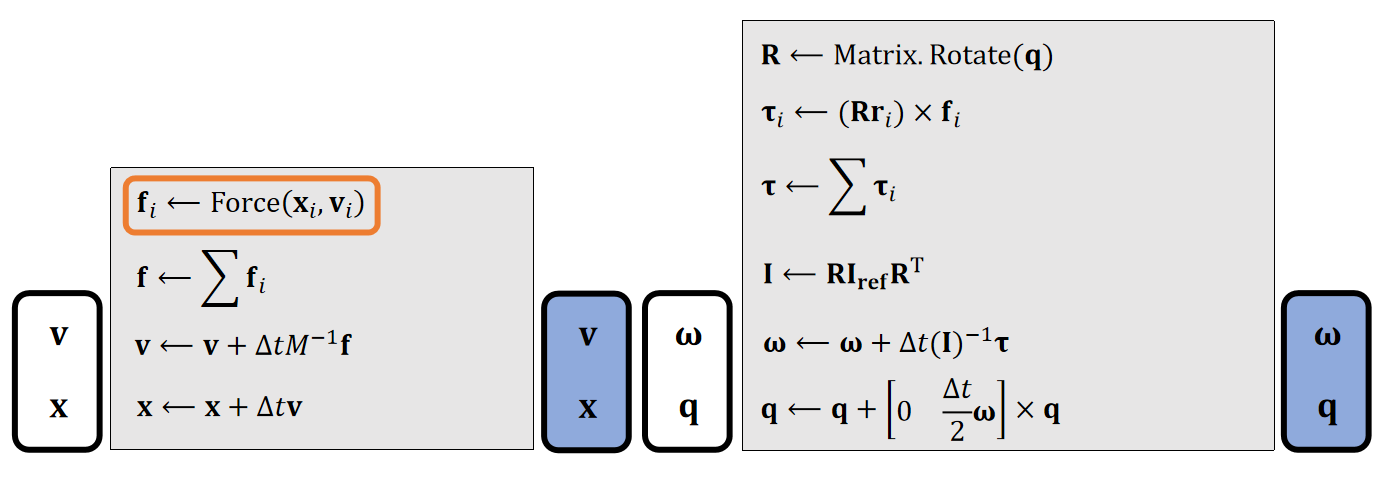
❗ Gravity doesn't cause any torque! lf your simulator does not contain any other force, there is no need to update $\mathbf{\omega}$ .

P33

After-Class Reading (Before Collision)

P35

https://graphics.pixar.com/pbm2001

❓ 建议读其中的Rigid Body Dynamics部分

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/