P13
Finite Volume Method
✅ FEM求导,FVM积分。在线性场景下,FEM和FVM本质上等价的。
✅ FVM基于力从何而来的思想。
符号定义
P14
Traction
First, let’s consider traction t: the internal force per unit length (area).
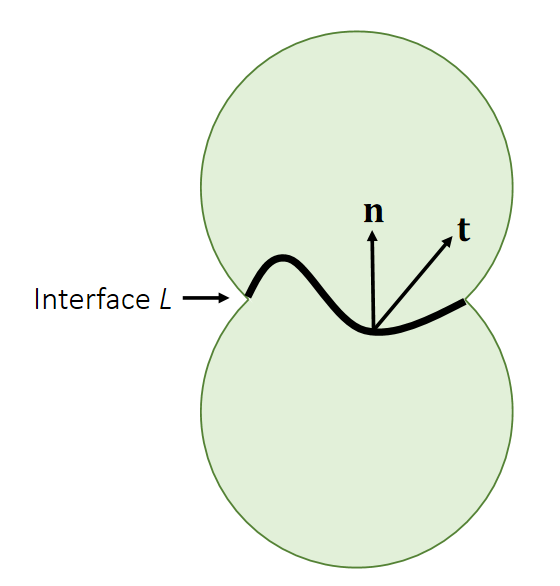
✅ 两个弹性体被界面 \(L\) 分开、求 \(L\) 上的力、
Total interface force:
$$ f\mathbf{} =\oint _L \mathbf{t} dl $$
✅ \(\mathbf{t}\)是\(L\) 上的单位面积/长度上的力。那么总的力是 \(t\) 的积分。
✅ traction 表达物体形变后会向周围施加的力。
Stress
Stress tensor \(\mathbf{σ} \) (interface normal -> traction):
$$ \mathbf{t=σn} $$
So,
$$ \mathbf{f} =\oint_{L} \mathbf{σn} dl $$
✅ \(\mathbf{σ}\) 一个3 \(\times \)3的矩阵
P15
计算FVM中的力
2D
FVM considers force calculation in an integration perspective, not a differentiation perspective.
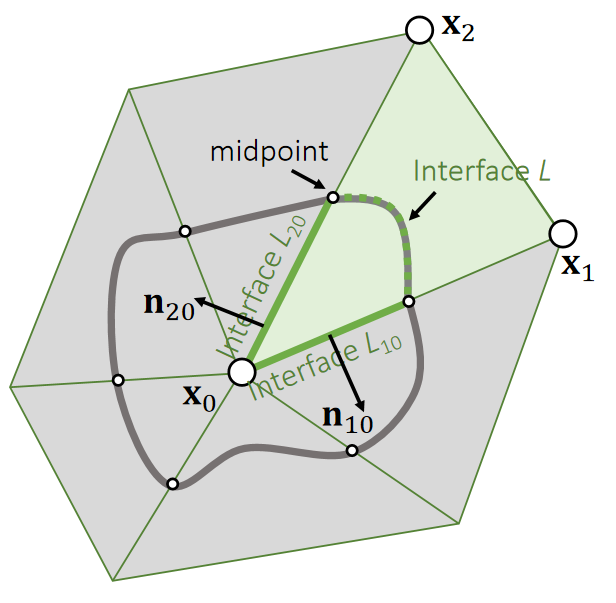
✅ \(\mathbf{X}_0\)是顶点\(\mathbf{X}_0\)附近邻域面积上的力。
Force contributed by an element:
$$ \mathbf{f}_0 =\oint _L \mathbf{σn} dl $$
✅ \(\mathbf{X}_0\)上的力是邻域面边界\(L\)上的力的积分、不考虑边界内部的力,因为认为内力为0。
✅ 仅看其中一个三角形、假设曲线经过 \(\mathbf{X}_0\mathbf{X}_1\)和 \(\mathbf{X}_0\mathbf{X}_2\)的中点。因为三角形的力对三个顶点是平均的。
Since \(\mathbf{σ}\) is constant within the element,
$$ \oint_L \mathbf{σn} dl + \oint_{L_{20}} \mathbf{σn} dl+\oint_{L_{10}}\mathbf{σn} dl=0 $$
✅ 对于封闭曲线L+L10+L20做积分,\(\int _n=0\),因此 \(\sigma \int _n=0\)
(Divergence Theorem)
We know the force is:
$$ \mathbf{f}_0 = - \oint _ {L _{20}} \mathbf{σn} _ {20} dl - \oint _ {L _{10}} \mathbf{σn} _ {10} dl = - \mathbf{σ}(\frac{||\mathbf{X} _ {20}||}{2}\mathbf{n} _ {20}+ \frac{||\mathbf{X} _ {20}||}{2}\mathbf{n} _ {10}) $$
P16
3D
✅ 三维场景是对四面体的四个面积分。
✅ 每个三角形的 stress 都不同、同一个三角形内部 stress 是常数。
In 3D, FVM works in the same way.
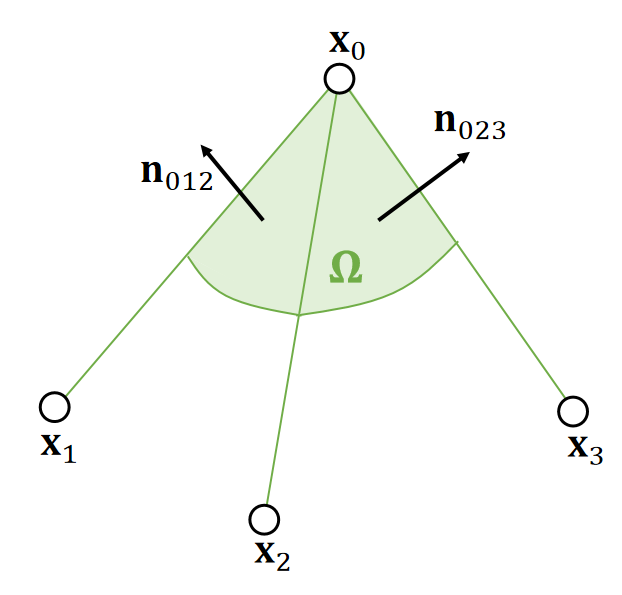
Force:
$$ \begin{array}{l} \mathbf{f} _ 0 = −\oint _ Ω \mathbf{σn} dA=−\mathbf{σ} (\frac{A _ {012}}{3}\mathbf{n} _ {012} + \frac{A _ {023}}{3}\mathbf{n} _ {023} + \frac{A _ {031}}{3}\mathbf{n} _ {031})\\ =−\frac{σ}{3}(\frac{||\mathbf{x} _ {10} \times \mathbf{x} _ {20}||}{2} \frac{\mathbf{x} _ {10} × \mathbf{x} _ {20}}{||\mathbf{x} _ {10} × \mathbf{x} _ {20}||} + \frac{||\mathbf{x} _ {20} × \mathbf{x} _ {30}||}{2}\frac{\mathbf{x} _ {20} × \mathbf{x} _ {30}}{||\mathbf{x} _ {20} × \mathbf{x} _ {30}||} +\frac{||\mathbf{x} _ {30} × \mathbf{x} _ {10}||}{2}\frac{\mathbf{x} _ {30} × \mathbf{x} _ {10}}{||\mathbf{x} _ {30} × \mathbf{x} _ {10}||})\\ =−\frac{\mathbf{σ}}{6} (\mathbf{x} _ {10} × \mathbf{x} _ {20} + \mathbf{x} _ {20} × \mathbf{x} _ {30} + \mathbf{x} _ {30} × \mathbf{x} _ {10}) \end{array} $$
❓ 遗留问题, stress 如何计算?
✅ \(f_0\)是\(\sigma n\)在绿色体截面上的积分。
✅ 类似于上一页合力为零的原理,\( \oint 截面+\oint 表面=0\)
✅ “面积/3”是因为面上的贡献均匀地分布到三个点上。
P17
计算FVM中的stress
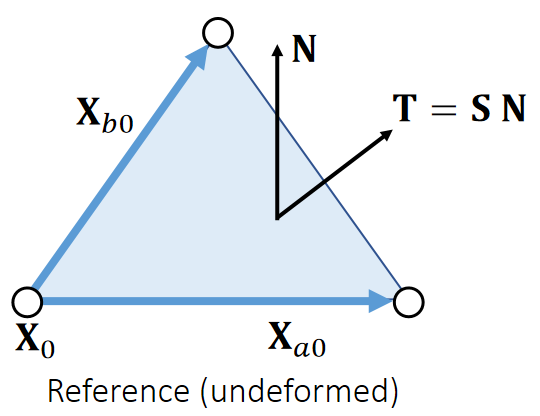
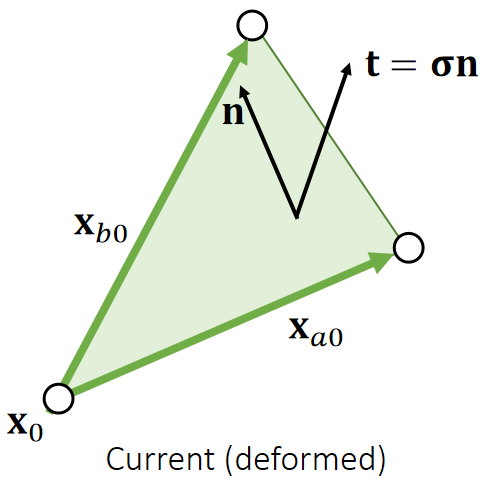
Although the use of stress tensor is the same: mapping from the interface normal to the traction, it can be defined by different configurations.
 |  |
|---|---|
| In FEM, we define the energy density \(W\) in the reference state. Therefore, this stress \(\mathbf{S}\) is a mapping from the normal \(\mathbf{N}\) to the traction \(\mathbf{T}\), both in the reference state. | In FVM, we need \(\mathbf{σ}\) to convert the normal into \(\mathbf{t}\) for force calculation. Therefore, this stress assumes the normal \(\mathbf{n}\) and the traction \(\mathbf{t}\) are in the deformed state. |
✅ 在 reference 状态下有 normal. traction 和 stress.在形变状态下也有 normal traction 和 stress.FEM 使用的是 reference 空间下的量。
P18
Different Stresses
We can now have different stresses, serving the same purpose but in different forms.

✅ FVM 需要的是 Cauchy Stress.(\(\sigma \))、上节课讲了(S)的 计算方法,需要根据(S)求(\(\sigma \)).
✅ \(P → \sigma \) 的过程没有展开讲,结论在P21
$$ S=J\sigma=PF^\tau $$
$$ P=J\sigma F^{-\tau } $$
Lecture [21:35]
P19
P与\(\sigma \)的关系:Area Weighted Normals
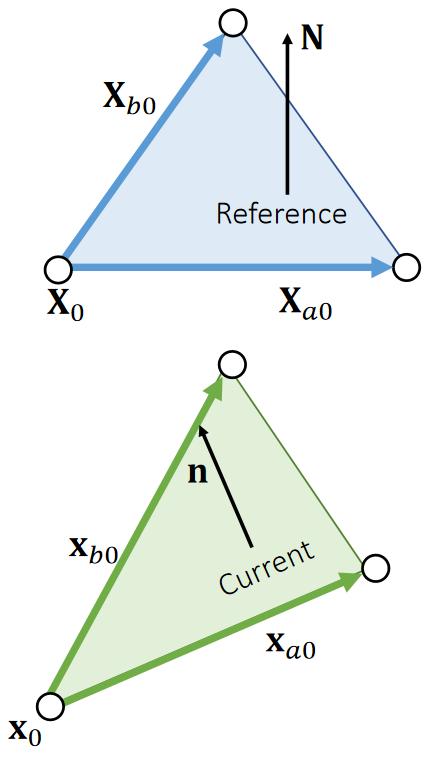
Now let’s figure out the relationship between \(A^{\mathrm{ref} }\mathbf{N}\) and \(A\mathbf{n}\), the two area weighted normals.
$$ 2A^{\mathrm{ref} }\mathbf{N} =\mathbf{X} _ {a0}×\mathbf{X} _ {b0} $$
$$ \begin{array}{l} 2A\mathbf{n} =\mathbf{x} _ {a0}×\mathbf{x} _ {b0}=\mathbf{FX} _{a0} × \mathbf{FX} _ {b0} = (\mathbf{UDV^TX} _ {a0}) × (\mathbf{UDV^TX} _ {b0}) \\ \quad\quad=\mathbf{U} ((\mathbf{DV^TX} _ {a0}) × (\mathbf{DV^TX} _ {b0})) \\ \quad\quad=\mathbf{U} \begin{bmatrix} d_1d_2& \Box & \Box \\ \Box & d_0d_2 & \Box \\ \Box & \Box &d_0d_1 \end{bmatrix} ((\mathbf{V^TX} _ {a0})×(\mathbf{V^TX} _ {b0}))\\ \quad\quad=\mathbf{U} \begin{bmatrix} d_1d_2& \Box & \Box \\ \Box & d_0d_2 & \Box \\ \Box & \Box &d_0d_1 \end{bmatrix} \mathbf{V^T} (\mathbf{X} _ {a0} × \mathbf{X} _ {b0})\quad=d_0d_1d_2\mathbf{U} \begin{bmatrix} 1/d_0& \Box & \Box \\ \Box & 1/d_1 & \Box \\ \Box & \Box &1/d_2 \end{bmatrix} \mathbf{V^T} (\mathbf{X} _ {a0}×\mathbf{X} _ {b0}) \\ \quad\quad=\mathrm{det} (\mathbf{F} )\mathbf{F} ^{−\mathbf{T}}(\mathbf{X} _ {a0}×\mathbf{X} _ {b0})=\mathrm{det} (\mathbf{F} )\mathbf{F} ^{−\mathbf{T}}(2A^\mathrm{ref}\mathbf{N}) \end{array} $$
P20
Now we know: \(A\mathbf{n} =\mathrm{det} (\mathbf{F})\mathbf{F^{−T}} (A^{\mathrm{ref}}\mathbf{N} )\).
We also know the force can be calculated using two different stresses:
$$ \mathbf{f} =−\frac{1}{3} {\textstyle \sum {A^{\mathrm{ref} }}}\mathbf{PN} =−\frac{1}{3}\sum A\mathbf{σn} $$
Therefore, we get:
$$ \mathbf{P} (A^{\mathrm{ref} }\mathbf{N} )=\mathbf{σ} \mathrm{det} (\mathbf{F} )\mathbf{F^{−T}} (A^{\mathrm{ref} }\mathbf{N} ) $$
$$ \mathrm{det} ^{−1}(\mathbf{F} )\mathbf{PF^T=σ} $$
P21
结论
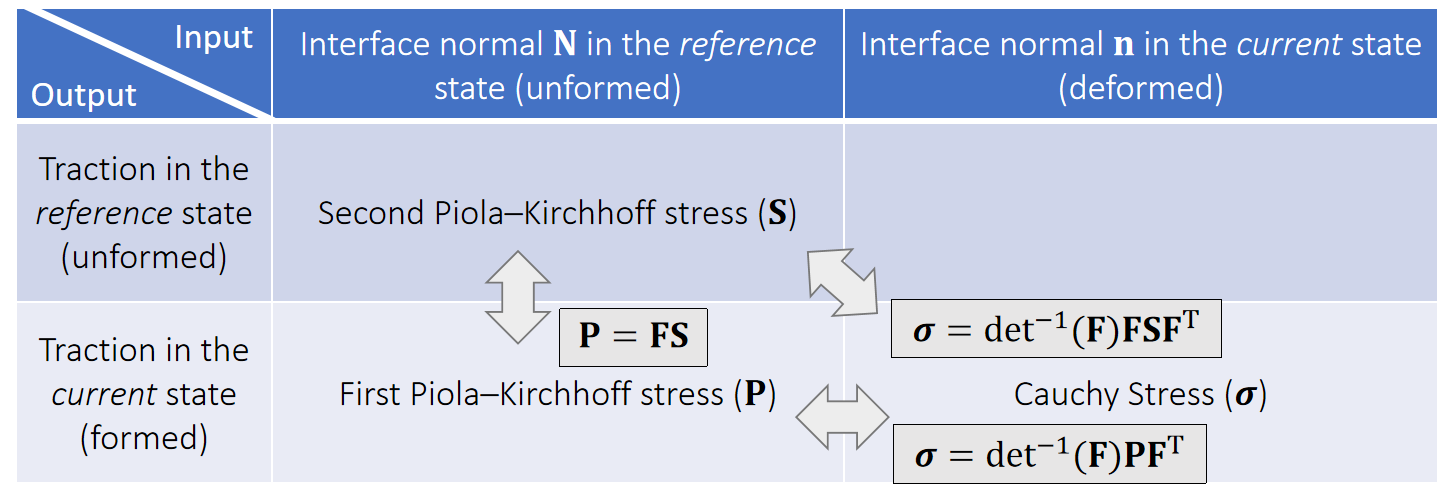
We can now have different stresses, serving the same purpose but in different forms.
P22
根据stress算出力
The previous analysis suggests we can use reference normals instead.
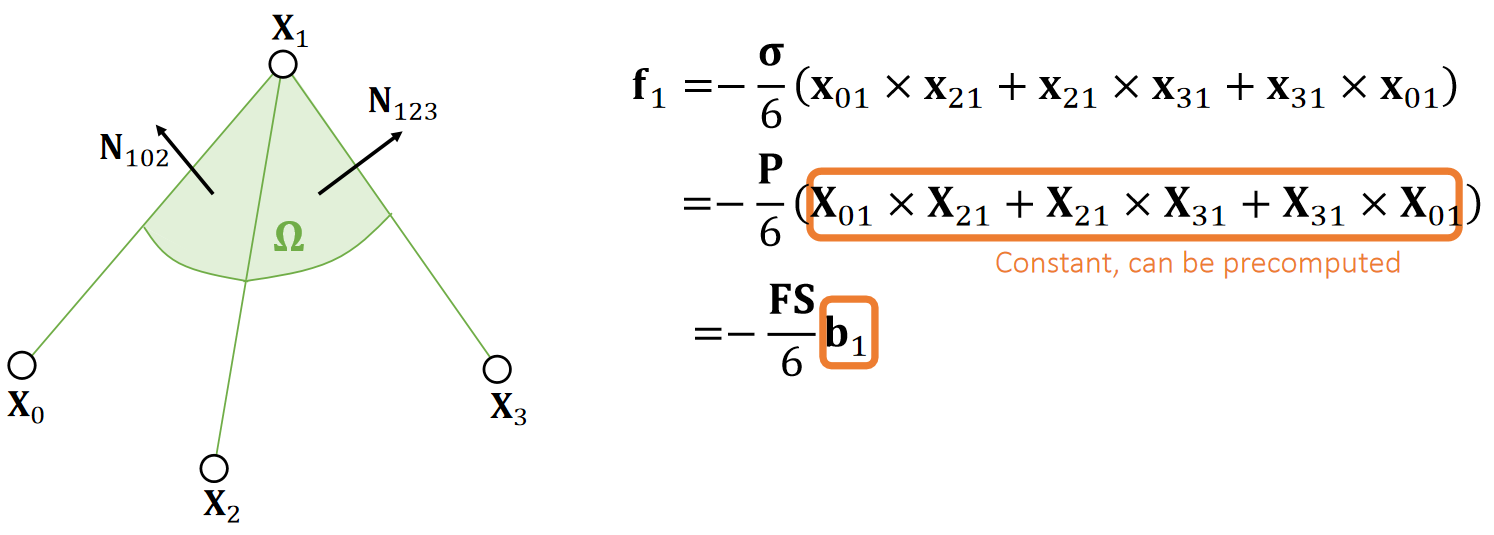
Second Piola–Kirchhoff stress:
\(\mathbf{S} =\frac{∂W}{∂\mathbf{G}}\), as in previous FEM formulation
✅ 第一行公式:用 deformed position 计算 deformed position. 第二行公式:用 ref position 计算 deformed position, 因此直接把\(\sigma \)换成 \(\mathbf{P} \) 就可以。
✅ 好处:ref position 是常数,可以做预计算、并存储为\(b_1\).
✅ F:deformation gradient.见P5
✅ 用三种不同定义的 stress 来算力、目的是得到计算最友好的公式
✅ 此处内容涉及材料力学、
P23
关于b1
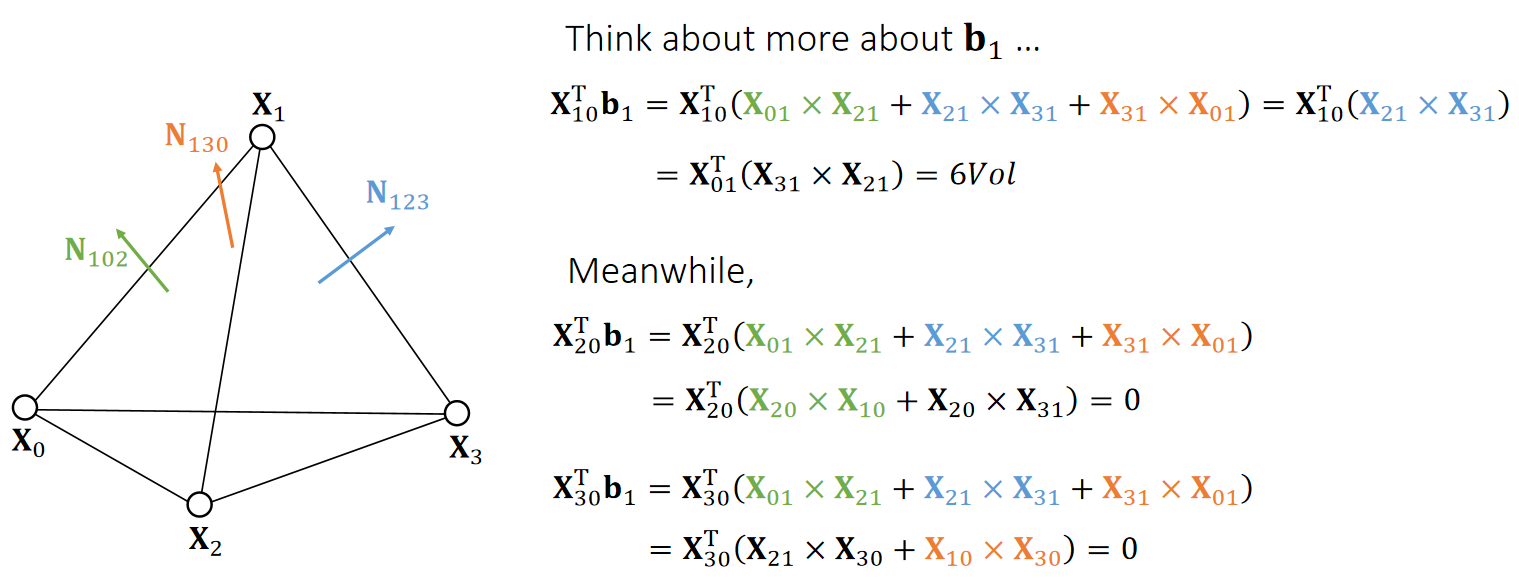
✅ 问: \(\mathbf{X}_ {20}^\mathbf{T} b_1\)的计算公式中、绿色的\(\mathbf{X}_ {01}×\mathbf{X} _ {21}\)怎么变成了\(\mathbf{X}_ {20}\times \mathbf{X}_ {10}\)?下面的\(\mathbf{X}_ {30}^\mathbf{T} b_1\),也一样。
答:因为\(\mathbf{X}_o,\mathbf{X}_1,\mathbf{X}_2\)是同一个三角形上的顶点,任意两条边做cross都是一样的,处理好正负就好了。
也可以用cross的乘法分配律得出相同的结论
P24
Therefore, We get:
$$ \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^\mathbf{T} \mathbf{b} _1=\begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^\mathbf{T}(\mathbf{X} _{01}×\mathbf{X} _{21}+\mathbf{X} _{21}×\mathbf{X} _{31}+\mathbf{X} _{31}×\mathbf{X} _{01})=\begin{bmatrix} 6Vol\\ 0\\ 0 \end{bmatrix} $$
$$ \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^\mathbf{T} \mathbf{b} _2=\begin{bmatrix} 0\\ 6Vol\\ 0 \end{bmatrix} $$
$$ \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^\mathbf{T} \mathbf{b} _3=\begin{bmatrix} 0\\ 0\\ 6Vol \end{bmatrix} $$
$$ \begin{bmatrix} \mathbf{b} _{1} & \mathbf{b} _{2} &\mathbf{b} _{3} \end{bmatrix}^\mathbf{T} =6Vol\begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^{-\mathbf{T}}\\ \quad\quad=\frac{1}{\mathrm{det}( \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^{-1})} \begin{bmatrix} \mathbf{X} _{10} & \mathbf{X} _{20} &\mathbf{X} _{30} \end{bmatrix}^{-\mathbf{T}} $$
P25
A Quick Summary
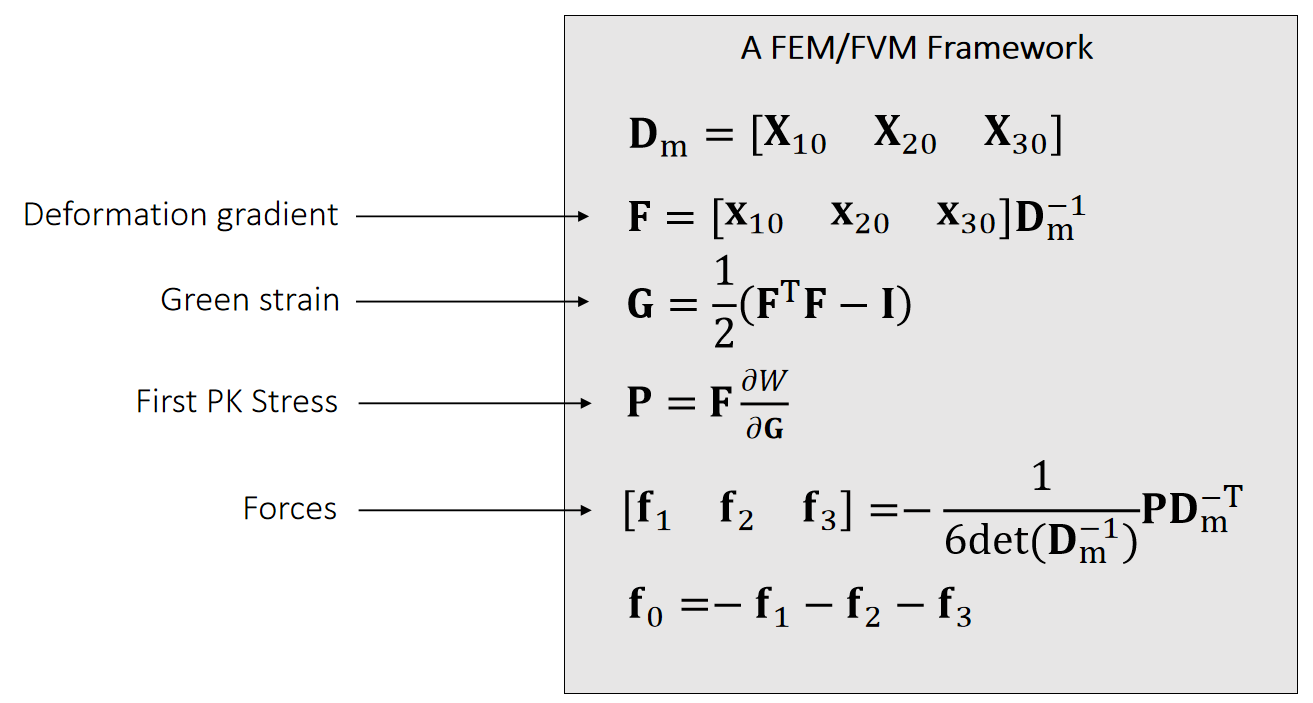
✅reference 状态下,\(F=I,G=0,P=0,f=0\)
P26
After-Class Reading
重点推荐:
Teran et al. 2003. Finite Volume Methods for the Simulation of Skeleton Muscles. SCA.
✅ 这篇论文重点推荐,但论文中的公式与 PPT 中的不完全一样. PPT 上的又进一步简化。
Optional
Volino et al. 2009. A Simple Approach to Nonlinear Tensile Stiffness for Accurate Cloth Simulation. TOG.
✅ 2D有限元
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/