P28

Hyperelastic Models

✅ 前面的内容，都假设使用 StVK 材料、优点是简单；缺点是无法处理反转。因此在材料力学中不常用。
Hyperplasia 利用能量密度(W)、提供一个从 Strain (G) 到 Stress (S)的映射

跳过

P29

First Piola–Kirchhoff stress

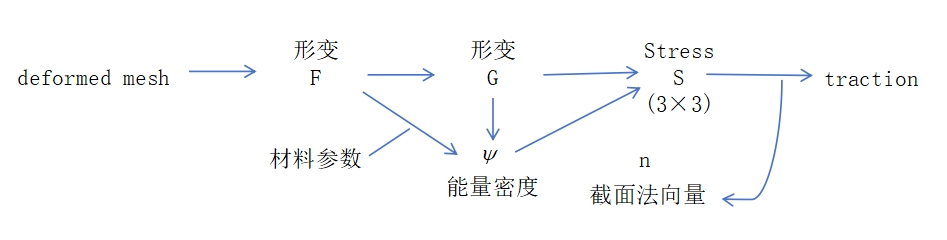
We treat the first Piola–Kirchhoff stress tensor $\mathbf{P}$ as a function of deformation gradient $\mathbf{F}$:

$$\mathbf{f} _0= −\frac{\mathbf{P} (\mathbf{F} )}{6}(\mathbf{X} _{10}×\mathbf{X} _{20}+\mathbf{X} _{20}×\mathbf{X} _{30}+\mathbf{X} _{30}×\mathbf{X} _{10})$$

It converts an interface normal $\mathbf{N}$ in the reference state to a traction $\mathbf{t}$ in the deformed state.

$$\mathbf{t}=\mathbf{P} (\mathbf{UDV^T} )\mathbf{N}$$

✅ 没讲，

P30

Rotation-Invariance

The stress tensor $\mathbf{P}$ is rotation-invariant to $\mathbf{U}$:

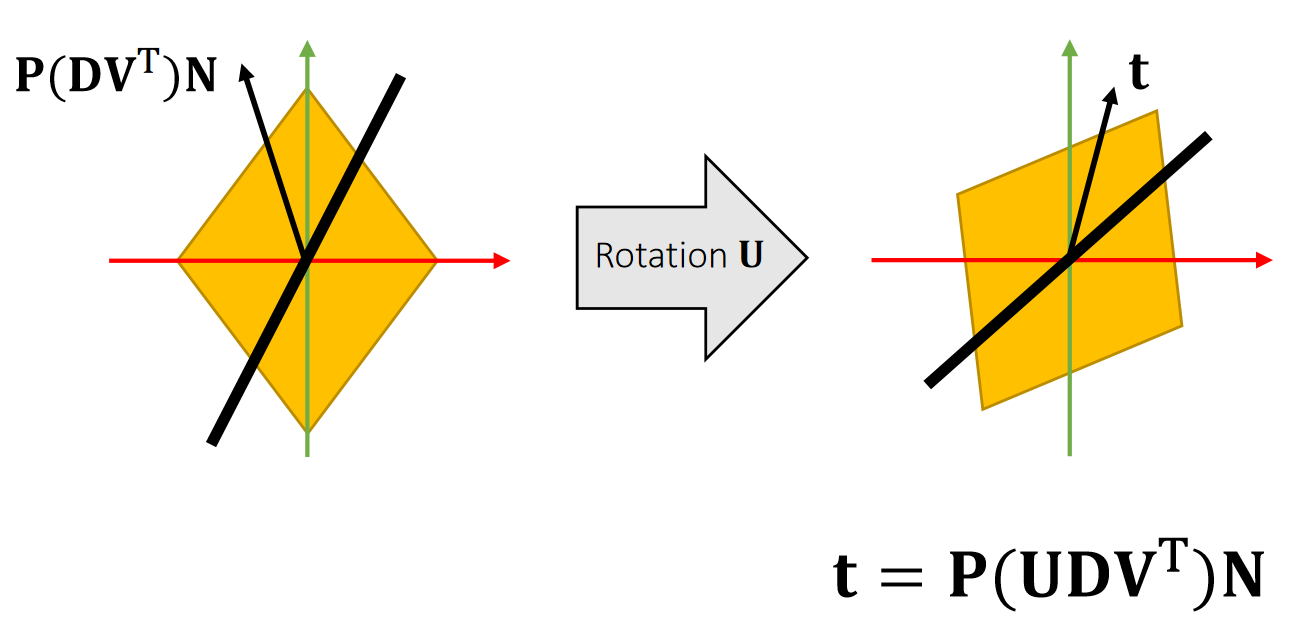
$$\mathbf{P} (\mathbf{UDV^T} )=\mathbf{UP} (\mathbf{DV^T} )$$

✅ 没讲，

P31

Isotropic Materials

The stress tensor $\mathbf{P}$ is rotation-invariant to $\mathbf{U}$:

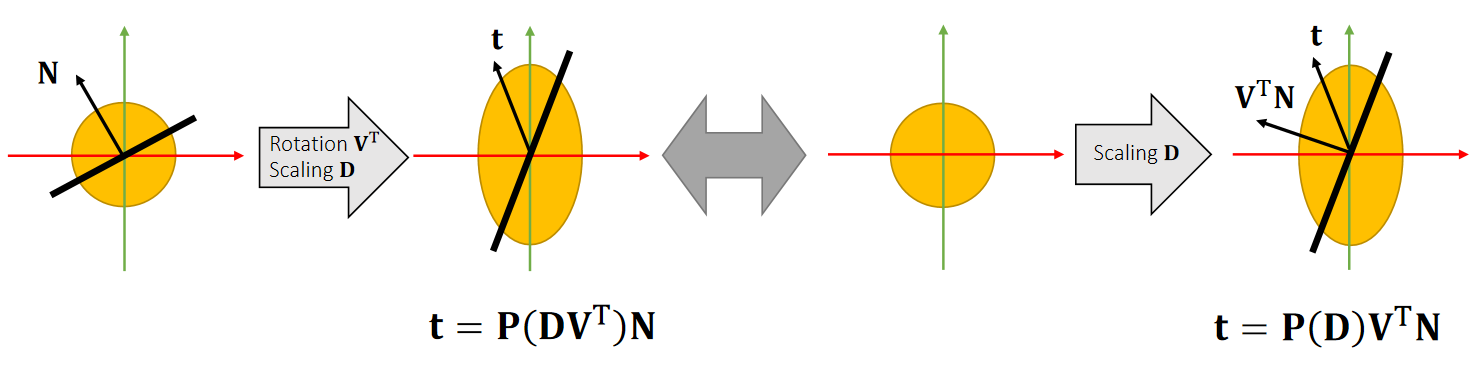
$$\mathbf{P} (\mathbf{DV^T} )=\mathbf{P} \mathbf{(D)V^T}$$

✅ 没讲，

P32

Isotropic Materials

Isotropic Materials：各向同性材料

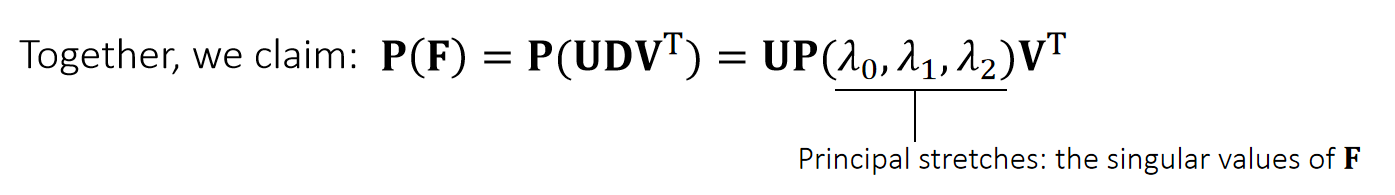
✅ 符号解释：$\mathbf{P}$：First Piola Stress、 $\mathbf{F}$：Deformation Gradient
✅ 各向同性公式认为：$\mathbf{P}$ 是关于 $\mathbf{F}$ 的函数
✅ 对F做 $\mathbf{SVD}$ 分解可得到 $\mathbf{UDV^T}$，其中$D$是对角矩阵、其对角元素描述了三个方向的拉伸的量、把公式中的旋转分量剔除掉、 $\mathbf{P}$ 只与 Principal stretches 有关。

In many literatures, people parameterize $\mathbf{P} (I_\mathbf{C},II_\mathbf{C},III_\mathbf{C} )$ by principal invariants, for:

$$I_\mathbf{C} =\mathrm{trace} (\mathbf{C} )=λ_0^2+λ_1^2+λ_2^2$$

$$III_\mathbf{C} =\mathrm{det} (\mathbf{C} ^2)=λ_0^4+λ_1^4+λ_2^4$$

$$II_\mathbf{C} =\frac{1}{2} (\mathrm{trace} ^2(\mathbf{C} )−\mathrm{trace} (\mathbf{C} ^2))=λ_0^2λ_1^2+λ_0^2λ_2^2+λ_1^2λ_2^2$$

$\mathbf{C=U^TU}$ is the right Cauchy-Green deformation tensor.

✅ $I_c、 II_c、 III_c$ 的定义是基于材料学、数学的先验知识

P33

Isotropic Models

✅ 材料力学中更常用 neo-Hookean
✅Fung常用来模拟人体组织。

P34

计算P

Anyway, we still use the principal stretches for computation:

$$\mathbf{P} (λ_0,λ_1,λ_2)=\begin{bmatrix} \frac{∂W}{∂λ_0} & \Box &\Box \\ \Box & \frac{∂W}{∂λ_1} & \Box \\ \Box & \Box &\frac{∂W}{∂λ_2} \end{bmatrix}$$

And we compute the first Piola-Kirchhoff stress as:

$$\mathbf{P} = \mathbf{UP} (λ_0,λ_1,λ_2)\mathbf{V} ^\mathbf{T}$$

P35

A Quick Summary

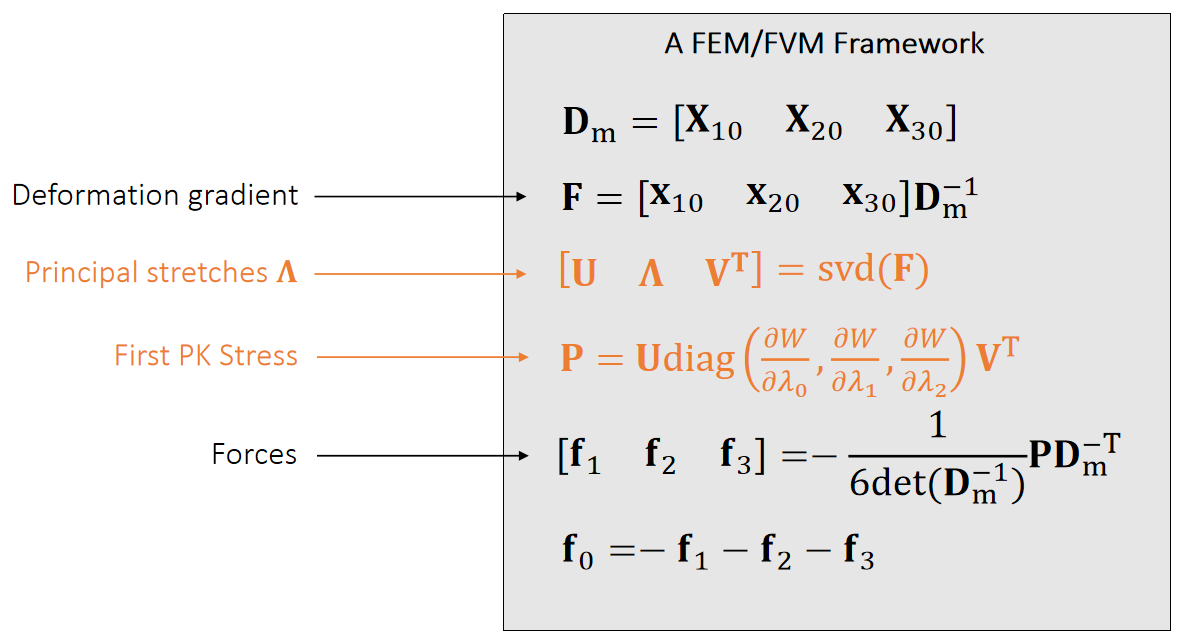
✅ 主要是算P的方法不同

P36

The Limitation of StVK

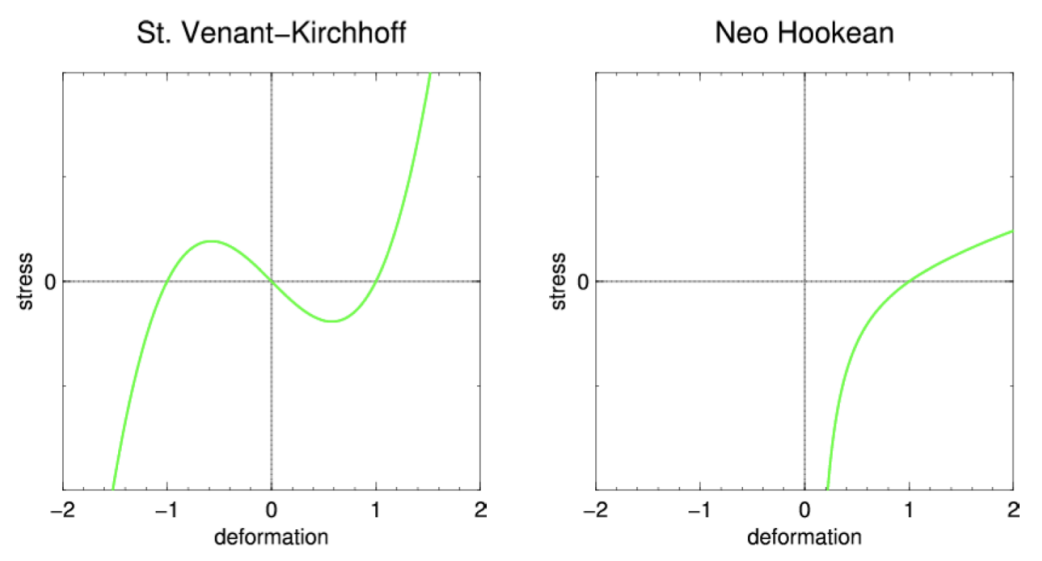
Irving et al. 2004. Invertible Finite Elements For Robust Simulation of Large Deformation. SCA

✅ 纵轴是力、横轴长度为弹簧长度、参考长度是1， 因此横轴为1时纵轴为0. 横轴 > 1 代表拉伸、拉伸越大代表力越大。但压缩时， $StVK$ 表现出的力不对，且当弹簧（四面体）反转以后，力也会反转，这种表现也不对，因为最后会停在横轴-1的状态上。

P37

✅ Poison Effect： 弹性体往上拉时两边会凹进去，本质原因是保体积。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/