P16

Volume Preservation

We want the volume to stay the same. Suppose that \(\sum ℎ_i(t)=\sum ℎ_i(t−∆t)=V\). But,

$$ ℎ_i(t_0+∆t)=2ℎ_i(t_0)−ℎ_i(t_0−∆t)+\frac{∆t^2ℎ_i}{∆x^2ρ}(P_{i+1}+P_{i−1}−2P_i) $$

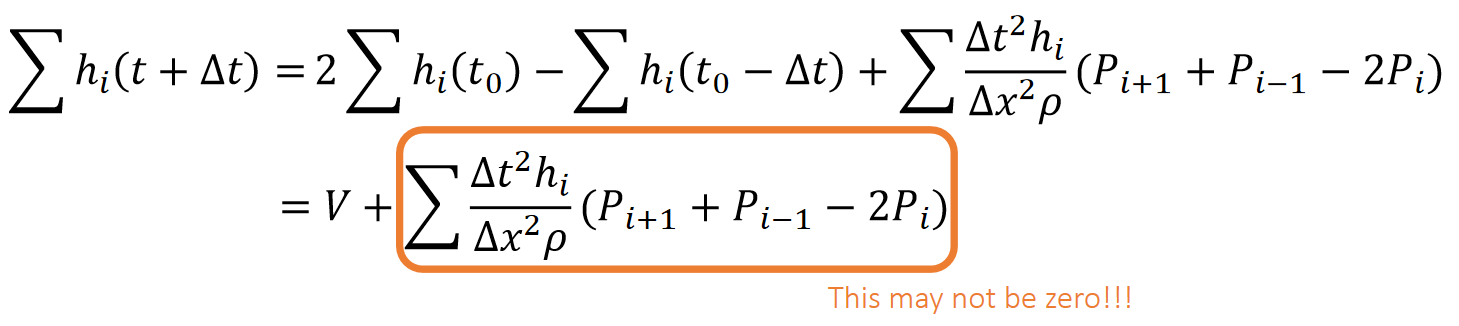
✅ 体积会变大还是变小，取决于桔色项，但很难保证这一项是0.

P17

Volume Preservation – Solution 1

✅ 保证 \(h_i\) 和 \(h_{i+1}\)的交换的水量相等、因此保体积
✅ 把\(h_{i-1}\)与\(h_i\)的交换和\(h_i\)与\(h_{i+1}\)的交换拆开。即：
（1）把\((P_{i+1}+P_{i−1}−2P_i)\)拆成\(P_{i−1}−P_i\)和\(P_{i+1}−P_i\)
（2）把\(h_i\)拆成\(\frac{h_{i-1}+h_i}{2}\)和\(\frac{h_{i+1}+h_i}{2}\)
✅ 直观理解：对每个水柱而言，流入的量和流出的量是等价的。

P18

🔎 Kass and Miller. 1990. Rapid, Stable Fluid Dynamics for Computer Graphics. Computer Graphics.

P19

Volume Preservation – Solution 2

An easier way to preserve volume is to simply assume \(h_i\) in the right term is constant.

P20

Pressure

P21

Viscosity

Like damping, viscosity tries to slow down the waves.

✅ Viscosity: 粘滞，相当于流体的阻尼。

P22

Algorithm

$$\text{A Shallow Wave Simulator}$$ For every cell \(i\) $$ℎ_i^{new}←ℎ_i+β(ℎ_i−ℎ_i^{old})\\ ℎ_i^{new}←ℎ_i^{new}+α(ℎ_{i−1}−ℎ_i)\\ ℎ_i^{new} ←ℎ_i^{new}+α(ℎ_{i+1}−ℎ_i)\\$$ For every cell \(i\) $$ℎ_i^{old}←ℎ_i\\
ℎ_i←ℎ_i^{new}$$

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/