Vector: Basics

定义

An (Euclidean) vector: A geometric entity endowed with magnitude and direction.

$$ \mathbf{P} =\begin{bmatrix} p_x\\ p_y\\ p_z\\ \end{bmatrix}\in \mathbf{R} ^3 $$

$$ \mathbf{o} =\begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix} $$

The vector p is defined with respect to the origin o.

坐标系

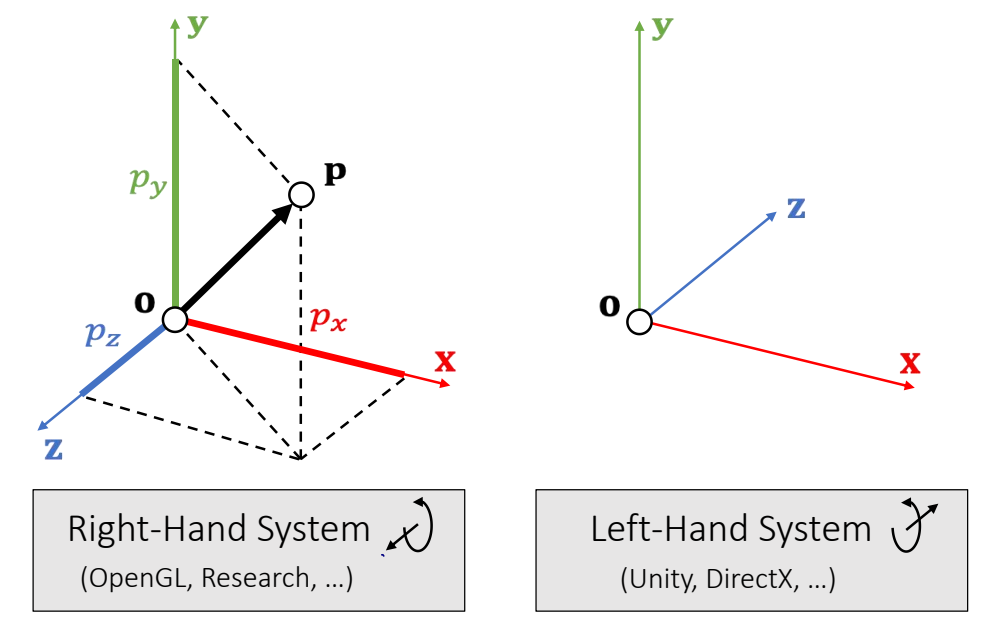
✅ 用黑来区分，矢量：黑体小写；标量：斜体；矩阵：黑体大写；

The choice of a right-hand or left-hand system is largely due to:
the convention of the screen space.

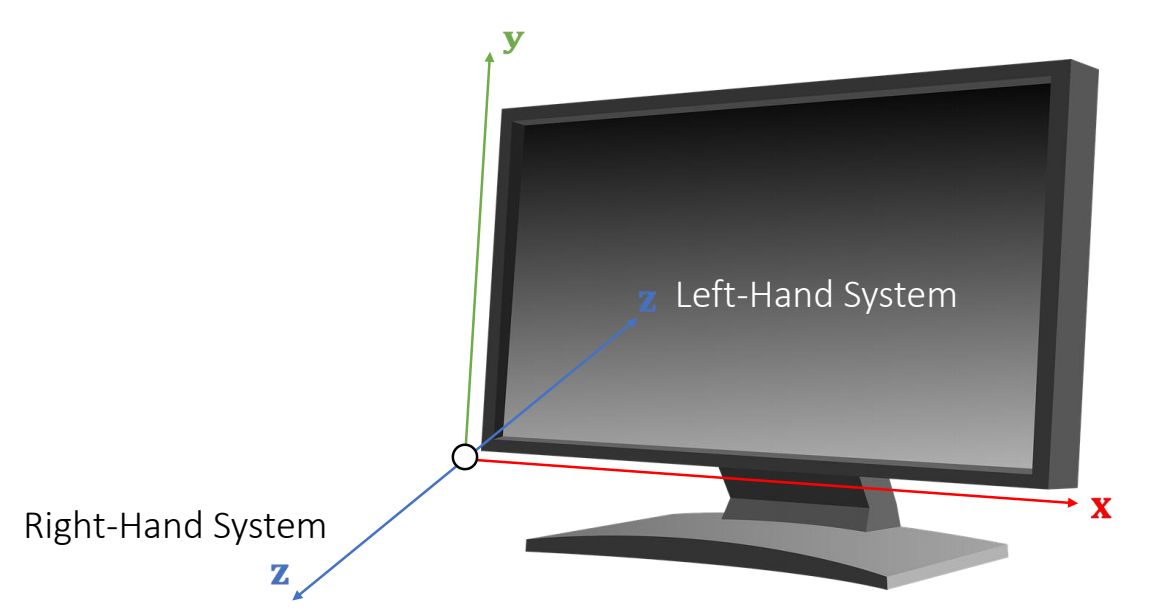
✅ 左手坐标系，E轴正方向朝屏幕内，好处是物体坐标 x、y、z 都是正值。右手系统的物体都在E轴负方向。

Stacked Vector

Vectors can be stacked up to form a high-dimensional vector, commonly used for describing the state of an object.

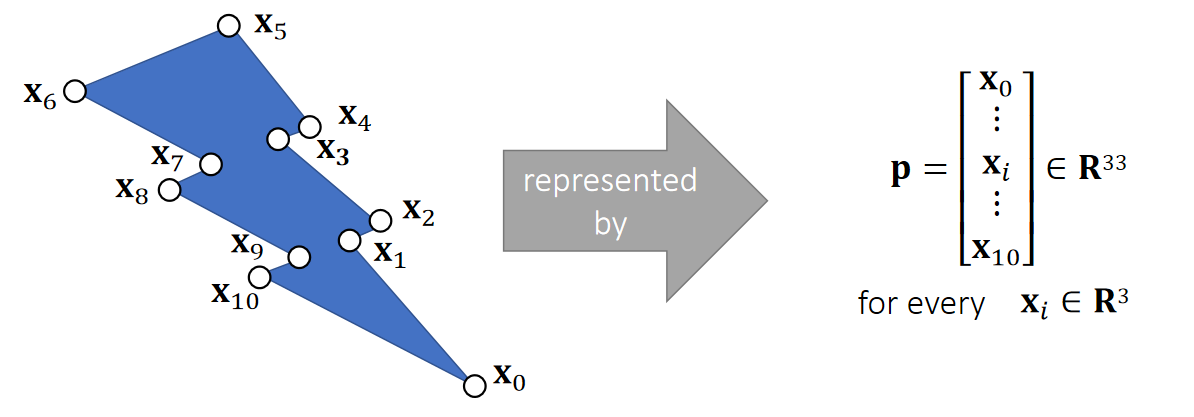
Not a geometric vector,but a stacked vector.

Vector Arithematic: Addition and Subtraction

$$ \mathbf{p\pm q=} \begin{bmatrix} p_x\pm q_x\\ p_y\pm q_y\\ p_z\pm q_z\\ \end{bmatrix} $$

$$ \mathbf{p+q=q+p} $$

Addition is commutative.

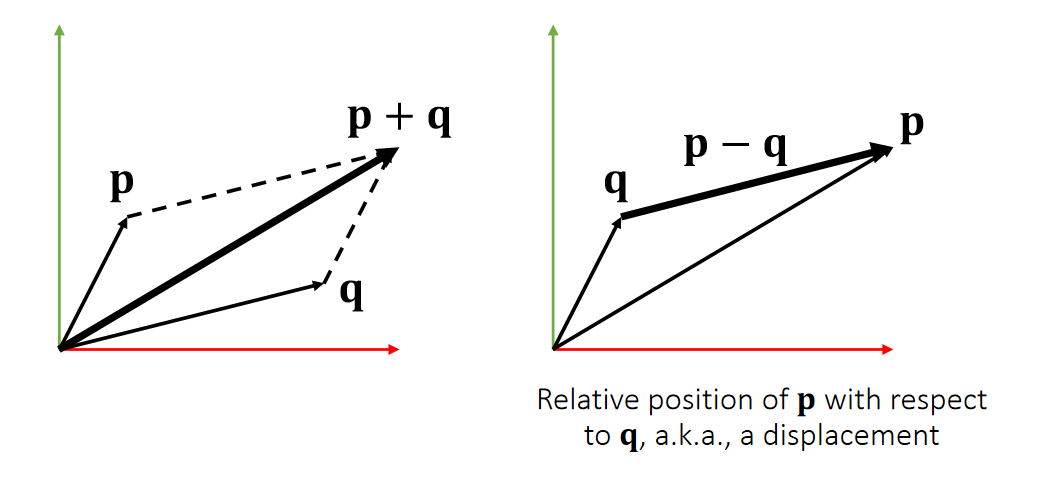
Geometric Meanings

Example 1: Linear Representation

A (geometric) vector can represent a position, a velocity, a force, or a line/ray/segment.

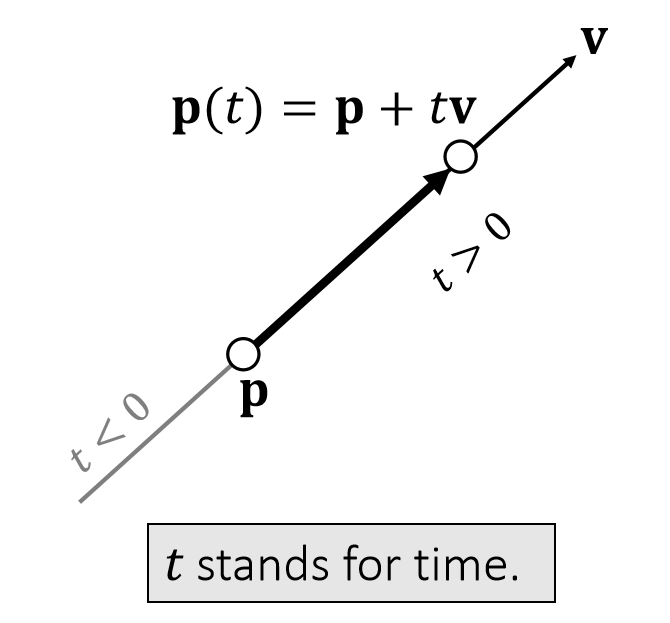
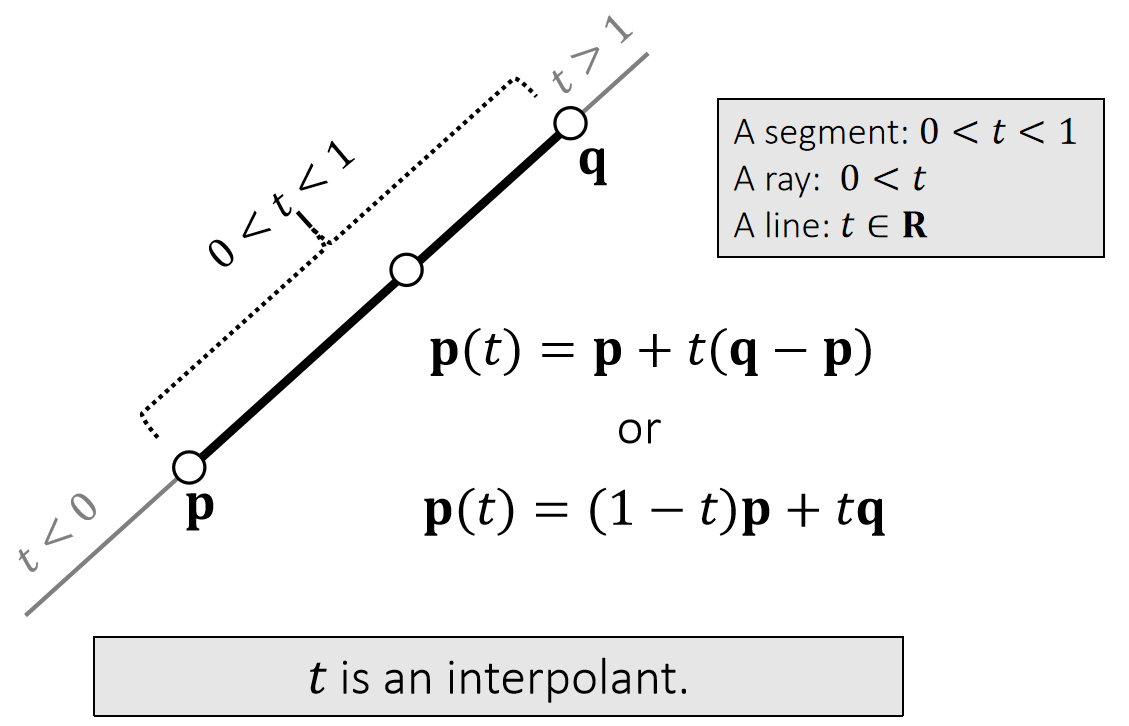
✅ 图2。同一个公式，对$t$做不同的约束，可以定义不同的东西。
$\mathbf{P}(t)$ 是 $\mathbf{P}$ 和 $\mathbf{q}$ 的 blend

Vector Norm

A vector norm measures the magnitude of a vector: its length.

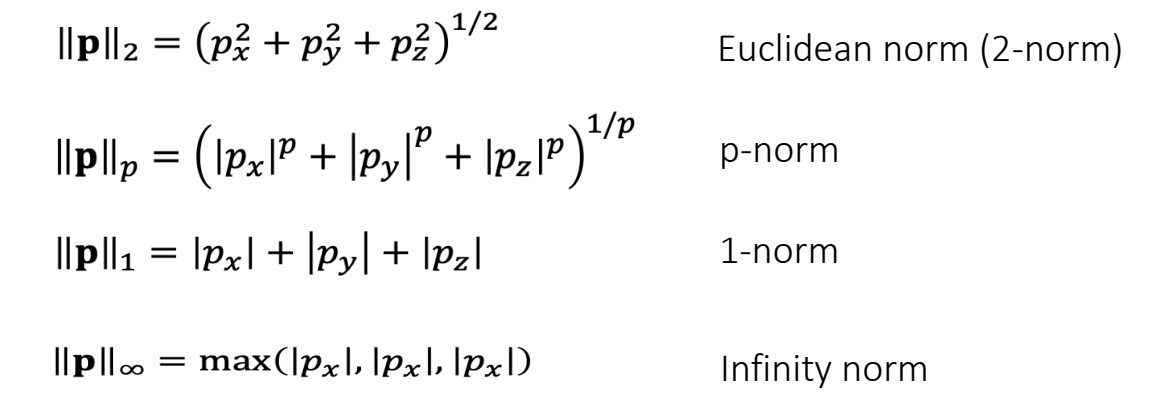
✅ L1-Norm 又称为曼哈顿的距离。没写下标一般默认L2-Norm

Vector Norm: Usage

Distance between q and p： $$ \mathbf{||q-p||} $$

A unit vector：

$$ \mathbf{||p||} =1 $$

Normalization： $$ \mathbf{\bar{p} =p/||p||} $$

P10

Vector Arithematic: Dot Product

A dot product, also called inner product, is:

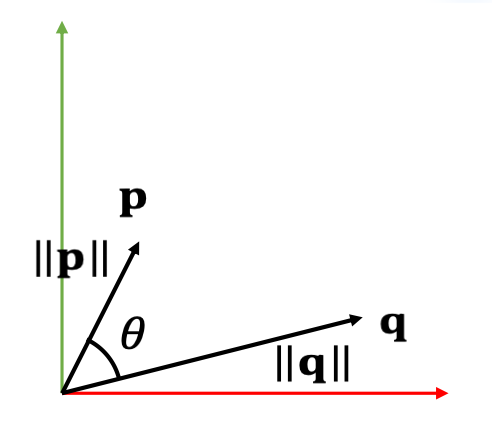
Geometric Meanings

$$ \begin{array}{c} \mathbf{p\cdot q}=p_xq_x+p_yq_y+p_zq_z=\mathbf{p^Tq} \\ =||\mathbf{p} ||||\mathbf{q} ||\cos \theta \end{array} $$

$\mathbf{p\cdot q=q\cdot p} $
$\mathbf{p\cdot (q+r)=p\cdot q+p\cdot r} $
$\mathbf{p \cdot p = ||p||^2_2} $, a different way to write norm.
If $\mathbf{p·q} = 0$ and $\mathbf{p,q}\ne 0$ then $\cos \theta = 0$,then $\mathbf{p}$ and $\mathbf{q}$ are orthogonal.

P11

Example 2: Particle-Line Projection

✅$X$为物体中心点的位置，为物体上所有点的整体位移，是前面说的$T$.
速度是加速度的积分，表示为$V$或$\dot{X} $
加速度为$F／M$，但$F$比较复杂，与时间、位置、速度都可能有关系。
位置是速度的积分。

P12

Example 3: Plane Representation

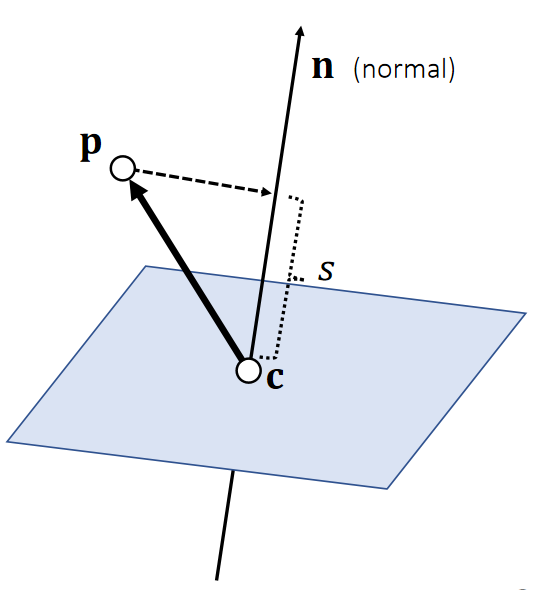
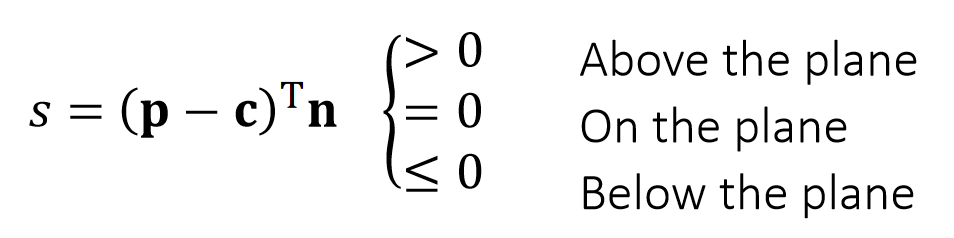
S: The signed distance to the plane

Quiz: How to test if a point is within a box?

P13

Example 4: Particle-Sphere Collision

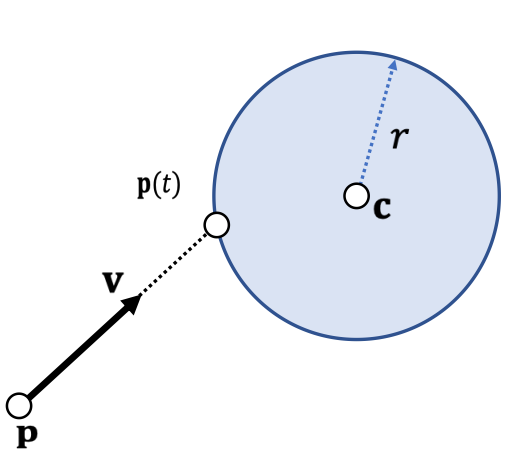
If collision does happen, then:

$$ ||\mathbf p(t) - \mathbf{c}||^2= r^2 $$

$$ (\mathbf p-\mathbf c+t\mathbf v)·(\mathbf p-\mathbf c +t\mathbf v) =r^2 $$

$$ (\mathbf v·\mathbf v)t^2+2(\mathbf p-\mathbf c)·\mathbf vt+ (\mathbf p-\mathbf c)·(\mathbf p-\mathbf c)-r^2=0 $$

Three possiblities:
- No root、无碰撞
- One root、擦边 if $t > 0$
- Two roots:自碰撞 if $t > 0 $

P14

Vector Arithematic: Cross Product

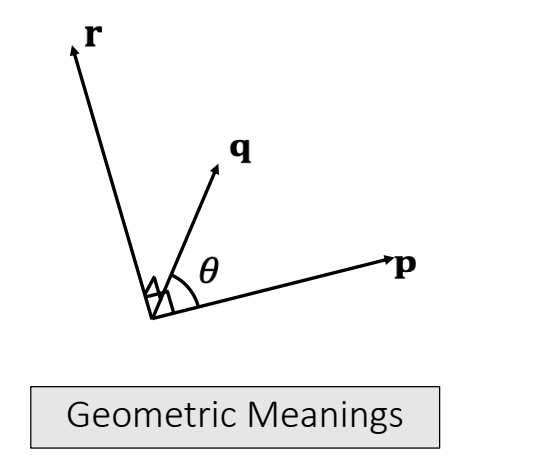
The result of a cross product is a vector:

$$ \mathbf{r=p\times q} =\begin{bmatrix} p_yq_z-p_zq_y \\ p_zq_x-p_xq_z\\ p_xq_y-p_yq_x\\ \end{bmatrix} $$

$\mathbf r·\mathbf p = 0; \mathbf r·\mathbf q = 0; ||\mathbf r|| = ||\mathbf p||||\mathbf q|| \sin \theta$
$\mathbf p\times \mathbf q =-\mathbf q\times \mathbf p$
$\mathbf p\times (\mathbf q +\mathbf r) = \mathbf p\times \mathbf q +\mathbf p\times \mathbf r$
If $ \mathbf p \times \mathbf q =\mathbf 0$ and $\mathbf p,\mathbf q\ne 0 $ then $\sin \theta= 0$, then $\mathbf p$ and $\mathbf q $ are parallel (in the same or opposite direction).

P15

Example 5: Triangle Normal and Area

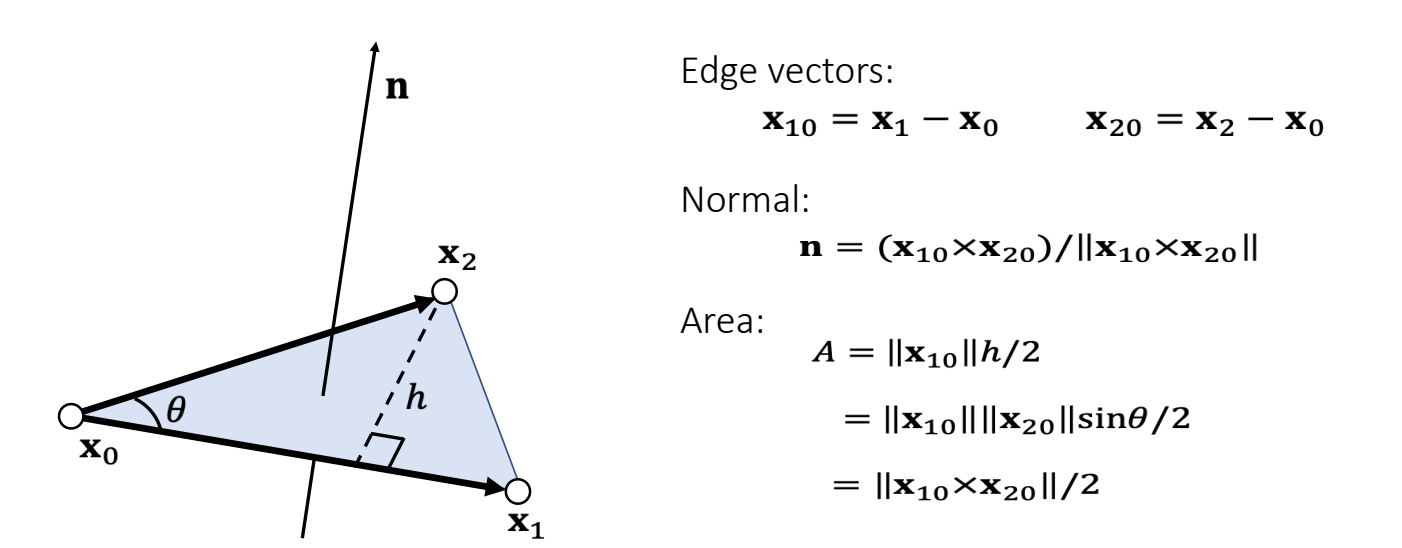
Cross product gives both the normal and the area.
The normal depends on the triangle index order, also known as topological order.

P16
Quiz: How to test if three points are on the same line (co-linear)?

P17

Example 6: Triangle Inside/Outside Test

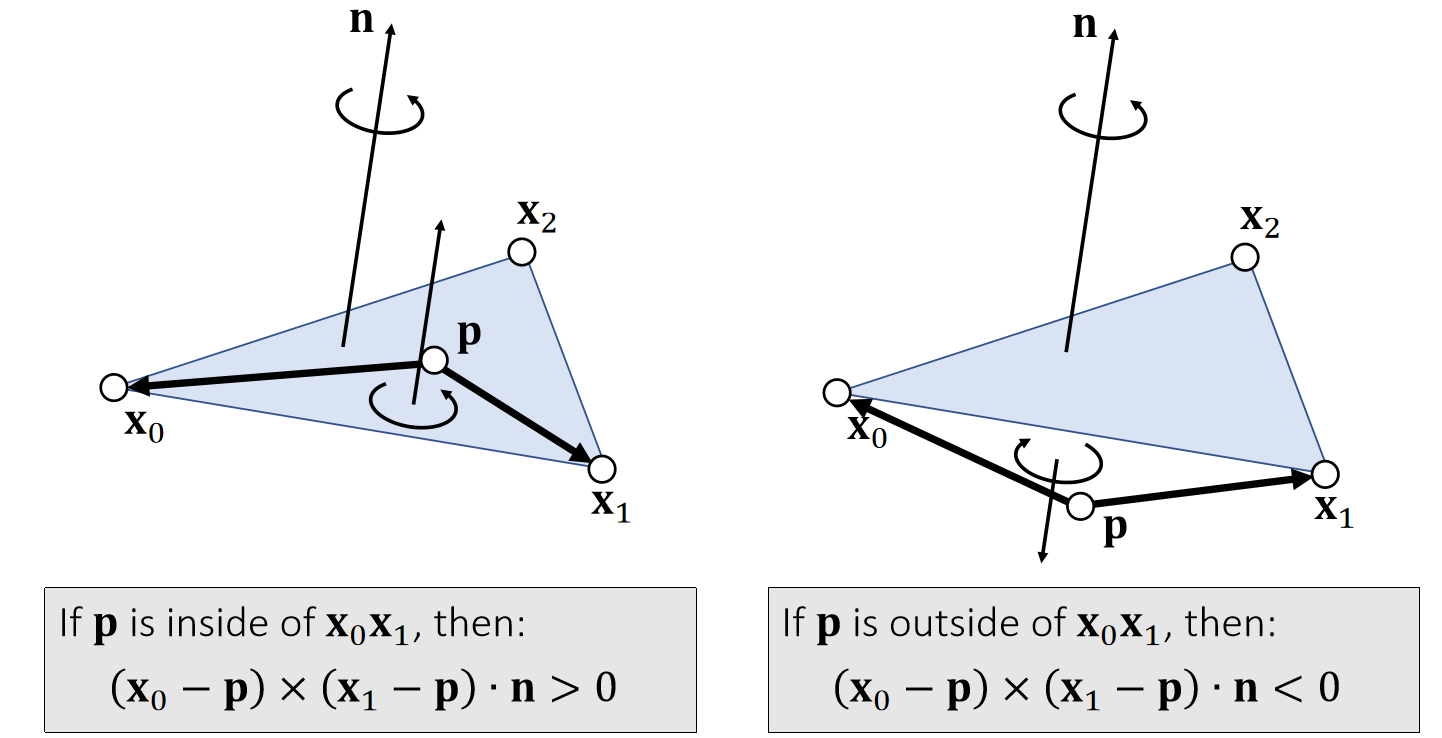
P18

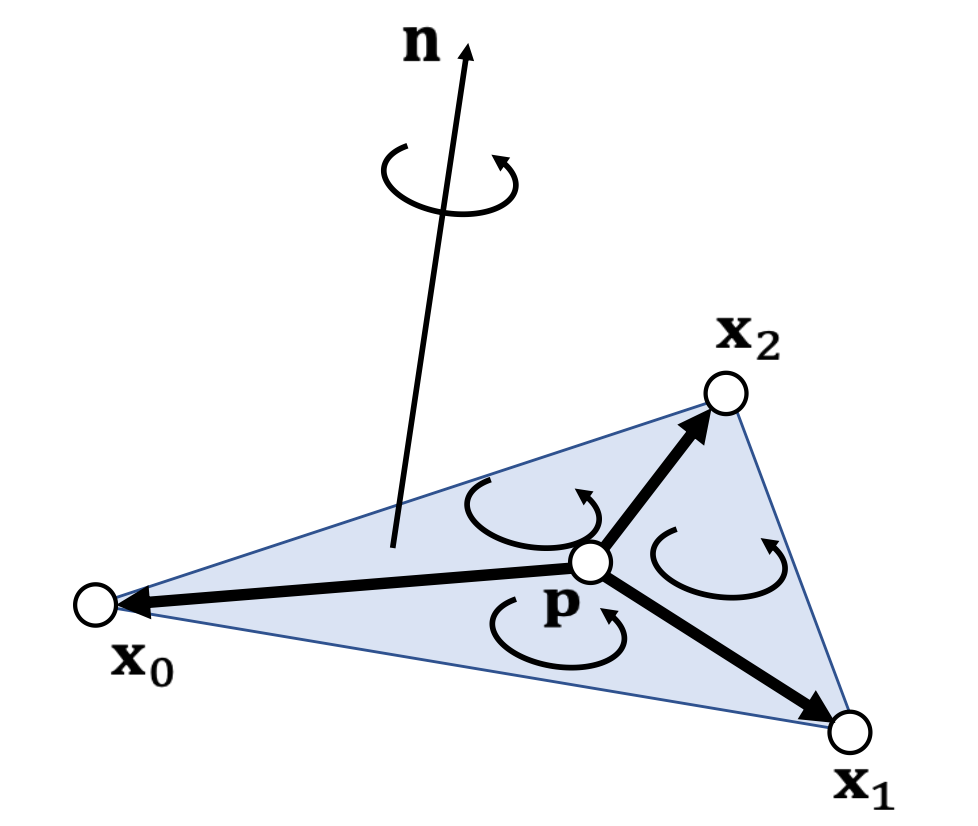
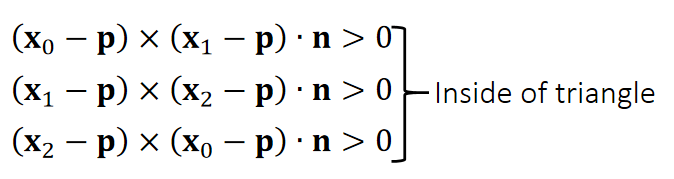
Otherwise, outside.

✅ 假设P点在三角形所在平面上
三个点的顺序很重要，不能搞反。

P19

Example 7: Barycentric Coordinates

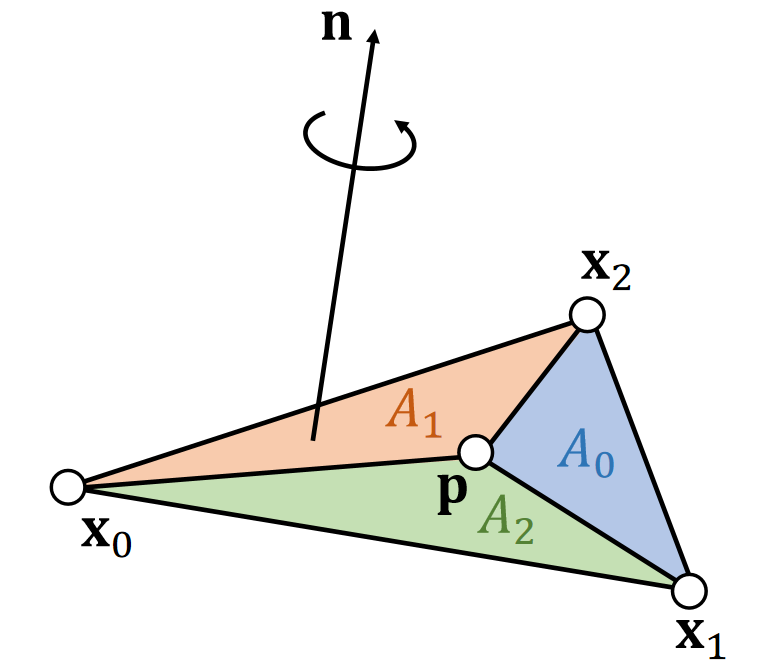
Note that:

$$ \frac{1}{2} \mathbf{(x_0−p)×(x_1−p)\cdot n} =\begin{cases} \frac{1}{2}||\mathbf{(x_0−p)×(x_1−p)} ||& \mathrm{inside} \\
\frac{1}{2}||\mathbf{(x_0−p)×(x_1−p)} || & \mathrm{outside} \end{cases} $$

Signed areas:

$$ \mathbf{A_2=\frac{1}{2} (x_0−p)×(x_1−p)\cdot n} $$

$$ \mathbf{A_0=\frac{1}{2} (x_1−p)×(x_2−p)\cdot n} $$

$$ \mathbf{A_1=\frac{1}{2} (x_2−p)×(x_0−p)\cdot n} $$

$$ \mathbf{A_0+A_1+A_2=A} $$

Barycentric weights of p :

$$ b_0=A_0/A \quad b_1=A_1/A \quad b_2=A_2/A $$

$$ b_0+b_1+b_2=1 $$

Barycentric Interpolation

$$ \mathbf{p} =b_0\mathbf{x} _0+b_1\mathbf{x} _1+b_2\mathbf{x} _2 $$

✅ 当 $\mathbf{p}$ 在三角形外面时，面积为负，但面积总和不变 $b_0,b_1,b_2$ 为 $\mathbf{p}$ 在三角形重心坐标系下的坐标

✅ $\mathbf{p}$ 在三角形外部、重心坐标同样适用，不过权重有负数。

P20

Gouraud Shading

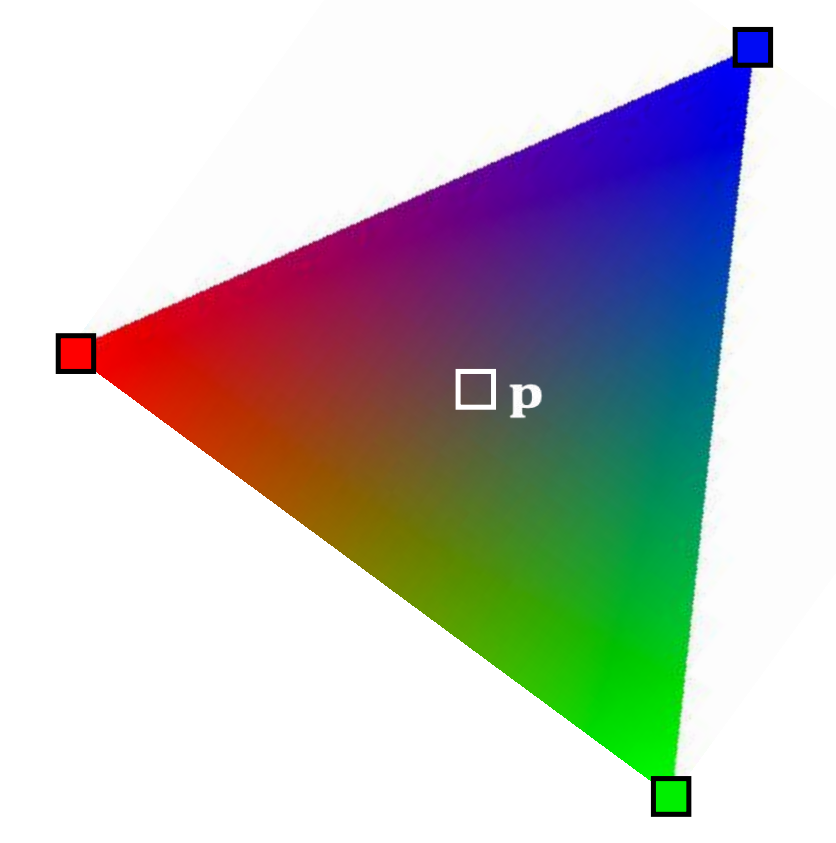
Barycentric weights allows the interior points of a triangle to be interpolated.
In a traditional graphics pipeline, pixel colors are calculated at triangle vertices first, and then interpolated within. This is known as Gouraud shading.
It is hardware accelerated.
It is no longer popular.

✅ 由于硬件能力提升，已经可以做到逐像素。
shading,不再需要此方法
通常也不是逐像素计算重心坐标，而是扫描线算法
例如要计算某一行，可以：
(1) 插值出行起点像素；
(2) 插值出行终点像素；
(3) 起点与终点间批量插值；

P21

Example 9: Tetrahedral Volume

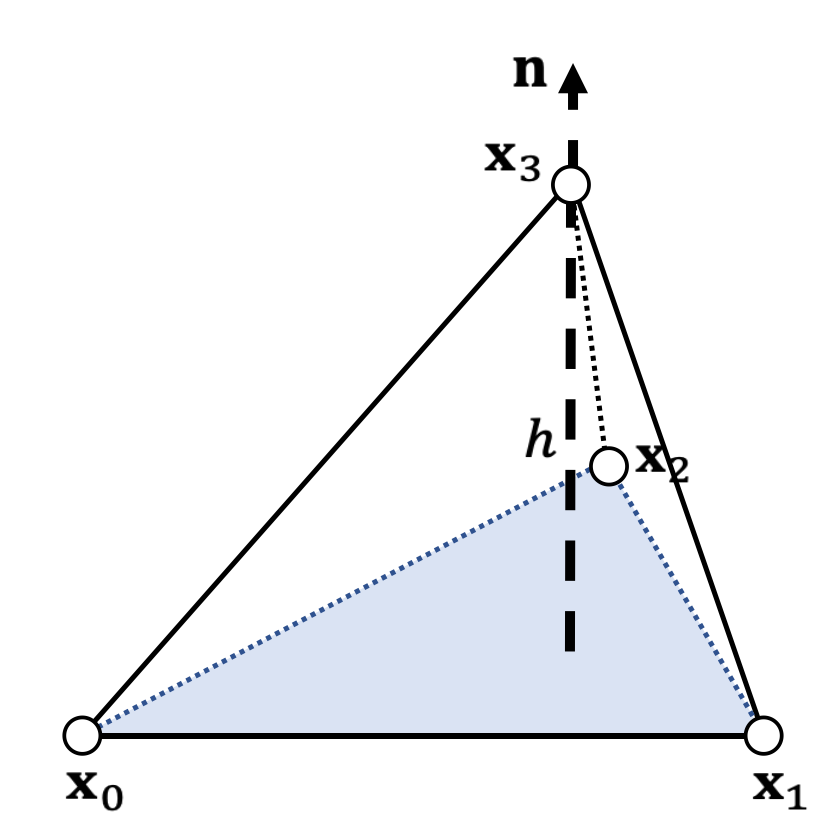
Edge vectors:

$$ \mathbf{X_{10}=X_1-X_0 \quad \quad X_{20}=X_2-X_0 \quad \quad X_{30}=X_3-X_0} $$

Base triangle area:

$$ A=\frac{1}{2} ||\mathbf{X} _{10}\times \mathbf{X} _{20}|| $$

Height:
$$ h=\mathbf{x} _{30}\cdot\mathbf{n} =\mathbf{x} _{30}\cdot \frac{\mathbf{x} _{10}\times \mathbf{x} _{20}}{||\mathbf{x} _{10}\times \mathbf{x} _{20}||} $$

Volume:

$$ \begin{align*} V&=\frac{1}{3} ℎA=\frac{1}{6} \mathbf{x} _{30}\cdot \mathbf{x} _{10}\times \mathbf{x} _{20}\\ &=\frac{1}{6}\begin{vmatrix} \mathbf{x} _1 & \mathbf{x} _2 & \mathbf{x} _3 &\mathbf{x} _0 \\ 1& 1 & 1 &1 \end{vmatrix} \end{align*} $$

✅ 四面体
$h$是$\mathbf{x}_{30}$在 normal 上的投影
行列式是上面叉乘的另一种马法。

P22

Note that the volume $V =\frac{1}{3}h\mathit{A} =\frac{1}{6} \mathbf{x} _ {30}\cdot (\mathbf{x} _ {10}\times \mathbf{x}_{20})$ is signed.

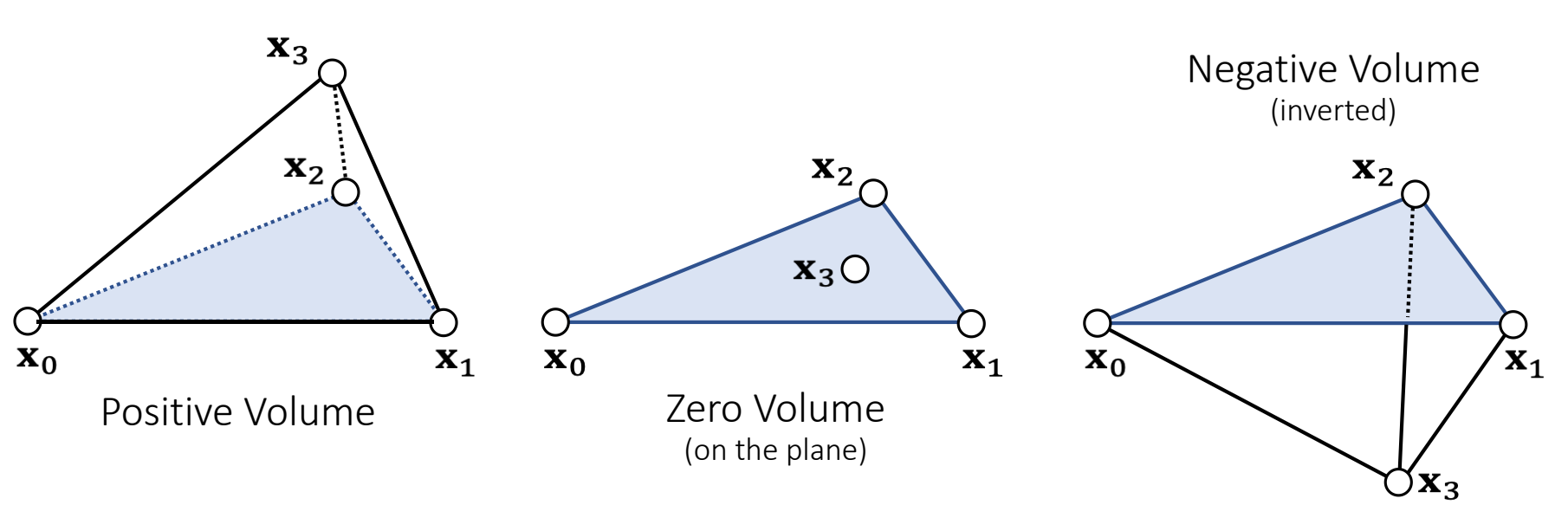
✅ $\mathbf{x}_{3}$的后面法线的同方向上，也正四面体，反之为负四面体，四点共面为零体积。

P23

Example 10: Barycentric Weights (cont.)

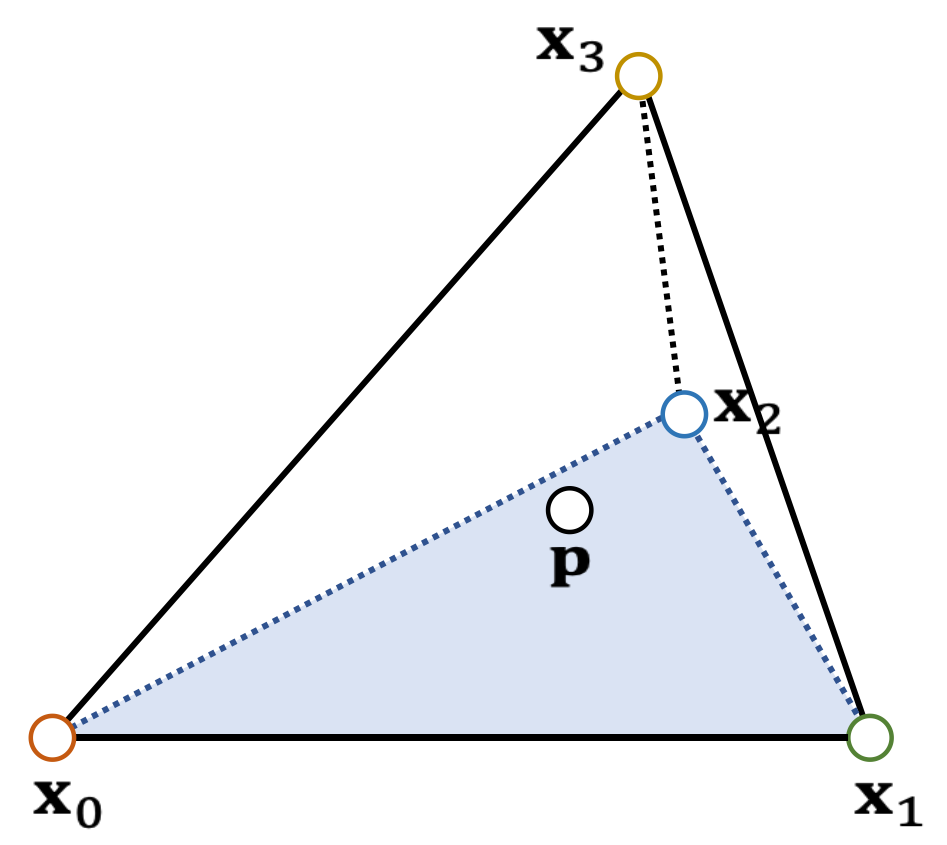
p splits the tetrahedron into four sub-tetrahedra:

$$ \begin{matrix} V_0=\mathrm{Vol} (\mathbf{x}_3,\mathbf{x}_2, \mathbf{x}_1, \mathbf{p} )\\ V_1=\mathrm{Vol} (\mathbf{x}_2,\mathbf{x}_3, \mathbf{x}_0, \mathbf{p} )\\ V_2=\mathrm{Vol} (\mathbf{x}_1,\mathbf{x}_0, \mathbf{x}_3, \mathbf{p} )\\ V_3=\mathrm{Vol} (\mathbf{x}_0,\mathbf{x}_1, \mathbf{x}_2, \mathbf{p} ) \end{matrix} $$

p is inside if and only if: $V_0,V_1,V_2, V_3 > 0$.
Barycentric weights:
$$ b_0=V_0/V \quad b_1=V_1/V \quad b_2=V_2/V \quad b_3=V_3/V $$

$$ b_0+b_1+b_2+b_3=1 $$

$$ \mathbf{p} =b_0\mathbf{x} _0+b_1\mathbf{x} _1+b_2\mathbf{x} _2+b_3\mathbf{x} _3 $$

P24

Example 11: Particle-triangle Intersection

First, we find t when the particle hits the plane:

$$ (\mathbf{p} (t)−\mathbf{x} _0)\cdot \mathbf{x} _{10}\times \mathbf{x} _{20}=0 $$

$$ (\mathbf{p}-\mathbf{x} _0+t\mathbf{v})\cdot \mathbf{x} _{10}\times \mathbf{x} _{20}=0 $$

$$ t=\frac{(\mathbf{p}−\mathbf{x}_0)\cdot \mathbf{x} _{10}\times \mathbf{x} _{20}}{\mathbf{v}\cdot \mathbf{x} _{10}\times \mathbf{x} _{20}} $$

We then check if $\mathbf{p}(t)$ is inside or not.
- See Example 6.

✅ 代入体积公式，体积为0时发生碰撞

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/