力与力矩

力矩 torque $\mathbf{τ} $

Torque：力矩，造成物体旋转的趋势。类比于Force：力，造成物体运动的趋势。

力转化为力矩

✅ 力转化为力矩，不是物理性质上的转化，而是数学形式上的转化。把力用力矩的形式表达，用于计算它对旋转产生的影响。

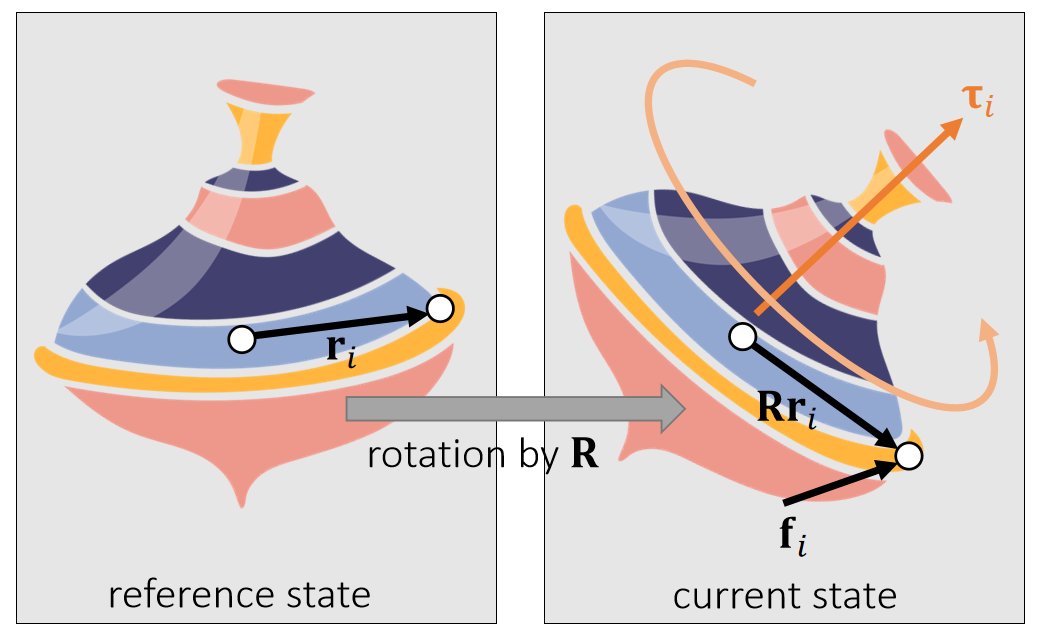
定义：

(\mathbf{f} _i\)：力
$\mathbf{Rr} _i$：当前状态下质心到作用点的向量
$\mathbf{τ} _i$：力矩

分析：

$\mathbf{τ} _i$ is perpendicular to both vectors: $\mathbf{Rr} _i$ and $\mathbf{f} _i$.
$\mathbf{τ} _i$ is porportional to ||$\mathbf{Rr} _i$|| and ||$\mathbf{f} _i$||.

✅ 力矩的大小决定旋转的快慢。

$\mathbf{τ} _i$ is porportional to $\sin \theta$.

✅ $\theta$ is the angle between (\mathbf{f} _i\)和$\mathbf{Rr} _i$

因此：

$$ \mathbf{τ} _i\longleftarrow (\mathbf{Rr} _i)\times \mathbf{f} _i $$

inertia tensor

inertia 看作是对运动的抵抗。

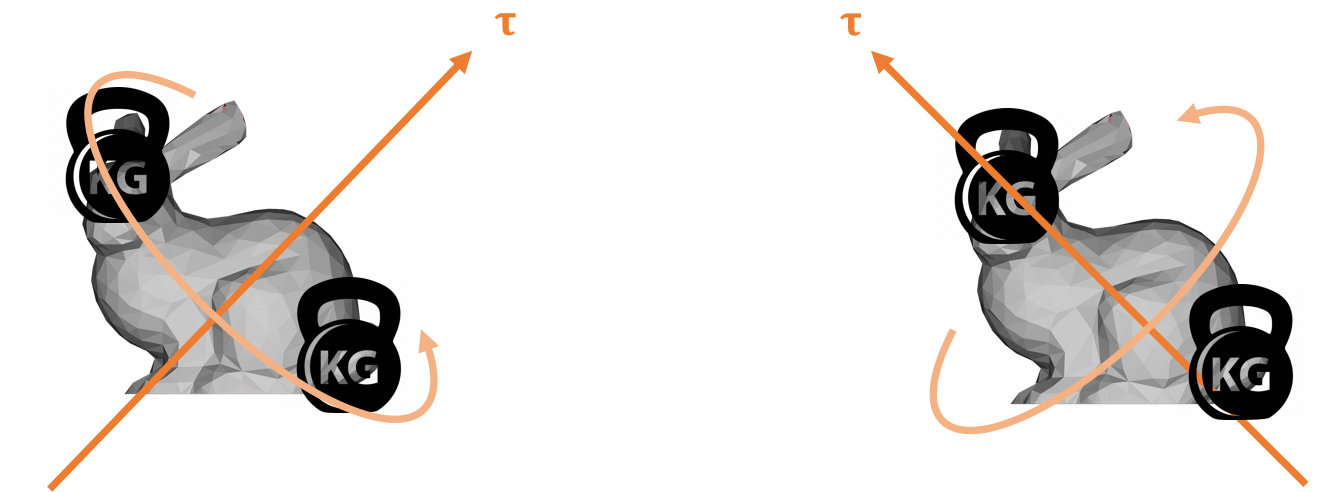
Which side receives greater resistance?

✅ 两图对同一个刚体施加的力矩大小相同，但产生的旋转不同。可知inertia的效果与力矩的方向有关，因此不是常数。

换个角度出，对两个不同（旋转）状态的刚体施加（大小和方向）相同的力矩，其产生的效果也不一样。

即，inertia 与自身的状态相关。

计算inertia

Similar to mass, an inertia tensor describes the resistance to rotational tendency caused by torque. But different from mass, it’s not a constant.

It’s a matrix! The mass inverse is the resistance (just like mass).

✅ 用于旋转的质量不再是实数，而是$3\times 3$的矩阵，称为 Inertia 矩阵。
✅ 用 $\mathbf{I}$ 来标记当前状态下的 Inertia 矩阵。用 $\mathbf{I}_{ref}$为参考状态下的Inertia 矩阵。

具体计算公式如下：

reference state	current state

\(\mathbf{I} _{\mathbf{ref} }=\sum m_i(\mathbf{r} _i^\mathbf{T} \mathbf{r} _i\mathbf{1} −\mathbf{r} _i\mathbf{r} _i^\mathbf{T} )\) \(\mathbf{1}\) is the 3-by-3 identity.	\(\mathbf{I} =\sum m_i(\mathbf{r} _i^\mathbf{T}\mathbf{R} ^\mathbf{T}\mathbf{Rr} _i\mathbf{1} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )\) \(\quad=\sum m_i(\mathbf{Rr} _i^\mathbf{T}\mathbf{r} _i\mathbf{1R} ^\mathbf{T} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )\) \(\quad=\sum m_i\mathbf{R}(\mathbf{r}_i^\mathbf{T}\mathbf{r}_i\mathbf{1}−\mathbf{r}_i\mathbf{r}_i^\mathbf{T} ) \mathbf{R^T}\) \(\quad=\mathbf{RI _{ref}R^T}\)

reference state

current state

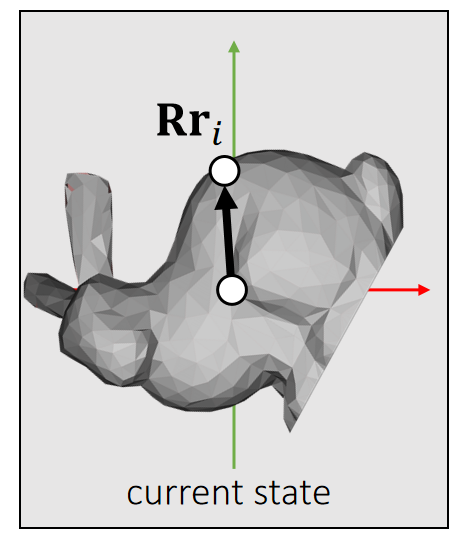$\mathbf{I} _{\mathbf{ref} }=\sum m_i(\mathbf{r} _i^\mathbf{T} \mathbf{r} _i\mathbf{1} −\mathbf{r} _i\mathbf{r} _i^\mathbf{T} )$
$\mathbf{1}$ is the 3-by-3 identity.

$\mathbf{I} =\sum m_i(\mathbf{r} _i^\mathbf{T}\mathbf{R} ^\mathbf{T}\mathbf{Rr} _i\mathbf{1} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$
$\quad=\sum m_i(\mathbf{Rr} _i^\mathbf{T}\mathbf{r} _i\mathbf{1R} ^\mathbf{T} −\mathbf{Rr} _i\mathbf{r} _i^\mathbf{T} \mathbf{R^T} )$
$\quad=\sum m_i\mathbf{R}(\mathbf{r}_i^\mathbf{T}\mathbf{r}_i\mathbf{1}−\mathbf{r}_i\mathbf{r}_i^\mathbf{T} ) \mathbf{R^T}$
$\quad=\mathbf{RI _{ref}R^T}$

✅ 不需要每次都根据当前状态计算，而是基于一个已经算好的ref状态的 inertia快速得出。

P33

After-Class Reading (Before Collision)

P35

https://graphics.pixar.com/pbm2001

✅ 建议读其中的Rigid Body Dynamics部分

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/

GAMES103

力与力矩

力矩 torque \(\mathbf{τ} \)

力转化为力矩

inertia tensor

计算inertia

After-Class Reading (Before Collision)