MPM

物质点法 (material point method, MPM)采用拉格朗日和欧拉双重描述，将物体离散为一组在空间网格中运动的质点。

• 质点携带了所有的物质信息，如质量、速度、应变和应力等，可很方便地跟踪材料的界面和引入与变形历史相关的材料模型。
• 质点在空间网格中运动，运动方程在空间网格上求解，避免了网格畸变问题，适合于分析特大变形及流动问题。

核心思想

拉格朗日视角 (粒子)：物质点携带密度、速度、应力等信息，随物质变形运动。
欧拉视角 (背景网格)：划分计算域，用于计算空间导数和物理量更新。
粒子-网格-粒子 (P-G-P)：信息通过物质点映射到网格节点，在网格上计算更新，再插值回物质点，完成一个时间步。

主要特点与优势

融合拉格朗日与欧拉：兼具拉格朗日法的精确追踪物质界面能力和欧拉法的网格独立性，避免了有限元网格缠绕畸变问题。
处理大变形：能有效模拟材料的超大变形、破碎、断裂等非线性问题。
自动处理多体接触：物质点在网格内运动，自动处理多介质界面，无需复杂的碰撞检测。
适用范围广：适用于高速碰撞、爆炸冲击、岩土动力学、流体与固体相互作用等复杂问题。

但 MPM 在精度上存在劣势。

基本步骤（一个时间步）

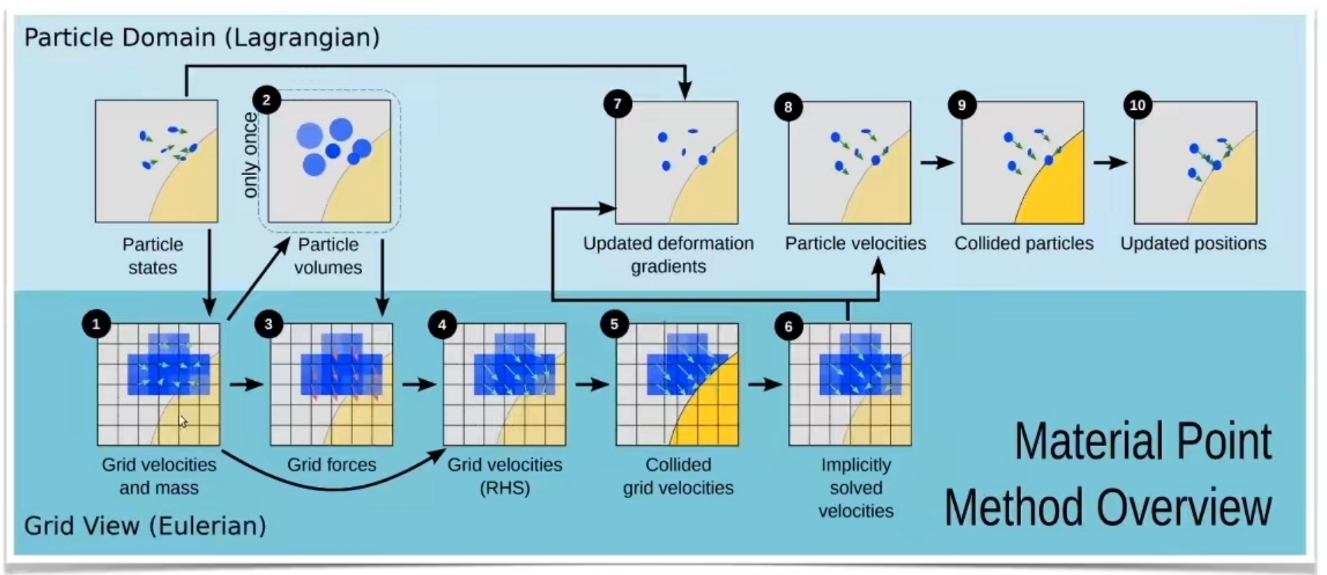
粒子到网格 (P2G)：将物质点信息（如质量、动量）通过插值函数映射到背景网格节点。
网格计算：在背景网格上，根据控制方程（如动量守恒）计算节点力、加速度等。
网格到粒子 (G2P)：将网格上的计算结果（如速度、应力）通过插值函数传回物质点。
更新粒子：更新物质点的位置、速度和应力状态。
（可选）丢弃网格：根据需要重新划分或更新背景网格。

🔎 Deborah Sulsky, Shi-Jian Zhou, and Howard L Schreyer. Application of a particle-in-cell method to solid mechanics.

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/