三维弹性力学
变形梯度 deformation gradient
将未变形的弹性体置于坐标系中,用 Ω 表示弹性体占据的体积域,该区域被称为参考构形(或未变形构形)。
用大写字母表示的向量X∈Ω指代未变形构形中的单个物质点。
弹性体发生变形时,每个物质点X都会位移至新的变形位置,该位置用小写字母表示的向量x指代。
物质点与其变形后位置的对应关系由变形函数ϕ:R3→R3描述,该函数将每个物质点X映射至其变形后的位置x=ϕ(X)。
变形梯度张量F∈R3×3是变形映射的雅可比矩阵。
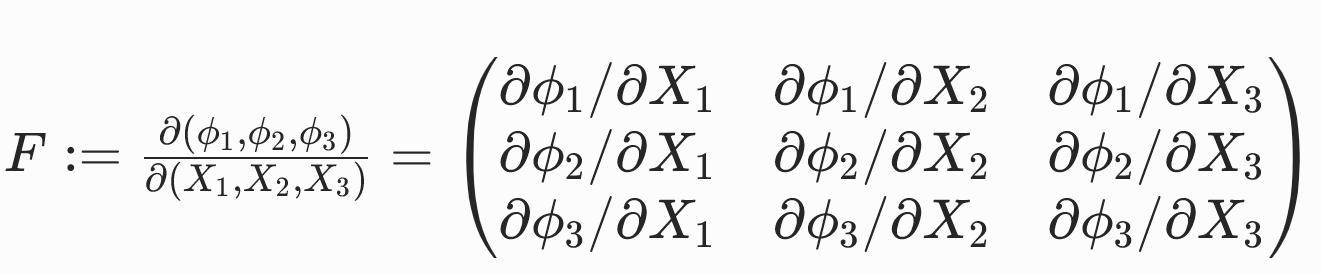
变形函数与变形梯度举例:
| 形变 | 变形函数ϕ | 变形梯度F |
|---|---|---|
| 平移 | x =ϕ( X )= X + t | F=∂ϕ( X )/∂ X =I |
| 均匀缩放 | ϕ( X )=γ X | F=γI |
| 各向异性缩放 | ϕ( X )=S X | F=S |
| 旋转 | ϕ( X )=RX | F=R |
应变能与超弹性
弹性变形会积累势能,该势能被称为应变能,用E[ϕ]表示。
应变能仅与最终的变形形态有关,而与弹性体达到该构形的时间变形路径无关。这是超弹性材料的标志性特征。
弹性体不同部位的变形程度存在差异,因此,变形与应变能的关系更适合在局部尺度上定义。因此引入能量密度函数Ψ[ϕ;X]。
Ψ[ϕ;X]用于度量物质点X周围微元域dV内,单位未变形体积的应变能。
对能量密度函数在整个体积域 Ω 上积分,即可得到弹性体的总应变能:
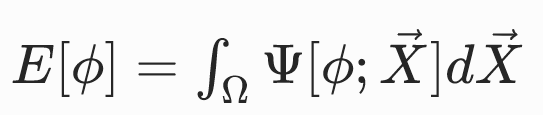
由于能量密度Ψ[ϕ;X]定义在X的局部域上,因此可通过一阶泰勒展开对该微小区域的变形映射进行合理近似:
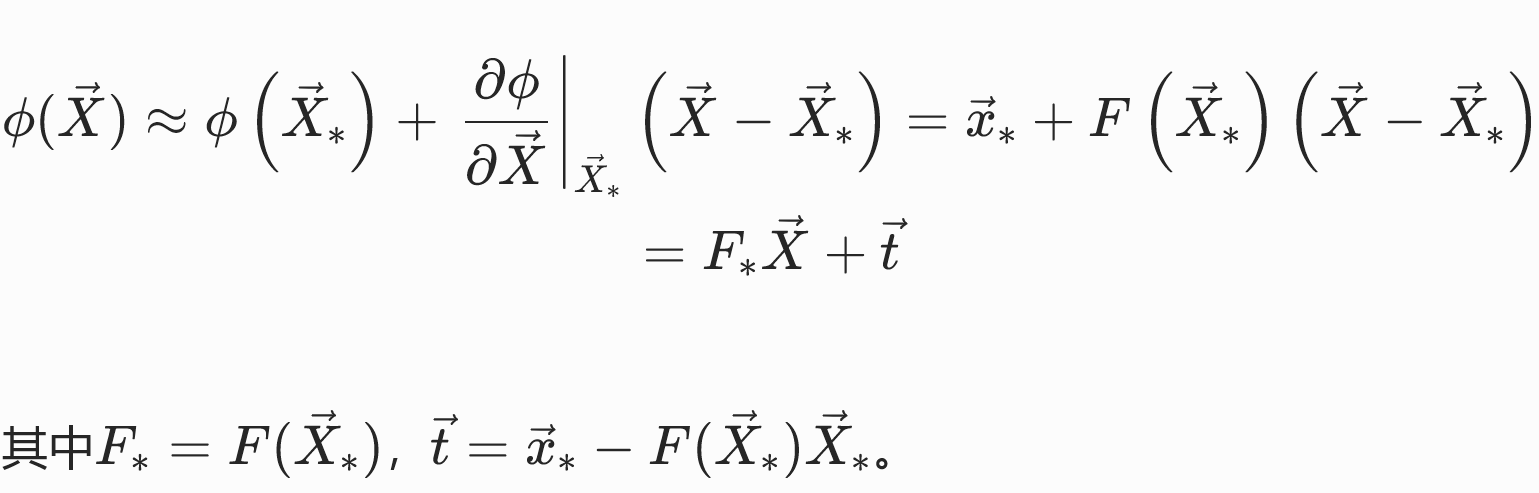
其中t对能量不影响,因此能量密度仅为局部变形梯度的函数。但Ψ(F)的具体形式与材料特性有关。
能量密度函数一个自然的期望性质是下有界,即存在最小能量状态,弹性体可稳定于该状态。
能量密度函数举例:
| 能量密度函数 | 稳定状态 | 特点 |
|---|---|---|
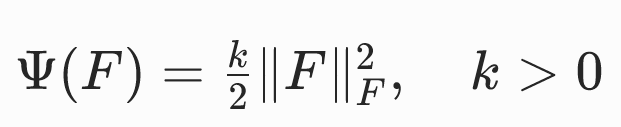 | F=0,ϕ(X)=常数 | 所有物质点都有收缩至同一点的趋势。 不符合自然规律,因为参考构形 Ω 并非其平衡构形。 |
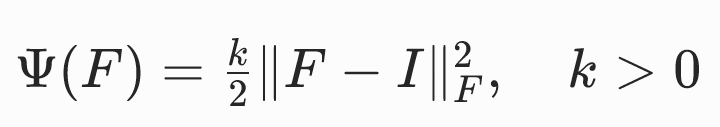 | F=I,ϕ(X)=X) | 处于参考构形或其恒定平移构形时,能量取得最小值。但旋转状态下的能量非零。 |
力(Force)与面力(Traction)
力密度,为物质点X周围微元域内,单位未变形体积的力。
对应的:面力密度函数traction(X),用于度量弹性体边界上物质点X周围微元域内,单位未变形面积的力。
对有限边界区域B⊂∂Ω积分,即可得到该边界区域的总作用力:
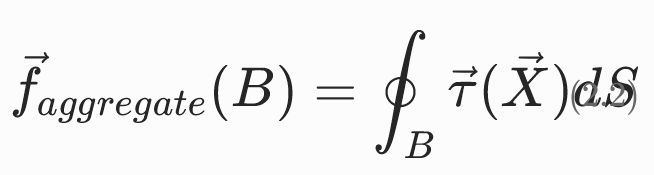
应力张量
The First Piola-Kirchhoff 应力张量
定义:
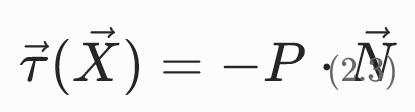
其中N为参考构形(未变形)中边界的单位外法向量。
对于超弹性材料,P仅为变形梯度的函数,且与应变能存在简单的关系:
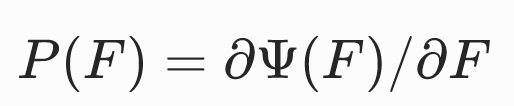
因此任意给出Ψ(F)或者P(F)中的一个,即可根据F得出traction τ ( X )
应力张量使用举例
定义:
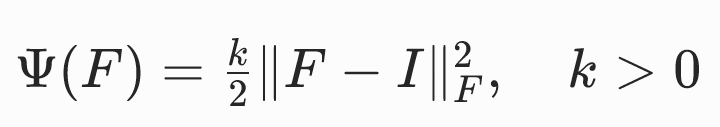
可以推导出:P=∂Ψ/∂F=k(F−I)
考虑弹性体沿所有方向均匀拉伸 2 倍的情况,ϕ( X )=2 X时,F=2I,P=kI,τ =−k N,该边界力会使弹性体产生向内的运动,以恢复原始的形状和体积。
材料本构模型
对材料物理特性的数学描述被称为本构模型,其中包含将外界激励(如变形)与材料响应(如力、应力、能量)关联起来的方程。
基于F的本构方程
将Ψ与F(或P与F)关联的显式公式完全可作为本构方程,例如:
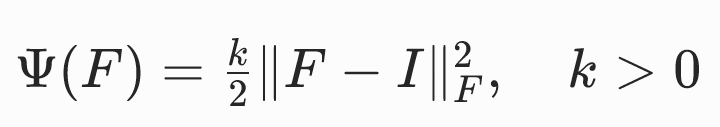
但直接利用矩阵F的元素分析变形的类型和程度非常不直观,通常会定义一些由F推导得到的中间量来定义本构方程。
中间度量
应变度量(Strain measures)
应变度量是用于定量描述变形程度的物理量,即衡量当前构形与静息构形的偏离程度。
应变度量由变形梯度推F导得到,保留变形梯度中与变形程度评估相关的信息,同时舍弃变形梯度中与形状变化无关的信息。
格林应变张量
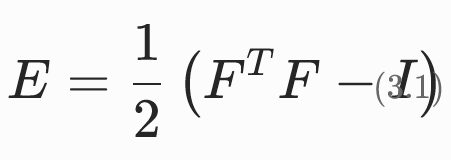
特点:
- 当弹性体处于参考构形(ϕ(X)=X)时,F=I,因此E=0;
- 当弹性体仅发生旋转和平移(形状不变)时,ϕ(X)=RX+t(R为旋转矩阵),此时F=R,由于RTR=I,因此E=0。
- 对于更一般的非刚体运动,可以将F分解为F=RS,此时
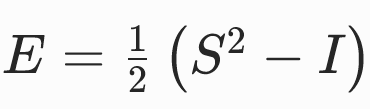
优点:
- 舍弃了与变形程度无关的旋转自由度,仅保留了对称因子S中包含的拉伸 / 剪切信息,且该过程无需显式进行极分解。
缺点:
- 格林应变张量是变形的非线性(二次)函数,因此基于格林应变张量构建的本构模型复杂度更高。
- 离散化后的节点力将是节点位置的非线性函数。
小应变张量
E(F)在E(I)处泰勒展开,并代入E(I)=0,得:
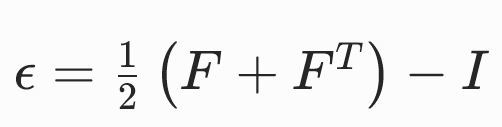
优点:
- 计算效率高
- 离散化后的节点弹性力与节点位置呈线性映射关系
缺点:
- 小应变张量仅能可靠地度量小变形。若用于大变形场景,将产生明显的误差。
共旋应变张量
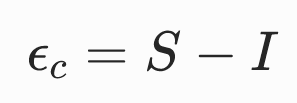
不变度量
各向同性不变量
$$ I_1(F) = tr (F^TF) $$
I1是F的各奇异值的平方和
体积比不变量J
$$ J = \det F $$
J的物理意义:变形引起的体积变化比。
本构模型
基于线性弹性(Linear elasticity)张量的本构模型

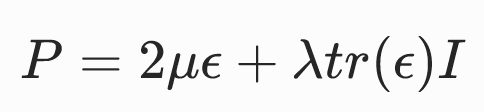
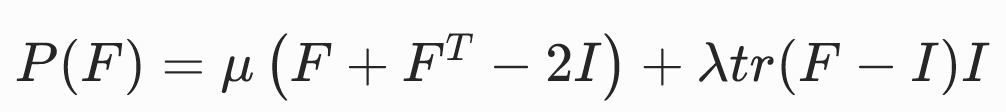
优点:
- 应力P是变形梯度F的线性函数,因此节点弹性力与节点位置呈线性关系。
- 与其他非线性材料模型相比,线弹性模型的计算成本显著更低。
- 在小变形场景下准确
缺点:
- 仅在小变形场景下准确,因此仅适用于运动幅度较小的情况。
基于格林应变张量的圣维南 - 基尔霍夫模型
将小应变模型中的ϵ(E的近似)替换为E
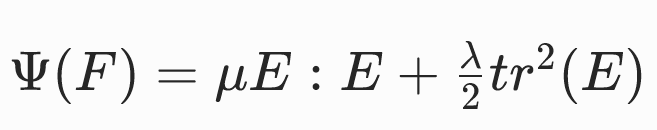
可求得
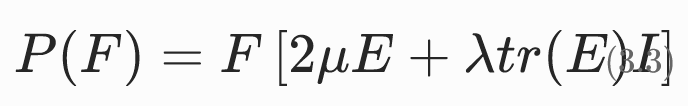
特点:
- 旋转不变性
- 非线性关系:应力是变形梯度F分量的三次多项式函数;离散化后,节点力也将表示为节点位置的三次多项式。
- 压缩缺陷:对强压缩的抵抗性较差。当弹性体受到强压缩力或运动学约束时,容易发生局部的扭曲和翻转。
基于共旋应变张量的共旋线性弹性模型
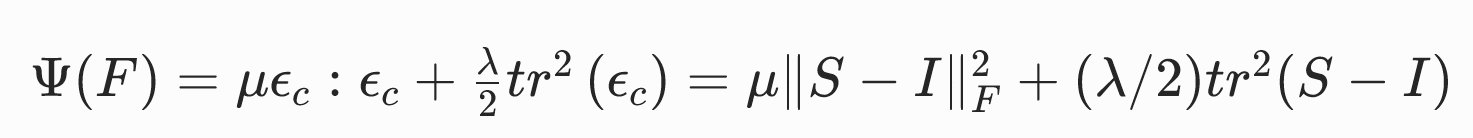
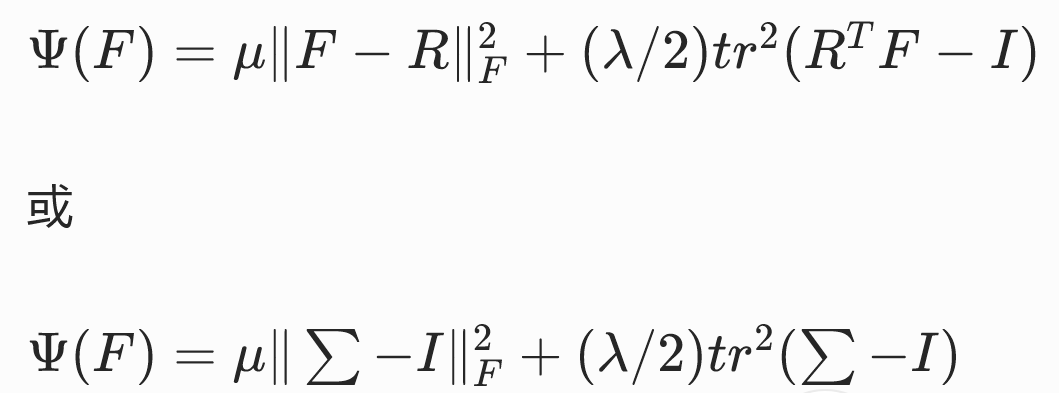
这三种写法的是等价的。
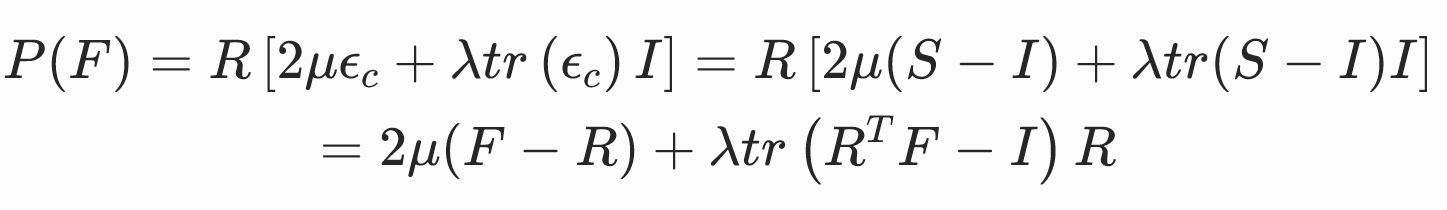
特点:
- 极分解的计算成本,以及在部分仿真中需要使用非线性求解器的成本。
- 相较于圣维南 - 基尔霍夫等高度非线性模型,其计算效率仍有显著优势。
新胡克弹性
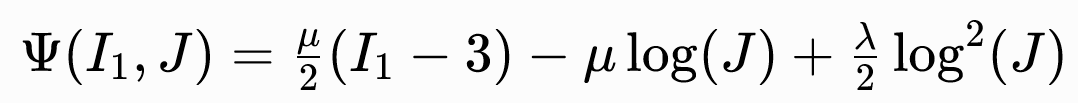
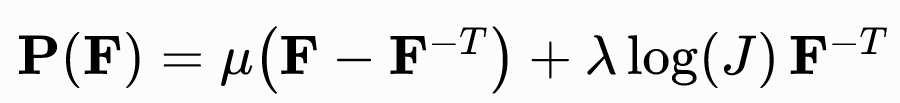
特点:
- 对极端压缩具有极强的抵抗效应。
- 近似不可压缩材料,实现保体积的数值格式。
- 当模拟中意外出现体积反转构型(理论上物理上不可能但实际仿真中极易发生)时,模型没有内置的稳定处理机制。
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/