粒子-网格法（Particle-in-Cell, PIC）

原理

• 原理：在流体模拟中结合粒子和网格，粒子携带速度等信息，网格用于求解压力泊松方程（实现不可压缩性）。

步骤：

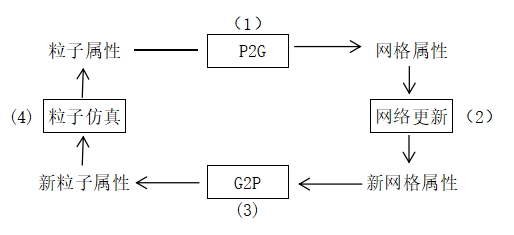
粒子到网格插值：

粒子属性与网格属性是分别用两种不同的载体来描述同一物理量。

将粒子的质量、电荷等属性分配到邻近网格节点。

分配时，距离近的点有更大的权重

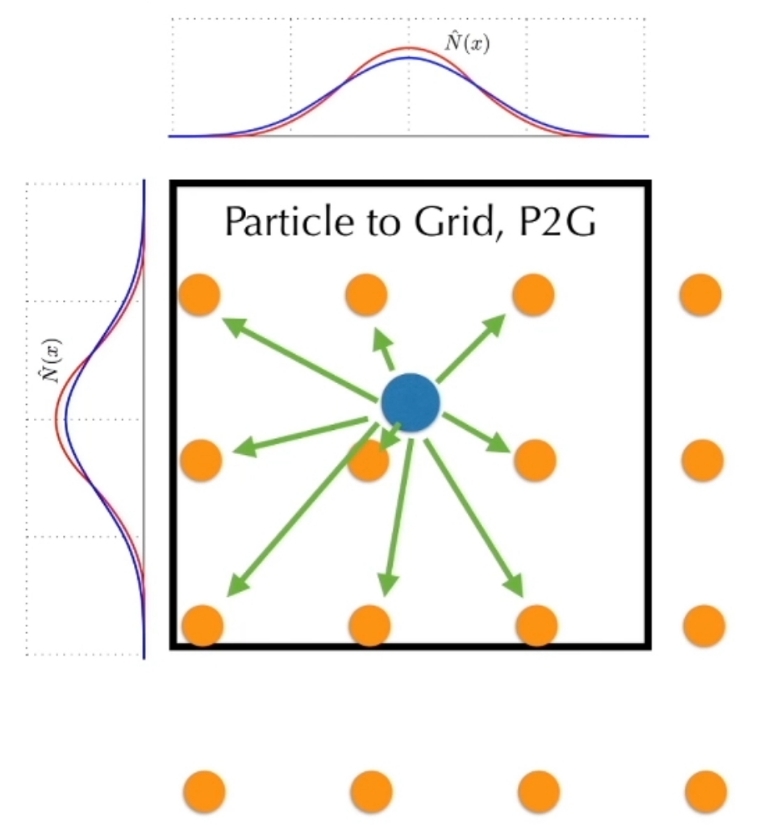
权重由核函和数定义

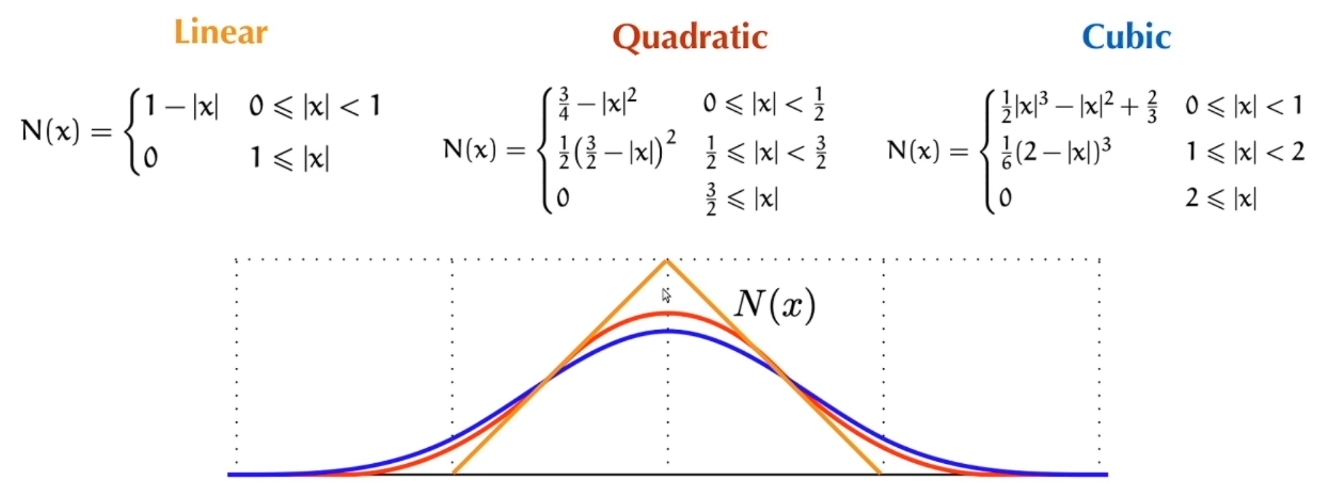
网格上求解场方程：

1. 施加外力
2. 在网格上求解泊松方程（静电场）或麦克斯韦方程（电磁场）等。 在 Grid 上解 presure，得到无散速度场
3. 处理边界

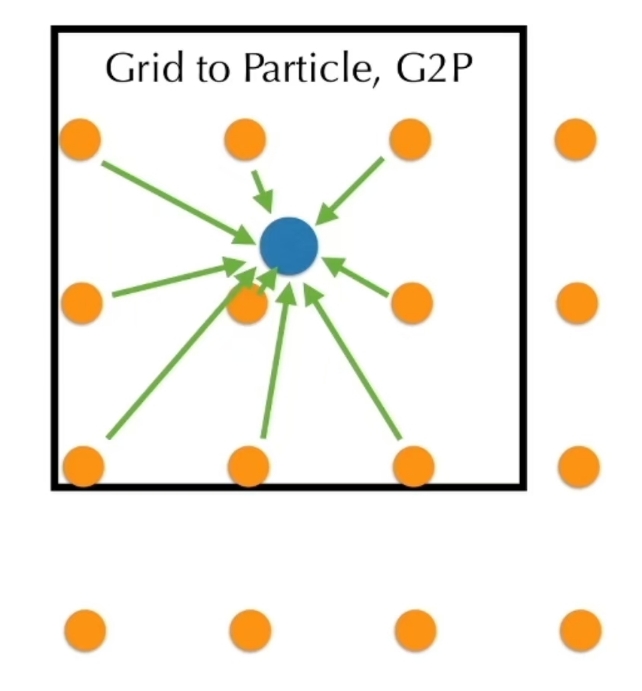
网格到场插值：

将网格节点上的场量(例如无散速度场)插值回粒子位置，更新粒子状态。

粒子推进：

根据牛顿定律更新粒子位置和速度。

可以是不同的积分法

应用：

等离子体模拟、天体物理（N体+网格）、流体模拟（如物质点法MPM）。

缺点：

能量耗散严重，表现为“黏”。
因为 G2P 过程有信息丢失

• Two solutions:
  1. Transfer more information: APIC, PolyPIC
  2. Transfer the delta: FLIP (later in this lecture)

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/