P19
Gradient Descent
Another way to solve \(\mathbf{x}^∗\)=argmin \(F(\mathbf{x})\) is the gradient descent method.
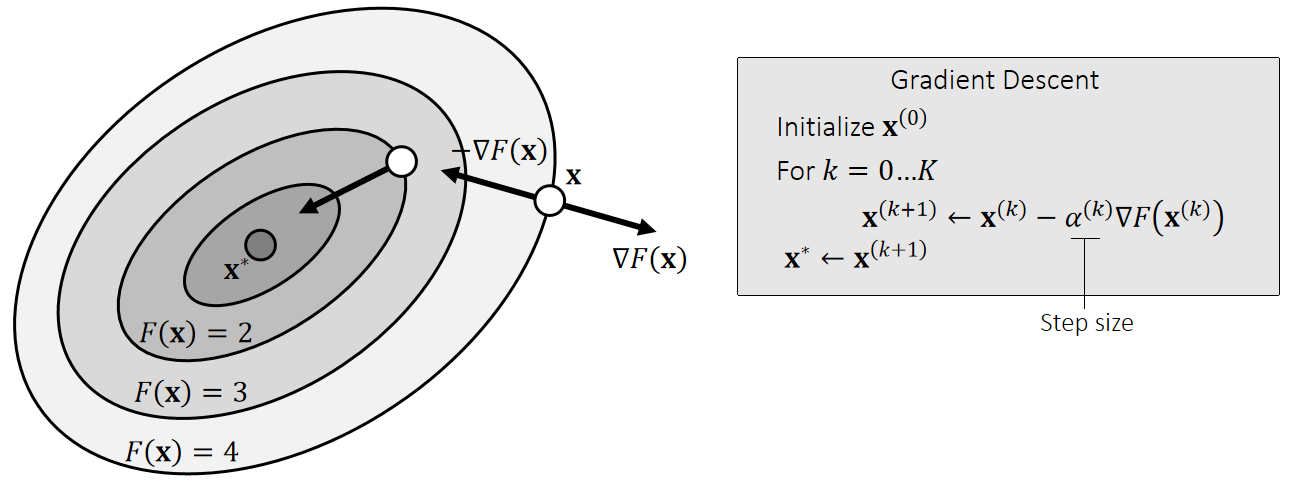
How to find the optimal step size becomes a critical question.
P20
step size adjustment
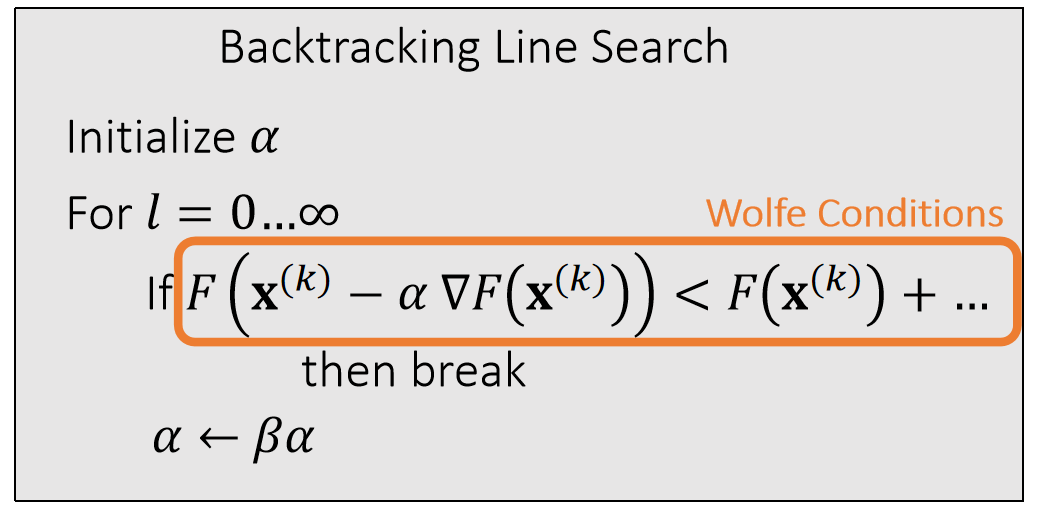
优点:simple, Low overhead
P21
Descent Directions
The direction \(\mathbf{d(x)}\) is descending, if a sufficiently small step size \(α\) exists for:
$$ F(\mathbf{x} )>F(\mathbf{x} +α\mathbf{d} (\mathbf{x} )) $$
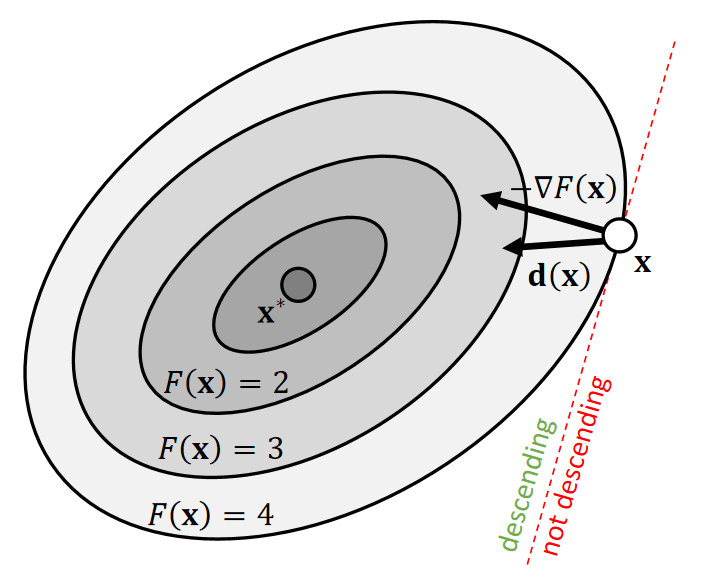
| In other words, \(−∇F(\mathbf{x} )\cdot \mathbf{d} (\mathbf{x} )>0\) |
|---|
✅沿负梯度方向可以下降,但不一定是最好的方向。怎样判断一个方向是否可以下降?答:看与负梯度方向是否在同侧。
P22
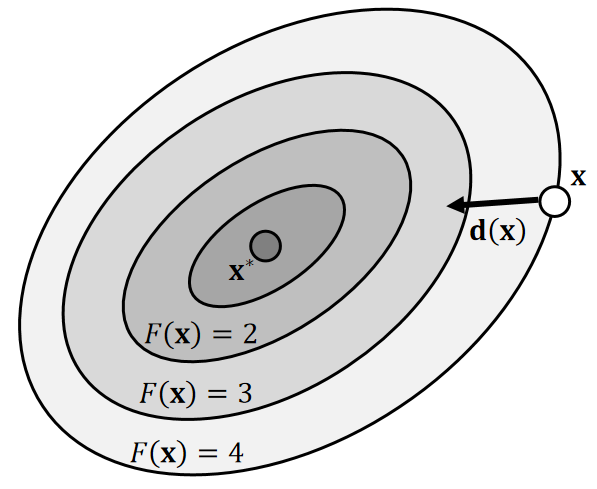
With line search, we can use any search direction as long as it’s descending:
$$ F(\mathbf{x} ^{(0)})>F(\mathbf{x} ^{(1)})>F(\mathbf{x} ^{(2)})>F(\mathbf{x} ^{(3)})>… $$
P23
Descent Methods
- Gradient descent is a descent method, since:
$$ \mathbf{d} (\mathbf{x} )=−∇F(\mathbf{x} )\quad \Rightarrow \quad −∇F(\mathbf{x} )\cdot (−∇F(\mathbf{x} ))>0 $$
- Newton’s method is also a descent method, if the Hessian is always positive definite:
$$ \mathbf{d} (\mathbf{x} )=−(\frac{∂^2F(\mathbf{x} )}{∂\mathbf{x} ^2})^{−1}∇F(\mathbf{x} ) \quad \Rightarrow \quad −∇F(\mathbf{x} )\cdot (−(\frac{∂^2F(\mathbf{x} )}{∂\mathbf{x} ^2})^{−1}∇F(\mathbf{x} ))>0 $$
✅牛顿法不一定收敛,\(\mathbf{H}\)正定场景牛顿法一定收敛。
- Any method using a positive definite matrix P to modify the gradient yields a descent method:
$$\mathbf{d} (\mathbf{x} )=−\mathbf{P} ^{−1}∇F(\mathbf{x} ) \quad \Rightarrow \quad −∇F(\mathbf{x} )\cdot (−\mathbf{P} ^{−1}∇F(\mathbf{x} ))>0 $$
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/