GAMES103

P32

Impact Zone Optimization

The goal of impact zone optimization is to optimize \(\mathbf{x}^{[1]}\) until it becomes intersection-free. (This potentially suffers from the tunneling issue, but it’s uncommon.)

tunneling issue 是指：\(\mathbf{x} ^{[1]}\) 离两个安全区都比较近。\(\mathbf{x} ^{[0]}\) 在其中一个安全区，而\(\mathbf{x} ^{[1]}\) 被优化到了另一个安全区。表现出的现象为穿透。

带约束优化问题

目标优化：

$$ \bar{\mathbf{x} }^{[1]}\longleftarrow \mathrm{argmin} _\mathbf{x}  \frac{1}{2} ||\bar{\mathbf{x} }-\mathbf{x}^{[1]}||^2 $$

约束：

$$ \text{such that} \begin{cases} C(\mathbf{x} )=−(\mathbf{x} _3−b_0\mathbf{x} _0−b_1\mathbf{x} _1−b_2\mathbf{x} _1)\cdot \mathbf{N} ≤0 & \text{ For each detected vertex-triangle pair } \\ C(\mathbf{x} )=−(b_2\mathbf{x} _2+b_3\mathbf{x} _3−b_0\mathbf{x} _0−b_1\mathbf{x} _1)\cdot \mathbf{N}≤0 & \text{ For each detected edge-edge pair } \end{cases} $$

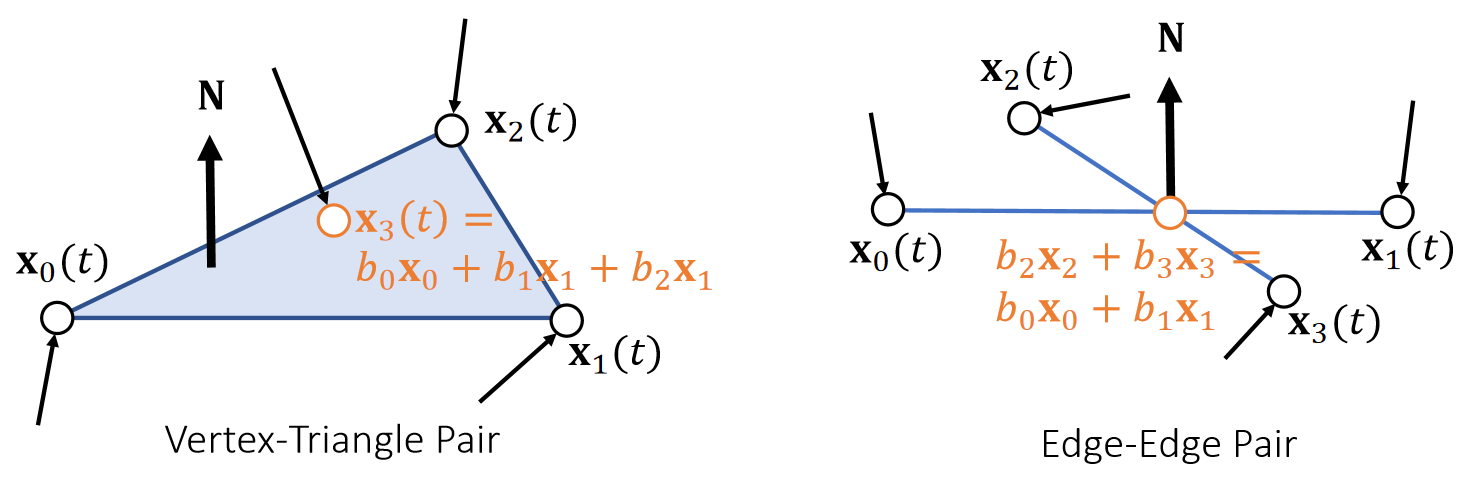
这是一个带约束优化问题。　　　

带约束优化问题转为无约束优化问题　　　

P36

We can then convert it into an unconstrained form:

$$\bar{\mathbf{x} } {[1]}\longleftarrow \text{argmin}_{x,λ}(\frac{1}{2} ||\mathbf{x} −\mathbf{x} ^{[1]}||^2+\frac{ρ}{2} ||\text{max}(\tilde{C} (\mathbf{x} ))||^2−\frac{1}{2ρ}||\mathbf{λ} ||^2) $$

$$ \tilde{C} (\mathbf{x})= \text{max}(\mathbf{C} (\mathbf{x} )+\mathbf{λ} /ρ) $$

Augmented Lagrangian:

\(\mathbf{x} ^{(0)} \longleftarrow \mathbf{x} ^{[0]}\)
\(\mathbf{λ \longleftarrow 0} \)
For \(k=0…K\)
$$\mathbf{x} ^{(k+1)} \longleftarrow \mathbf{x} ^{(k)}−α∇(\frac{1}{2} ||\mathbf{x} −\mathbf{x} ^{[1]}||^2+\frac{ρ}{2} ||\text{max}(\tilde{C} (\mathbf{x} ))||^2−\frac{1}{2ρ}||\mathbf{λ} ||^2)$$
\(λ\longleftarrow ρ\tilde{C} (\mathbf{x} )\)
\(\bar{\mathbf{x} } ^{[1]}\longleftarrow \mathbf{x} ^{(k+1)}\)

Tang et al. 2018. I-Cloth: Incremental Collision Handling for GPU-Based Interactive Cloth Simulation. TOG. (SIGGRAPH Asia)

P37

About Impact Zone Optimization

• Fast per iteration

  • Only have to deal with vertices in collision.

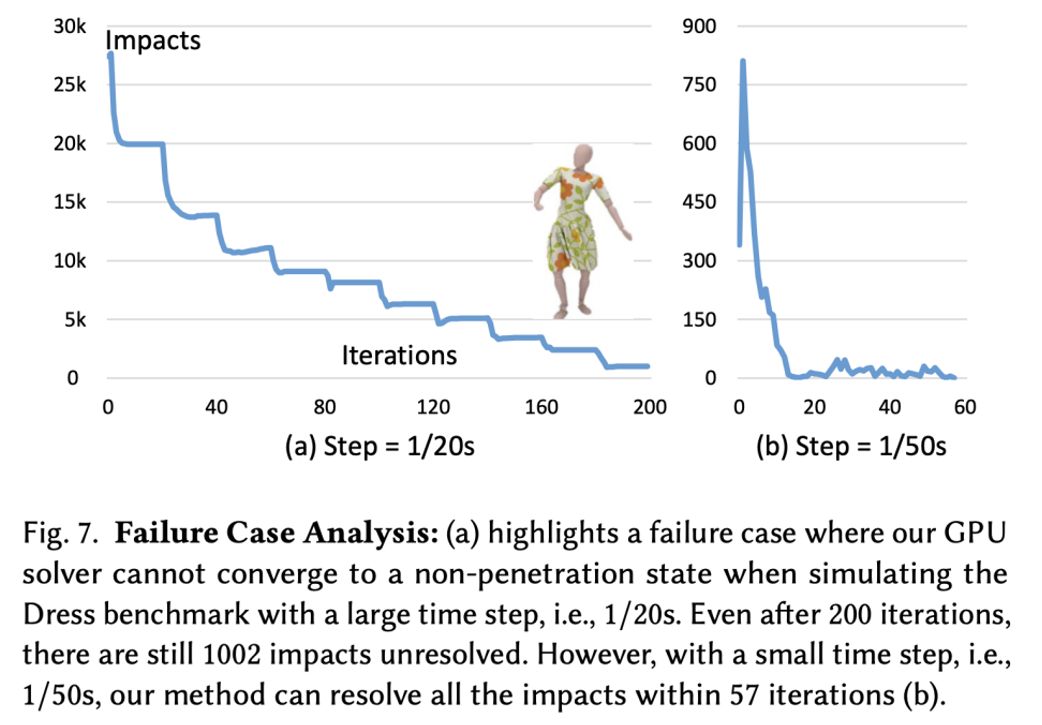
• Convergence sensitive to \(||\mathbf{x} ^{[0]}−\mathbf{x} ^{[1]}||^2\), or the time step \(∆t\)

  • Can take many iterations to, or never achieve intersection-free.
  • Easy solution is to reduce \(∆t\), but that increases total costs.

P33

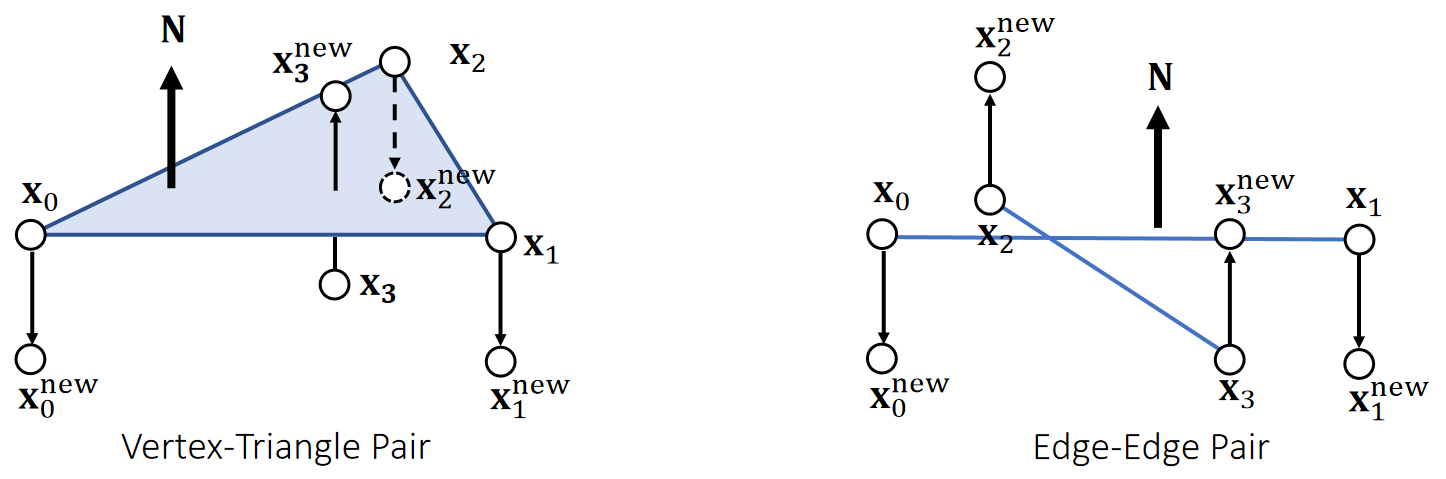
Every pair gives new positions to the involved vertices. We can combine them together in a Jacobi, or Gauss-Seidel fashion, just like position-based dynamics.

P34

After-Class Reading (Cont.)

Bridson et al. 2002. Robust Treatment of Collisions, Contact and Friction for Cloth Animation. TOG (SIGGRAPH).

Relative simple explicit integration of cloth dynamics

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/