流体力学

流体力学将物体建模为物质在其体内连续分布的实体，称为流体微团。

连续性方程描述了物理量在时空中的输运

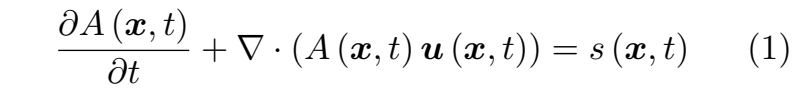
其中：

A 可为任意标量、矢量或张量形式的物理属性，
u 表示速度，
s 是 A 的源项，
所有这些量均定义于时间 t 和位置 x。

公式 (1) 表明，在固定位置处任何物理属性的变化率 ∂A/∂t 取决于 Au 通量所带来的变化以及源项 s 的贡献。

针对公式 (1) 中的物理属性 A，流场可从拉格朗日或欧拉视角进行分析：

欧拉视角 基于固定位置来研究物理属性的变化。在给定位置 x 处物理量 A 的变化率即为公式 (1) 中的 ∂A(x, t)/∂t 项。虽然直观，但这一视角并未显式表达连续介质假设中流体微团的运动，因为微团始终在不同时刻流经固定的空间位置。

拉格朗日视角 通过将公式 (1) 改写为以下形式，研究流体微团的物理属性变化：

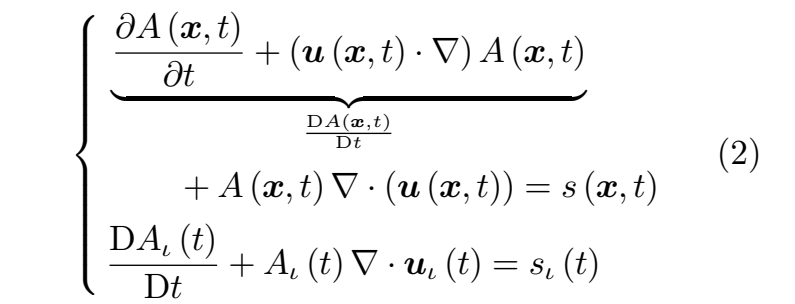
其中 D(·)/Dt 即所谓的物质导数，表示流体微团内物理量 A 的变化率。

纳维-斯托克斯方程

纳维-斯托克斯方程描述了流体流动的动力学规律，是流体仿真的根本基础。

质量守恒

在封闭系统中，流体的质量随时间保持守恒。该原理由连续性方程（公式（2））表示。令 A 为流体密度，并设 s ≡ 0，则公式（2）可改写为：

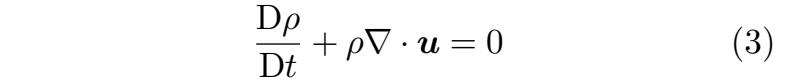
在不可压缩流动的情况下，流体内的密度变化保持恒定，即 Dρ/Dt = 0。该条件进一步意味着速度场无散度，其表达式为：

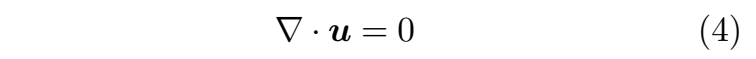
纳维-斯托克斯动量方程

为进一步描述不可压缩流体流动的运动特性，可对每个流体微团的动量进行分析。将动量项 ρu 代入公式（1），并利用公式（2），可得：

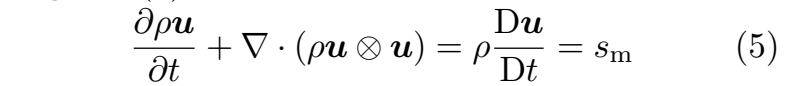
其中 sm 是改变各流体微团速度的动量源项，符号 ⊗ 表示外积运算。在此基础上，黏性可压缩流的纳维-斯托克斯动量方程基本形式进一步将 sm 具体表述为三个独立项：

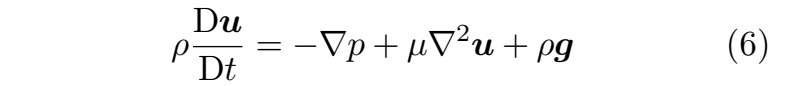
其中 p 表示压力，g 为重力加速度，µ 是描述流体粘性程度的动态粘性系数。公式（6）表明，流体微团的速度变化率受三个力项的影响：压力项（−∇p）、粘性项（µ∇2u） 以及重力项（ρg）。

从 NS 到浅水方程

纳维-斯托克斯方程是三维流场的完整描述，但直接求解代价很高。**浅水方程（Shallow Water Equations）**是它针对「薄层流体」的一种近似降维：假设流动发生在薄层内（水平尺度 ≫ 深度），把三维问题压缩成「每个位置一个高度 + 一个水平平均速度」。它不是新物理，而是 NS 方程在特定假设下的严格推论。

核心假设：静水压强分布

对 NS 方程做降维的关键一步，是给压强 p 一个可积分的形式。完整 NS 里压强是未知场（要靠泊松方程解出来）；浅水近似假设：

压强只由该点到水面的距离决定——某点承受的只是「从它到水面之间那一段水的重量」，水平方向压强处处一致：

$$ p(x, z) = \rho g ,\big(s(x) - z\big) $$

其中 s(x) 是水面高度，z 是该点的竖直坐标（向上为正）。这个假设的物理依据是：竖直方向上流体处于（近似）静力平衡，NS 竖直分量的重力项与压强梯度项相消。

✅ 这一步正是「让积分能算」的开关：压强不再是未知量，而是高度 s 的已知函数。NS 中最难解的部分（压强泊松方程）被一个代数式替代了。

压强项的水平梯度：沿深度积分

有了 p 的表达式，就可以计算 NS 水平分量的压强项。对一段水深（从底 b 到水面 s）积分：

$$ \int_b^{s} \frac{\partial p}{\partial x}, dz ;=; \int_b^{s} \rho g \frac{\partial s}{\partial x}, dz ;=; \rho g (s - b),\frac{\partial s}{\partial x} $$

令水深 h = s − b，除以 h 得到深度平均后的水平压强梯度：

$$ \frac{1}{h}\int_b^{s} \frac{\partial p}{\partial x}, dz ;=; \rho g \frac{\partial s}{\partial x} $$

注意结果的形态：压强梯度只依赖水面坡度 ∂s/∂x，与压强在深度内怎么分布无关（静水压线性分布的积分恰好抵消成均匀项）。这就是「薄层流动里水从高处往低处加速」的数学表述——驱动力正比于水面斜率。

$$ \frac{\partial h}{\partial t} + \frac{\partial (h\bar{u})}{\partial x} = 0 \qquad\qquad \frac{\partial \bar{u}}{\partial t} + \bar{u}\frac{\partial \bar{u}}{\partial x} = -g\frac{\partial s}{\partial x} $$

第一个方程（质量/体积守恒）：水柱高度的变化 = 净流入量，h·ū 是单位宽度截面的体积通量；
第二个方程（动量守恒）：水平平均速度 ū 的变化由水面坡度驱动，ū·∂ū/∂x 是平流项（水带着自己的速度流动）；
s = b + h：若底面平坦（b 常数），∂s/∂x = ∂h/∂x，方程组完全以 h 和 ū 为未知量封闭。

与完整 NS 对比，损失的只有三样：竖直方向的结构（速度剖面被压平为 ū）、竖直加速度（自由面不再翻卷）、以及垂向压强的非静水分量（快速流动时误差来源）。换来的代价优势是：未知量从 4 个三维场（u, v, w, p）降到 2 个一维场（h, ū），且无需解压强泊松方程。

与本课程高度场章节的关系

高度场模型求解的就是这套浅水方程：其「高度场更新」对应第一个方程，「速度场更新」对应第二个方程（课程版本忽略了平流项并消去 ū，得到单个二阶波动方程 d²h/dt² = (h/ρ)·∂²P/∂x² 的简化形式，便于引入空间离散化）。两处方程的差异只是「是否保留平流」的课程简化，物理假设同源：静水压分布 + 薄层深度平均。

从连续统到动理学

以上讨论全部建立在连续介质假设之上：流体被建模为连续分布的流体微团，未知量是密度 ρ(x, t) 与速度 u(x, t) 这类宏观量，演化方程是 Navier-Stokes 方程。

若把观察层级下移一层，流体由大量分子构成，每个分子有自己的位置与速度。此时可以用速度分布函数描述流体：

\[f(\mathbf{x}, \boldsymbol{\xi}, t)\]

它的含义是：在时刻 t、位置 x 附近单位体积内，速度落在 ξ 附近单位速度区间内的分子数。与连续统描述相比，它多保留了一个速度维度的自变量。

宏观量是分布函数的矩：

\[\rho = \int f , d\boldsymbol{\xi}, \qquad \rho\mathbf{u} = \int \boldsymbol{\xi} f , d\boldsymbol{\xi}\]

也就是说，只要知道 f，Navier-Stokes 方程中的宏观量都能由积分得到。这一步是动理学与连续统之间的接口。

f 的演化由玻尔兹曼输运方程给出：

\[\frac{\partial f}{\partial t} + \boldsymbol{\xi}\cdot\nabla_{\mathbf{x}} f = \Omega(f)\]

左端对应分子在无碰撞情况下的自由飞行；
右端 Ω(f) 是碰撞算子，描述分子间碰撞引起的分布变化。

碰撞不产生也不消灭质量与动量，因此 Ω(f) 关于 ξ 的零阶矩与一阶矩均为零。对玻尔兹曼方程两端关于 ξ 取矩，即可得到宏观的连续性方程与动量方程——这是"从动理学还原到连续统"的基本途径。完整推导还需要配合 Chapman-Enskog 展开：把 f 按小参数展开并逐阶分离，零阶给出无粘的欧拉方程，一阶给出粘性应力张量，二阶还原出完整的 Navier-Stokes 方程。

完整碰撞算子是复杂的积分，工程上常用 BGK 近似（Bhatnagar-Gross-Krook, 1954）：

\[\Omega(f) \approx -\frac{1}{\tau}\left(f - f^{eq}\right)\]

即分布 f 以时间常数 τ 松弛到局部平衡分布 f^eq：

τ 大 → 松弛慢 → 粘性大
τ 小 → 松弛快 → 粘性小

这一近似把碰撞算子从积分运算简化为一次代数插值，是后面格子玻尔兹曼方法能够高效实现的关键。

三层描述对照

层级	描述变量	演化方程	对应方法
连续统（宏观）	$\rho, \mathbf{u}$	Navier-Stokes	有限差分 / 有限体积 / 有限元 + 投影法
动理学（介观）	$f(\mathbf{x},\boldsymbol{\xi},t)$	玻尔兹曼输运方程 + BGK	格子玻尔兹曼方法 LBM
分子（微观）	每个分子的位置与速度	牛顿第二定律	分子动力学 MD

本节内容属于物理基础，只说明动理学的描述层级与它和连续统的还原关系。对应的数值离散方案（格子气自动机与格子玻尔兹曼方法）见格子动理学方法，其中动理学基础一节给出了本节内容的完整推导。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES103_mdbook/