Newton-Raphson Method

x是值的F(x)函数

The Newton-Raphson method, commonly known as Newton’s method, solves the optimization problem: \(x^{[1]}\) = argmin \(F(x)\).

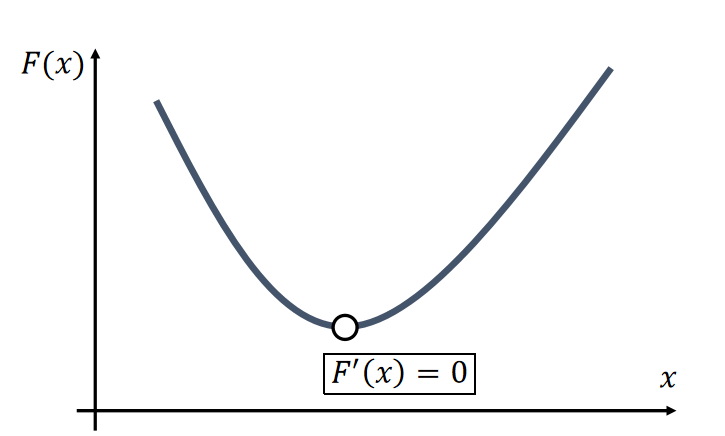
Given a current \(x^{(k)}\), we approximate our goal by:

$$ 0={F}' (x)≈{F}'(x^{(k)})+{F}'' (x^{(k)})(x−x^{(k)}) $$

✅ \(a = \min F(x)⇒ F'(a)= 0\)，\({F}' (x)\) 是非线性函数，直接解\({F}' (x)=0\) 很难解
✅ 对\({F}'(x)\) 做一阶泰勒展开，保留到二阶项。
✅ 假设\(x^{[k]}\)为任意已知值，就变成了解线性方程，很容易解出\(x\).
✅ 因为\({F}'(x)\) 是一个近似的，\(x\) 也是一个近似解。但\(x^{[k]}\) 越接近真实解，\(x\) 也会越接近真实解。因此，选代是\(x^{[k]}\)和\(x\) 都不断逼近真实解的过程。
✅ 普通的梯度下降是把\({F}' (x)\) 近似到一阶，牛顿法是近似到二阶，因此下降更快。

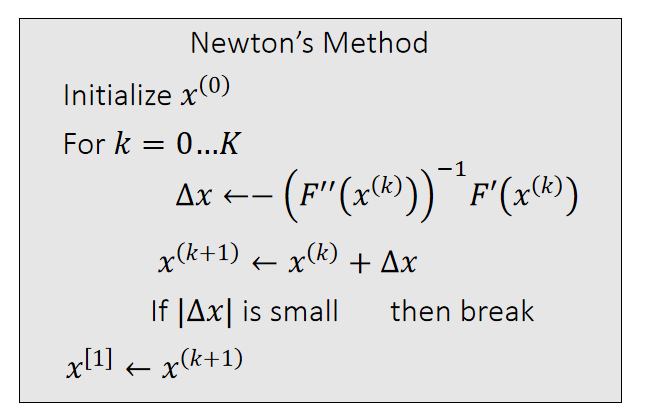
✅ Overshooting 的本质：误差会积累和放大

P16
Newton’s method finds an extremum, but it can be a minimum or maximum.

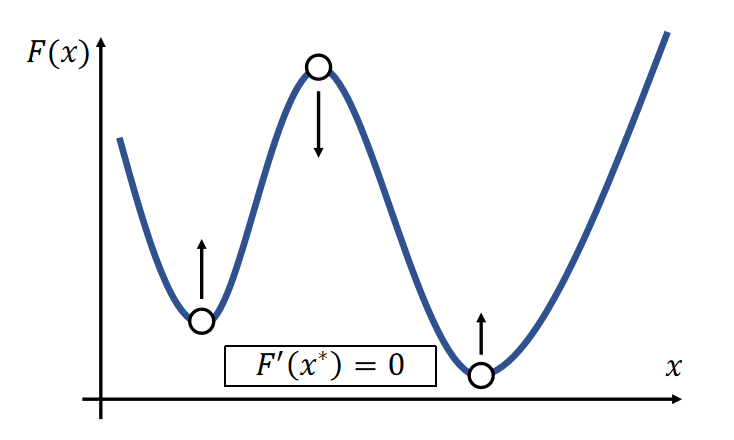
• At a minimum \(x^∗, {F}'' (x^∗)>0\).
• At a maximum \(x^∗, {F}''(x^∗)<0\).
• If \({F}''(x)>0\) is everywhere, \(F(x)\) has no maximum. \(=> F(x)\) has only one minimum.

✅ \(F'(a)= 0,a\) 有可能是最大值或最小值，因此要判定解是否合理。判定方法： \({F}''(x)\)

P17

x是向量的F(x)函数

Now we can apply Newton’s method to: \(x^{[1]} \)= argmin \(F(x)\). Given a current \(x^{(k)}\), we approximate our goal by:

$$ 0=\nabla F( \mathbf{x}) ≈\nabla F (\mathbf{x} ^{(k)})+\frac{∂F ^2(\mathbf{x} ^{(k)})}{∂\mathbf{x} ^2} (\mathbf{x−x} ^{(k)}) $$

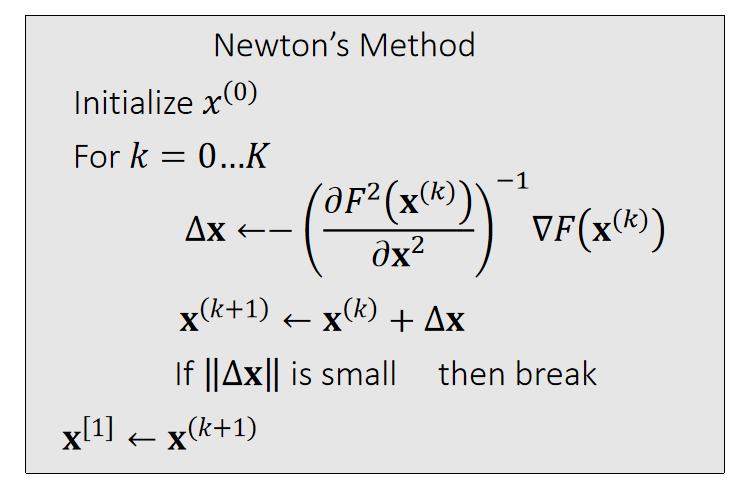
✅ 按照 \(\Delta x\) 的更新公式，只需要用到\(F'(x)\) 和 \({F}''(x)\)， 不需要知道 \(F(x)\).
✅ 此处\(x\)是向量，因此\(F'(x)\)是向量，\({F}''(x)\)是 Hession 矩阵

[TODO]怎么保证 \(\mathbf{x}\) 收敛