4. 任意拉格朗日-欧拉法(Arbitrary Lagrangian-Eulerian, ALE)
- 原理:网格可随物质运动(拉格朗日)或固定(欧拉),也可任意移动以兼顾两者优点。通常与粒子结合用于处理大变形或界面问题。
- 结合方式:在变形过大区域将材料转为粒子,避免网格畸变。
- 应用:爆炸、冲击、金属成型等固体力学问题。
5. 耦合粒子-网格法(Coupled Particle-Grid Methods)
- 离散元法(DEM)与有限元法(FEM)耦合:
- 颗粒物质(DEM粒子)与连续体(FEM网格)交互,用于模拟颗粒-结构相互作用。
- 光滑粒子流体动力学(SPH)与网格耦合:
- 近界面区域用SPH(粒子法),远处用网格法(如FVM),提高计算效率。
6. 其他混合方法
- 分子动力学(MD)与连续体耦合:
- 微观区域用MD(粒子),宏观区域用有限元网格,通过重叠区交换信息。
- 蒙特卡洛粒子与网格耦合:
- 在辐射传输、稀薄气体动力学中,粒子跟踪与网格场计算结合。
总结
选择依据
| 方法 | 适用领域 | 主要优点 |
|---|---|---|
| PIC | 等离子体、电磁场 | 场求解稳定,粒子自由度灵活 |
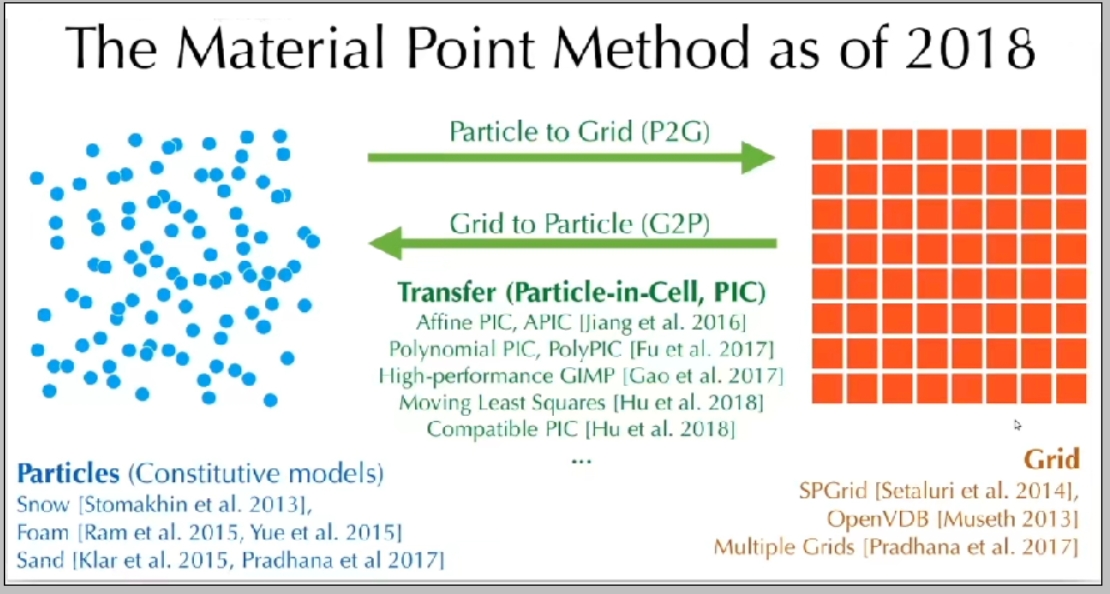
| MPM | 固体大变形、多相材料 | 避免网格畸变,适合历史相关材料 |
| FLIP/PIC | 不可压缩流体 | 细节保留好,适合动画 |
| ALE | 冲击、流固耦合 | 自适应网格,兼顾精度与变形 |
| DEM-FEM | 颗粒-结构相互作用 | 离散与连续介质自然耦合 |
flowchart LR
A[时空采样优化]
A --> B[时间自适应]
A --> C[空间自适应]
B --> D[全局自适应]
B --> E[局部自适应]
C --> F[欧拉法]
C --> G[拉格朗日法]
C --> H[混合法]
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/