P39
Shape Matching
✅ Shape Matching 跳过了。
先让每个粒子独立仿真,也不需要考虑弹簧力。
将每个面片的变形程度构建为能量,通过优化能量的方式使 Mesh 减少形变,所有面片以统一的方式进行优化,因此是一种全局优化方法。
P40
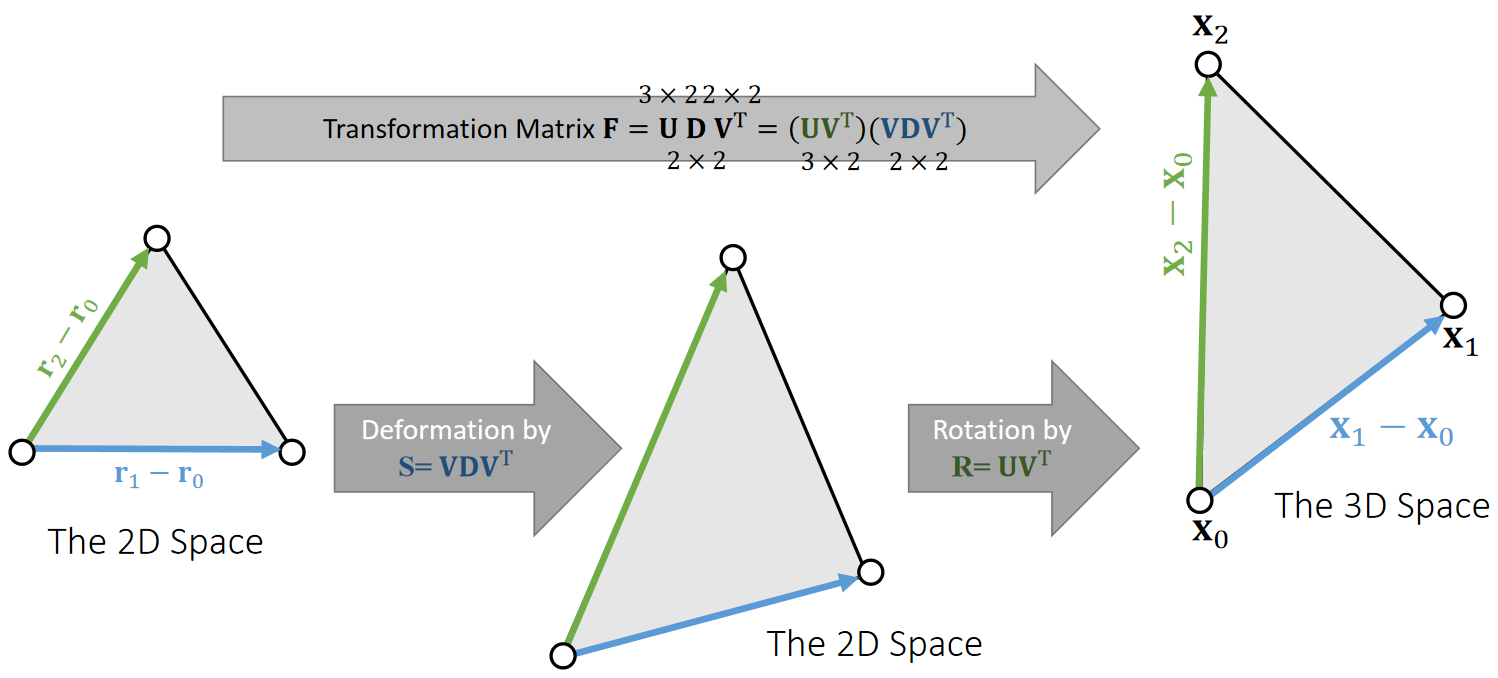
量化变形
The basic idea is to define a quadratic energy based on the rotated reference element. To do so, we split transformation into deformation + rotation.
有两种方式基于能量恢复形变。
- 向能量减少的方向优化。
- 转化为力,基于力进行仿真。

P41
P42
计算能量
We can then define the quadratic energy as:
$$ E (\mathbf{x} )=\frac{1}{2}||\mathbf{F−R} ||^2 $$
(\(\mathbf{R}\) is the rotation inside of \(\mathbf{F}\). This energy tries to penalize the existence of \(\mathbf{S}\)).
Assuming that \(\mathbf{R}\) is constant, this \(E(\mathbf{x})\) becomes a quadratic function. We can then derive the force and the Hessian.
$$ E(\mathbf{x} ) =\frac{1}{2} ||\begin{bmatrix} \mathbf{x} _1-\mathbf{x} _0 &\mathbf{x} _2-\mathbf{x} _0 \end{bmatrix}\begin{bmatrix} \mathbf{r} _1-\mathbf{r} _0 &\mathbf{r} _2-\mathbf{r} _0 \end{bmatrix}^{−1}−\mathbf{R}||^2 $$
P43
A Summary For the Day
-
A mass-spring system
- Planar springs against stretching/compression \(\quad\)- replaceable by co-rotational model
- Bending springs \(\quad\)- replaceable by dihedral or quadratic bending
- Regardless of the models, as long as we have \(E (\mathbf{x})\), we can calculate force \(\mathbf{f} (\mathbf{x} )=−∇ \mathbf{E} (\mathbf{x})\) and Hessian \(\mathbf{H} (\mathbf{x} )=∂E^2(\mathbf{x} )/∂\mathbf{x} ^2\). Forces and Hessians are stackable.
-
Two integration approaches
- Explicit integration, just need force. Instability
- Implicit integration, as a nonlinear optimization problem
- One way is to use Newton’s method, which solves a linear system in every iteration:
$$ (\frac{1}{∆t^2}\mathbf{M} +\mathbf{H} (\mathbf{x} ^{(k)}))∆\mathbf{x} =− \frac{1}{∆t^2} \mathbf{M} (\mathbf{x} ^{(k)}−\mathbf{x} ^{[0]}−∆t\mathbf{v} ^{[0]})+\mathbf{f} (\mathbf{x} ^{(k)}) $$
- There are a variety of linear solvers (beyond the scope of this class).
- Some simulators choose to solve only one Newton iteration, i.e., one linear system per time step.
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/