基于物理的数学模型
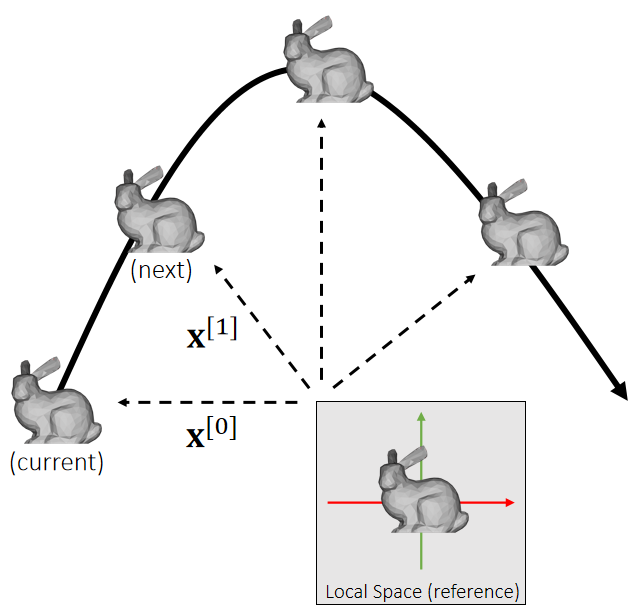
For translational motion, the state variable contains the position x and the velocity v.
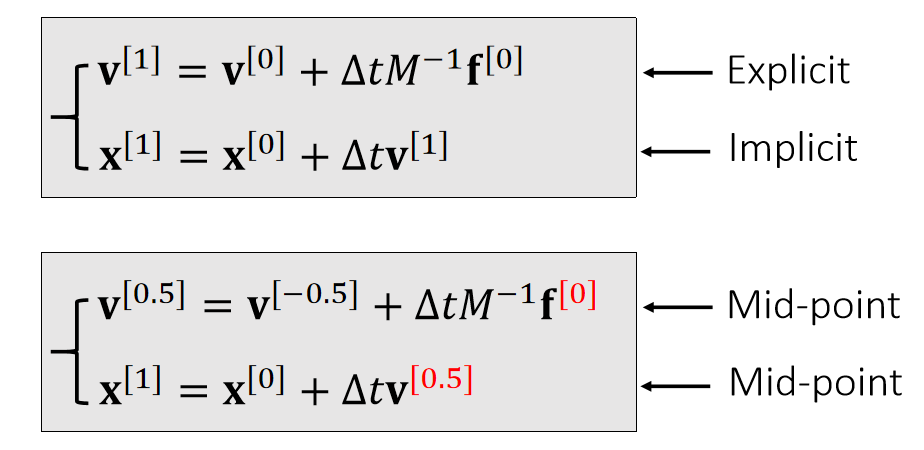
{v(t[1])=v(t[0])+M−1∫t[1]t[0]f(x(t),v(t),t)dtx(t[1])=x(t[0])+∫t[1]t[0]v(t)dt
✅ 也可以用˙x表示速度v
速度是加速度的积分,因此Δt=∫a=∫FM=M−1∫F.
位置是速度的积分
本质上是解积分
💡 积分的过程比较独立,单独放在最后link,避免破坏整体的结构性。最后结论是混合式的积分方法。
P17
Types of Forces

✅ 在做模拟时,如果不要求能量守衡,出于问题简化的目的,直接对速度做衰减,代替引入阻力
P18
Rigid Body Simulation Pipeline (Translation Only)


The mass M and the time step Δt are user-specified variables.
✅ 实际应用中,Δt 要跟帧率匹配
质量 M 可以是个对角矩阵或实数
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/