P16
SPH-Based Fluids
P17
Fluid Dynamics
- We model fluid dynamics by applying three forces on particle i.
- Gravity
- Fluid Pressure
- Fluid Viscosity
P18
Gravity Force
- Gravity Force is:
$$ \mathbf{F} _ \mathbf{i}^ \mathbf{gravity} = m _i \mathbf{g} $$
P19
Pressure Force
✅ 要解决的问题:怎么计算压强?怎么把压强转化为力?
怎么计算压强
-
Pressure is related to the density
- First compute the density of Particle i:
$$ \rho _ i = \sum _ j m _ j W _ {ij} $$
- Convert it into pressure (some empirical function):
$$ P_i=k((\frac{\rho _i}{\rho _\mathrm{constant } } )^7-1) $$
✅ 密度到压强的计算是一个经验公式。
压强转化为力
P20
- Pressure force depends on the difference of pressure:

P21
- Mathematically, the difference of pressure => Gradient of pressure.
$$ \mathbf{F} _i^{pressure}=-V_i\nabla _iP^{smooth} $$
✅ 体积为粒子在空间中占有的体积,体积越大受到的压力越大、\(\nabla\)代表压强的差。
- To compute this pressure gradient, we assume that the pressure is also smoothly represented:
$$ P_i^{smooth}= \sum _ j V_jP_j W_{ij} $$
✅ 假设空间是一个压强场、粒子是空间中的采样。\(P^{smooth}\)是通过周粒子\(P\)的插值得到的采样点压强。
- So:
$$ \mathbf{F} _ i^{pressure} = - V _ i \sum _ j V _ j P _ j \nabla _ i W _ {ij} $$
P22
Viscosity Force
粘滞所产生的效果
- Viscosity effect means: particles should move together in the same velocity.
- In other words, minimize the difference between the particle velocity and the velocities of its neighbors.
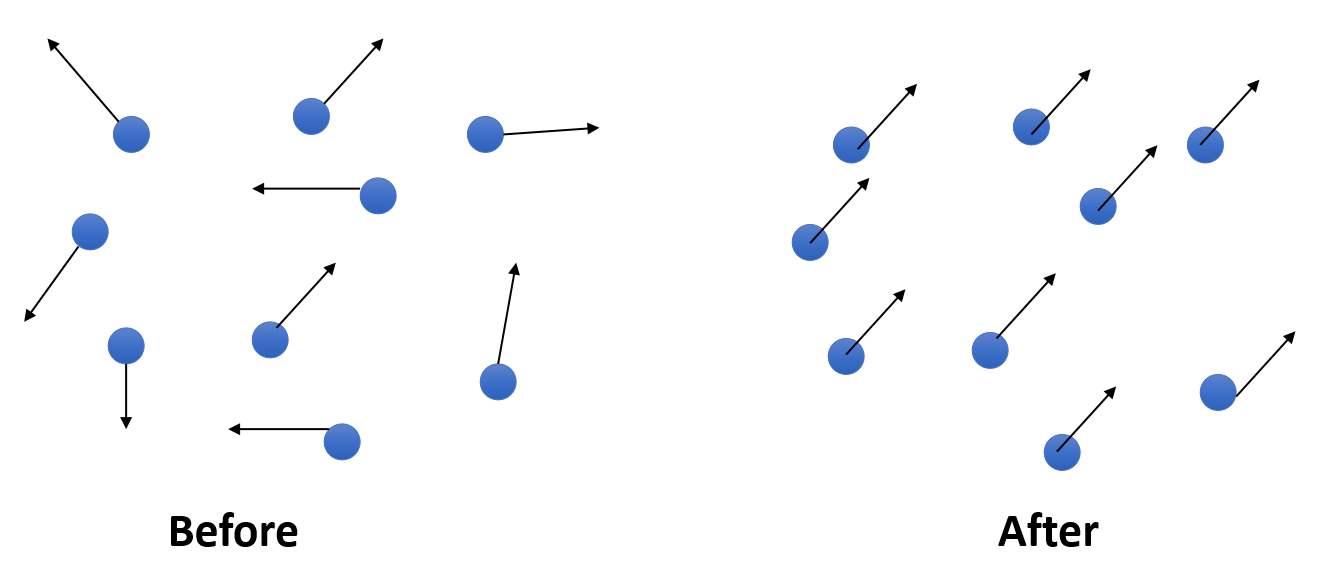
✅ Viscosity (粘滞)类似于 damping (阻尼),但有些区别,后者的目标是让粒子的运动停下来,前者的目的是让所有粒子的运动整齐划一,即速度差趋于0.
P23
粘滞力 Viscosity Force
- Mathematically, it means:
$$ \mathbf{F} _i^{vis \cos ity}=-\nu m_i\Delta _i\mathbf{V} ^{smooth} $$
✅ \(V\):粘滞系数, \(\nabla V\):速度的 Laplacian.注意速度是3D矢量。
- To compute this Laplacian, we assume that the velocity is also smoothly represented:
$$ \mathbf{V} _i^{smooth}= \sum_jV_j \mathbf{v} _ j W _ {ij} $$
- So:
$$ \mathbf{F} _i^{vis \cos ity}=-\nu m_i\sum _jV_j\mathbf{v} _j\Delta _iW _{ij} $$
✅ smooth会产生粘滞的效果。
P24
Algorithm
- For every particle i
- Compute its neighborhood set
- Using the neighborhood, compute:
- Force = 0
- Force + = The gravity force
- Force + = The pressure force
- Force + = The viscosity force
- Update \(v_i = v_i + t * \text{ Force } / m_i\);
- Update \(x_i = x_i + t * v_i\);
| $$ \color{Red}{ \text{ What is the bottleneck of the performance here?}} $$ |
|---|
✅ 性能瓶颈:计算邻居,因为总粒子数为百万级。
Spatial Partition加速求最近邻
P25
Exhaustive Neighborhood Search
- Search over every particle pair? O(\(N^2\))
- 10M particles means: 100 Trillion pairs…
P26
Solution: Spatial Partition
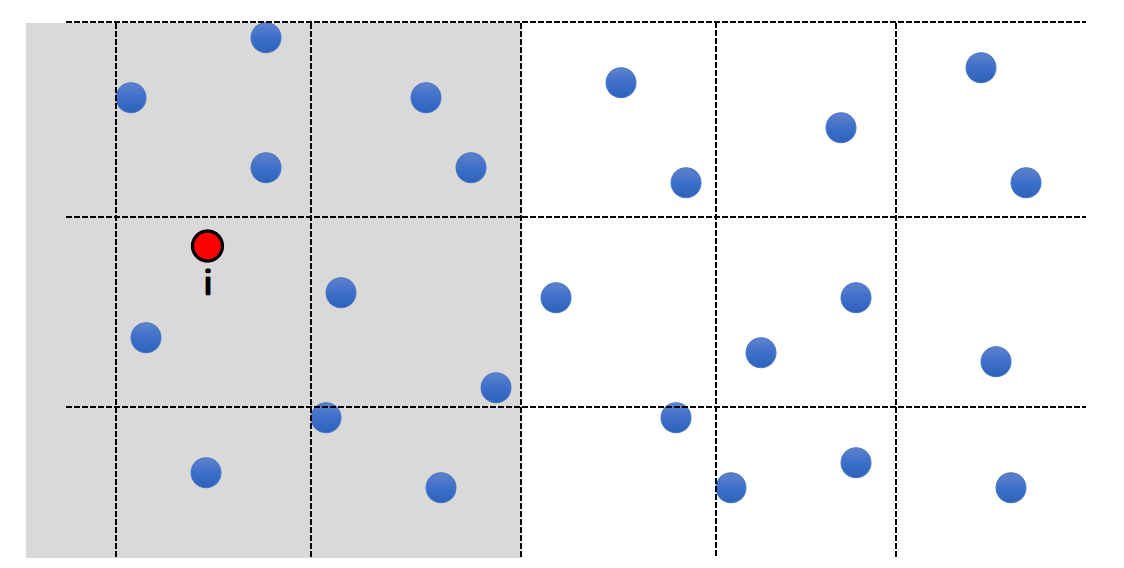
- Separate the space into cells
- Each cell stores the particles in it
- To find the neighborhood of i, just look at the surrounding cells
P27
Spatial Partition
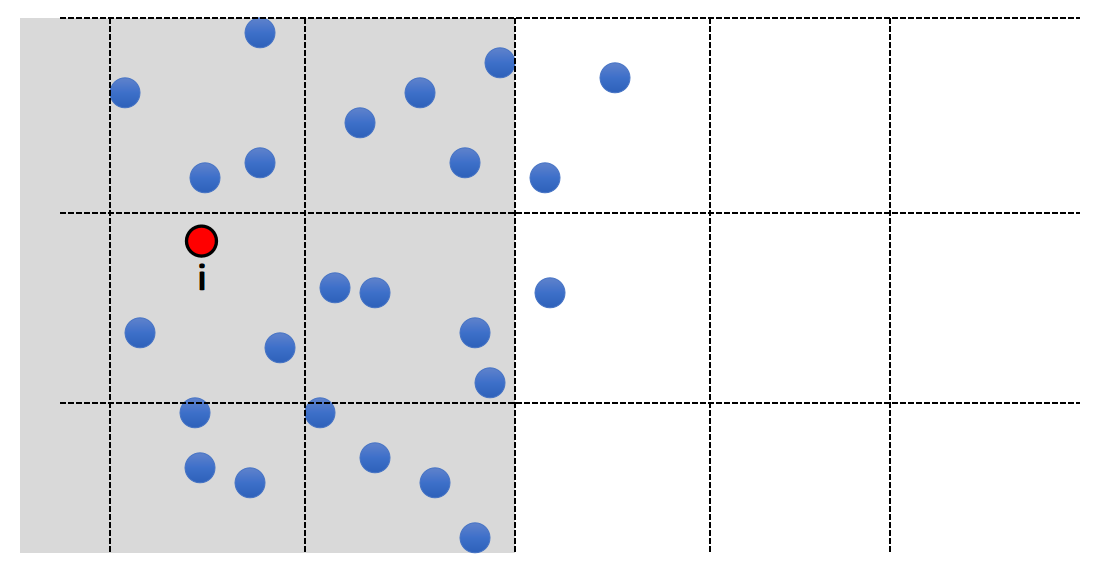
- What if particles are not uniformly distributed?
✅ 例如水花喷溅的效果,通常靠近水面的粒子小一点,更利于表现细节。
- Solution: Octree, Binary Spatial Partitioning tree…
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES103_mdbook/