Quaternion 四元数
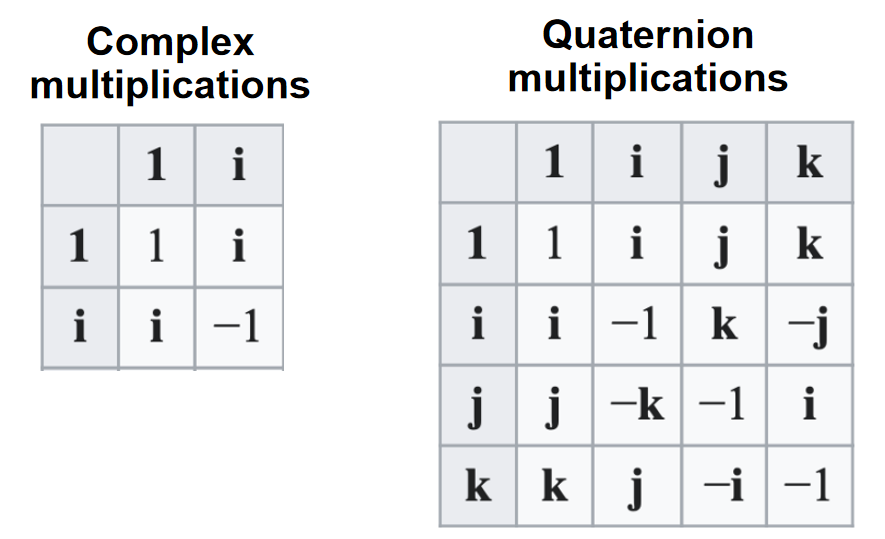
在数学中,四元数系统扩展了复数。 四元数由爱尔兰数学家威廉·罗文·Hamilton于 1843 年[1][2] 首次描述,并应用于三维空间的力学。 Hamilton将四元数定义为三维空间中两条有向线的商,[3] 或者等效地,定义为两个向量的商。 [4] 四元数的乘法是不可交换的。
📌
两个向量的商:最初引入四元数是为了定义向量的除法
四元数一般用以下形式表示
$$ {\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} } $$
其中 a、b、c 和 d 是实数; i, j, k 是基本四元数。
四元数用于纯数学,但在应用数学中也有实际用途,特别是用于涉及三维旋转的计算,例如三维计算机图形学、计算机视觉和晶体纹理分析。 [5] 它们可以与其他旋转方法一起使用,例如欧拉角和旋转矩阵,或者作为它们的替代方法,具体取决于应用程序。
定义
四元数的表达形式为
$$ {\displaystyle a+b,\mathbf {i} +c,\mathbf {j} +d,\mathbf {k} \ ,} $$
其中 a、b、c、d 是实数,i、j、k 是可以解释为指向三个空间轴的单位向量的符号。 在实际应用中,如果a、b、c、d之一为0,则省略对应项; 如果a、b、c、d都为零,则该四元数是零四元数,记为0; 如果 b、c、d 中的一个等于 1,则相应的项只写为 i、j 或 k。
或
$$ \mathbf{q} = \begin{bmatrix} \mathbf{s} &\mathbf{v} \end{bmatrix} $$
s为标量,v为向量
计算
\(a\mathbf{q} =\begin{bmatrix} as &a\mathbf{v} \end{bmatrix}\quad\) Scalar-quaternion Multiplication
\(\mathbf{q} _1±\mathbf{q} _2 =\begin{bmatrix} \mathbf{s}_1±\mathbf{s}_2 & \mathbf{v} _1 ± \mathbf{v} _2 \end{bmatrix}\quad\quad\) Addition/Subtraction
\(\mathbf{q} _1×\mathbf{q} _2= \begin{bmatrix} \mathbf{s} _1\mathbf{s} _2−\mathbf{v} _1\cdot \mathbf{v} _2 & \mathbf{s} _1\mathbf{v} _2+\mathbf{s} _2\mathbf{v} _1+\mathbf{v} _1×\mathbf{v} _2 \end{bmatrix}\quad\quad\) Multiplication
\(||\mathbf{q} ||=\sqrt{\mathbf{s^2+v\cdot v} } \quad\quad\)Magnitude
和分量标量乘法
📌
分量标量乘:依次让每个分量的系数与一个标量相乘。
标量即0维数字
$$ {\displaystyle \lambda (a+b,\mathbf {i} +c,\mathbf {j} +d,\mathbf {k} )=\lambda a+(\lambda b),\mathbf {i} +(\lambda c),\mathbf {j} +(\lambda d),\mathbf {k} .} $$
性质
不可交换:q2q1 != q1q2 结合:(q1q2)q3 = q1(q2q3) 满足乘法结合律和加法分配律
根据Hamilton 积的定义每个非零四元数都有逆:
$$ {\displaystyle (a+b,\mathbf {i} +c,\mathbf {j} +d,\mathbf {k} )^{-1}={\frac {1}{a^{2}+b^{2}+c^{2}+d^{2}}},(a-b,\mathbf {i} -c,\mathbf {j} -d,\mathbf {k} ).} $$
用四元数表示旋转
角轴转四元数
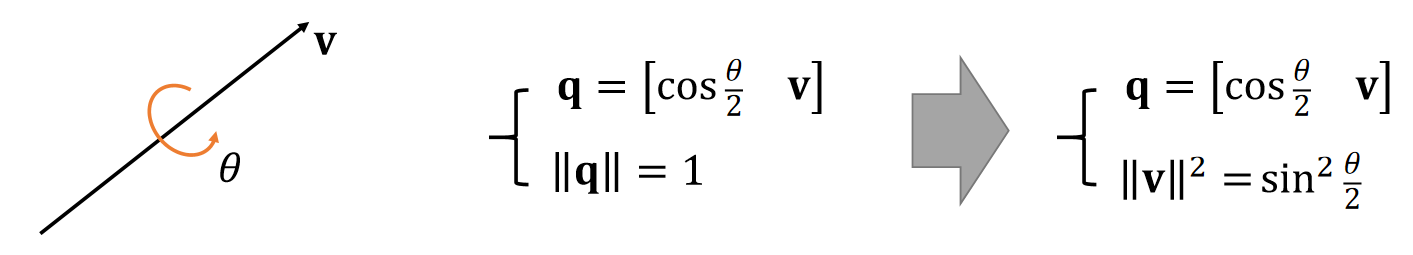
四元数转旋转
$$
\mathbf{R}=\begin{bmatrix}
s^2+x^2-y^2-z^2 & 2(xy-sz) & 2(xz+sy)\\
2(xy+sz) & s^2-x^2+y^2-z^2 & 2(yz-sx) \\
2(xz-sy) & 2(yz+sx) & s^2-x^2-y^2+z^2
\end{bmatrix}
$$
优势与局限性
优势
- 不易受到“万向节死锁”的影响。
- 比矩阵更快、更紧凑。
- 插值结果更稳定。