数值积分

显式积分与隐式积分

将连续积分转化为离散求和的计算方法，用于无法解析求解的积分问题。

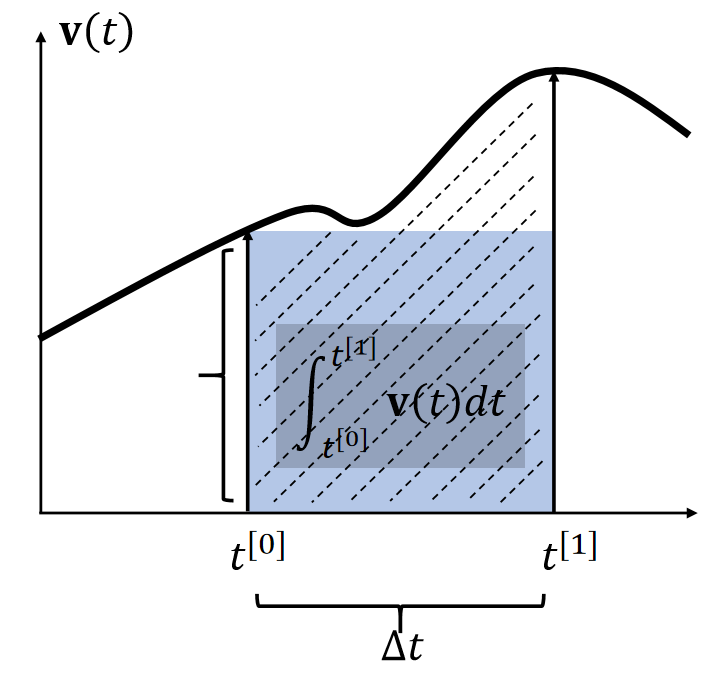
By definition, the integral \(\mathbf{x} (t) = \int \mathbf{v} (t) dt\) is the area. Many methods estimate the area as a box.

Explicit Euler	Implicit Euler	Mid-Point
显式积分	隐式积分
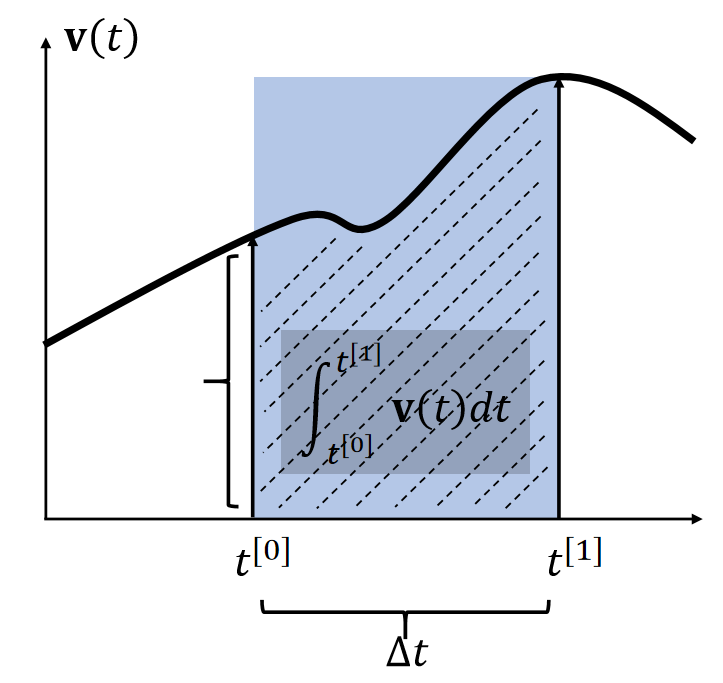
使用 \(t_0\) 时刻的速度作为box的高	使用 \(t_1\) 时刻的速度作为box的高
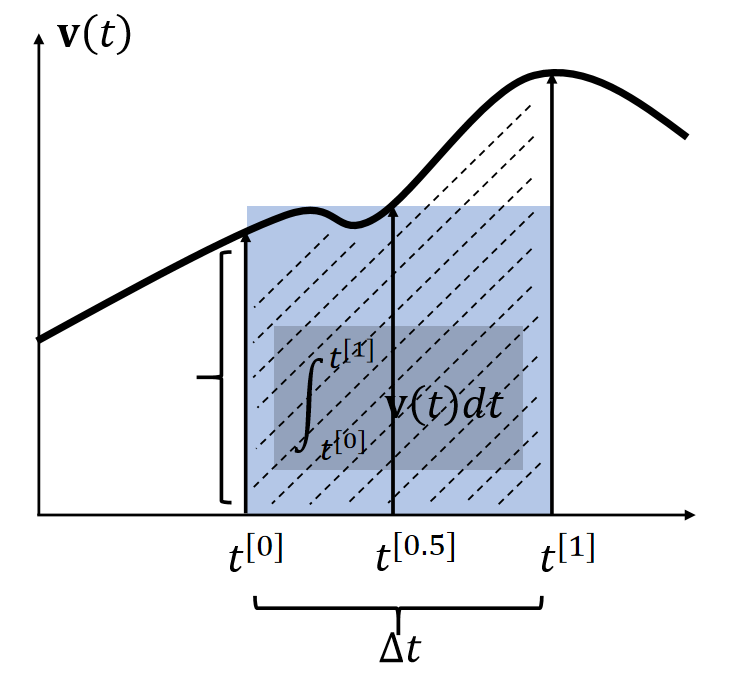
\(\int_{t^{[0]}}^{t^{[1]}} \mathbf{v} (t)dt≈∆t  \mathbf{v} (t^{[0]})\)	\(\int_{t^{[0]}}^{t^{[1]}} \mathbf{v} (t)dt≈∆t  \mathbf{v} (t^{[1]})\)	\(t^{[0]}\). \(\int_{t^{[0]}}^{t^{[1]}} \mathbf{v} (t)dt≈∆t  \mathbf{v} (t^{[0.5]})\)

✅ 假设\(\mathbf{x} \)和\(\mathbf{v} \)都是一维的。速度的积分就是阴影区域的面积。
✅ 近似到一阶项，因此称为一阶方法。漏掉的高阶项就是误差。
两种方法都只能一阶近似

P16

Leapfrog Integration

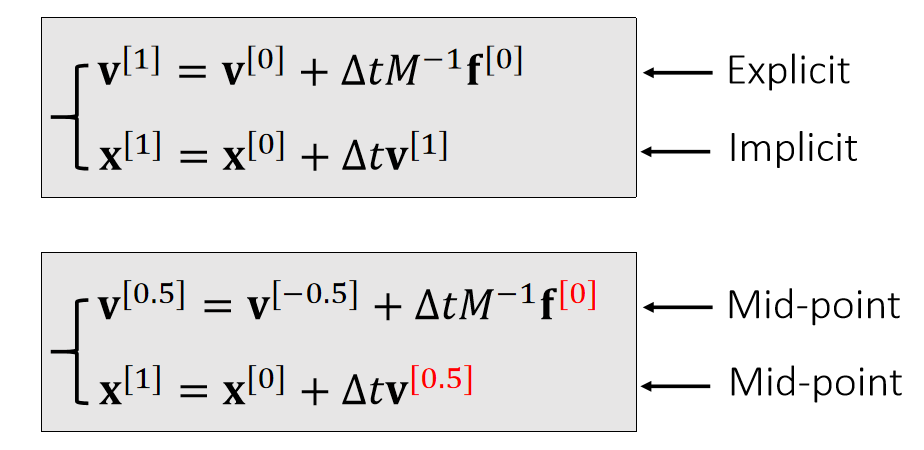
✅ 速度和位置是错开的。上下两种写法，在计算上是一样的。

In some literature, such a approach is called semi-implicit.

It has a funnier name: the leapfrog method.