导数代表函数增大的方向
在梯度下降法中,参数应该向导数的负方向移动。在梯度上升法中则相反。
临界点
一个函数在某个点上所有偏导都为0,这个点称为临界点(critical point)。
临界点有可能是:
- 极小值点 local/gobal minima
- 极大值点 local/global maxima
- 鞍点(saddle point)
| 名字 | name | 附近的点 | H矩阵的特征值 | 横截面 |
|---|---|---|---|---|
| 极小值点 | local/gobal minima | 所有点都比它大 | 全部为正 | 所有横截面上都是极小值点 |
| 极大值点 | local/global maxima | 所有点都比它小 | 全部为负 | 所有横截面上都是极大值点 |
| 鞍点 | saddle point | 某些点比它大,某些点比它小 | 有正有负 | 有的横截面上是极小值,有的横截面上是极大值 |
问:怎么区分一个临界点是什么类型?
答:Hessian矩阵。
Hessian矩阵区分临界点的类型
将$f(\theta)$在临界点处按泰勒公式展开并保留到二阶项,得:
$$
f(\theta) = f(\theta_0) + (\theta-\theta_0)g + \frac{1}{2}(\theta-\theta_0)^\top H(\theta-\theta_0) + ...
$$
已知:
H是一个对称矩阵,
由于$\theta$是临界点,一阶导数g为0
令$x=\theta-\theta_0$
得:
$$
f(\theta) = f(\theta_0) + \frac{1}{2}x^\top Hx + ...
$$
H正定 $\Rightarrow x^\top Hx > 0 \Rightarrow f(\theta) > f(\theta_0) \Rightarrow \theta_0$是局部极小点。
H负定 $\Rightarrow x^\top Hx < 0 \Rightarrow f(\theta) < f(\theta_0) \Rightarrow \theta_0$是局部极大点。
H[不定] $\Rightarrow x^\top Hx < 0$和$x^\top Hx > 0$都存在 $\Rightarrow f(\theta)$ 和$f(\theta_0)$关系不确定 $\Rightarrow \theta_0$是鞍点。
H非正定或非负定 $\Rightarrow$ 存在$x^\top Hx = 0$的情况 $\Rightarrow f(\theta) $和$f(\theta_0)$关系不确定,取决于被省略的二阶以上的项 $\Rightarrow$ 无法判断$\theta_0$是什么类型的点。
次导数(subderivative):
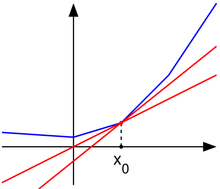
设f:I→R是一个实变量凸函数,定义在实数轴上的开区间内。这种函数不一定是处处可导的,例如最经典的例子就是f(x)=|x|,在x=0处不可导。但是,从下图的可以看出,对于定义域内的任何x0,我们总可以作出一条直线,它通过点(x0,f(x0)),并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数。
https://blog.csdn.net/qq_39521554/article/details/81877845