logistic sigmoid函数

$$\sigma(x) = \frac{1}{1+\exp(-x)}$$

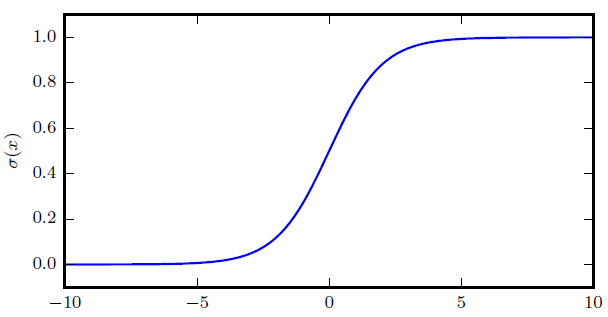
意义：

1. $$\sigma(x) \in (0, 1)$$
2. 通常用来产生Bernoulli分布中的参数 $$\phi$$
3. 当|x|非常大时会饱和，饱和是指 $$\sigma'(x)$$ 的变化非常缓慢。

softplus函数

$$\zeta(x) = \log(1+\exp(x))$$

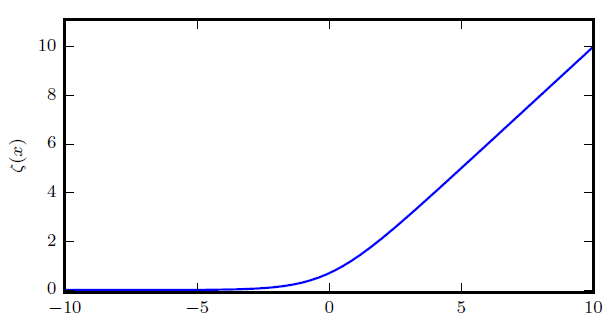
意义：

1. $$\zeta(x) \in (0, +\infty)$$
2. 用于产生高斯分布的 $$\beta$$ 或 $$\sigma$$ 参数， $$\beta = \frac{1}{\sigma^2}$$
3. 是 $$x_+ = max(0, x)$$ 函数是平滑形式

有用性质：

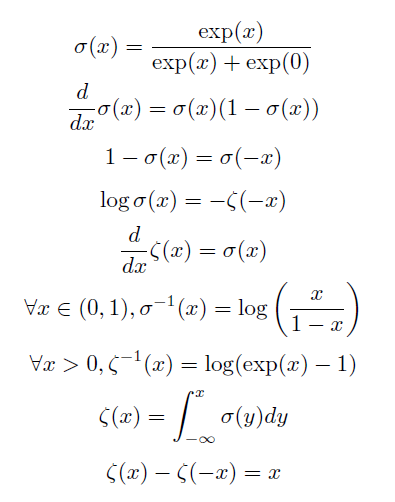
径向基函数 Radial Basis Function

将一个点到另一个点的距离映射成一个实值的函数。
这里面有三个未知：
（1）另一个点是什么点？默认是原点，也可以是指定点p。
（2）距离是什么距离？一般都使用欧氏距离
（3）对距离做怎样的操作？不同的RBF只要是这一点的不同。

欧氏径向基

距离为欧氏距离：
$$\begin{aligned} r(x) = ||x||_2 \ r(x, p) = ||x-p||_2 \end{aligned}$$

操作为线性操作：
$$\phi(r) = r$$

高斯径向基

距离为欧氏距离
操作为高斯函数：
$$\phi(r) = \exp(-\frac{r^2}{2\sigma^2})$$