2D仿射变换(2D Affine Transformation)

平移

我们先看平移变换：

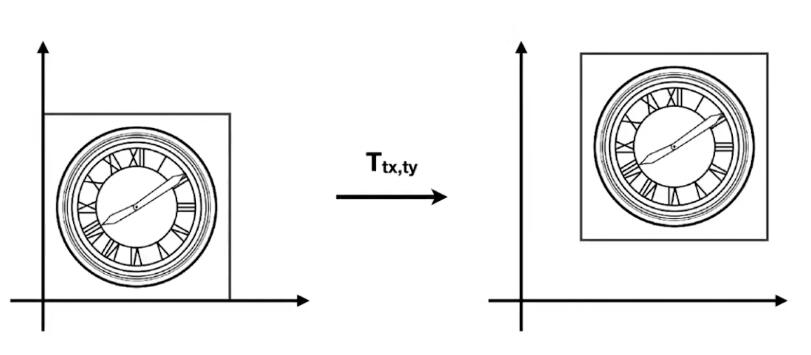
平移变换非常简单，可以由下面的式子表示：

$$x'=x+t_x\\ y'=y+t_y$$

但是有一个问题，我们不能把上述式子直接用矩阵的形式表达，需要在矩阵运算后再加一个偏移量：

$$\left[ \begin{array}{c} x'\\ y'\\ \end{array} \right] =\left[ \begin{matrix} a& b\\ c& d\\ \end{matrix} \right] \left[ \begin{array}{c} x\\ y\\ \end{array} \right] +\left[ \begin{array}{c} t_x\\ t_y\\ \end{array} \right]$$

📌如果只有平移，则 $a,b,c,d$ 构成一个单位矩阵

💡思考： 平移不是线性变换，不满足$X'=MX$

齐次坐标

为了解决“平移变换不能够线性变换表示”的问题，将坐标或向量添加一项(以2D为例)：

• 2D point = $(x, y, 1)^T$
• 2D vector = $(x, y, 0)^T$

这样，就可以用统一的X'=MX形式兼容线性变换和平移变换了：

$$\left( \begin{array}{c} x'\\ y'\\ w'\\ \end{array} \right) =\left( \begin{matrix} 1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\\ \end{matrix} \right) \cdot \left( \begin{array}{c} x\\ y\\ 1\\ \end{array} \right) =\left( \begin{array}{c} x+t_x\\ y+t_y\\ 1\\ \end{array} \right)$$

💡 当前维度解决不了的问题，可以考虑升维解决。
📌 为point增加一项1，因为point移动后不再是原来的point。为vector添加一项0，是因为向量具有平移不变性，向量平移后仍然是原向量。

📌 $(x, y, w)^T$ 如果用于表达2D点，等同于$(\frac{x}{w}, \frac{y}{w}, 1)$

添加项是否存在，不影响point与vector之间运算的意义：

$$vector + vector = vector\\ point + vector = point\\ point - point = vector\\ point + point = 两点的中点（齐次坐标下）$$

齐次坐标的性质：

• 有 $(x, y, z, 1)$ 这样一个坐标，那么为该坐标乘以一个不为0的数 $k$，即 $(kx, ky, kz, k)$，结果不变。
• 同理，给该坐标乘以坐标本身的 $z$ 值，它仍然表示着3D中的相同点。即 $(xz, yz, z^2, z)$，结果不变。
• 例如： $(1, 0, 0, 1)$ 和 $(2, 0, 0, 2)$ 都表示 $(1, 0, 0)$

仿射变换(Affine transformation)

线性变换 + 平移 = 仿射变换
所有的仿射变换，可以以齐次坐标的形式表达：

$$\left[ \begin{array}{c} X'\\ 1\\ \end{array} \right] =\left[ \begin{matrix} SR& T\\ 0& 1\\ \end{matrix} \right] \left[ \begin{array}{c} X\\ 1\\ \end{array} \right]$$

本文出自CaterpillarStudyGroup，转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES101_mdbook/