mathematics_basic_for_ML

Ordinary Differential Equation (ODE):

$$\frac{d\mathbf{x} }{dt} =\mathbf{f} (\mathbf{x},t) \quad \mathrm{or} \quad d\mathbf{x} =\mathbf{f} (\mathbf{x} ,t)dt$$

✅ 图中描述了一个 function，这个函数没有闭式解，而是 $\mathbf{x}$ 随着时间的变化。
✅ $f(\mathbf{x},t)$ 描述的是一个随时间变化的场 $f(\mathbf{x},t)$ 可以是一个用网络拟合的结果。

Analytical Solution:

$$\mathbf{x} (t)=\mathbf{x} (0)+\int_{0}^{t} \mathbf{f} (\mathbf{x} ,\tau )d\tau$$

✅ 这个积分经常无法计算，因此把离散化。

Iterative Numerical Solution:

$$\mathbf{x} (t+\Delta t)\approx \mathbf{x} (t)+\mathbf{f} (\mathbf{x} (t),t)\Delta t$$

Stochastic Differential Equation (SDE):

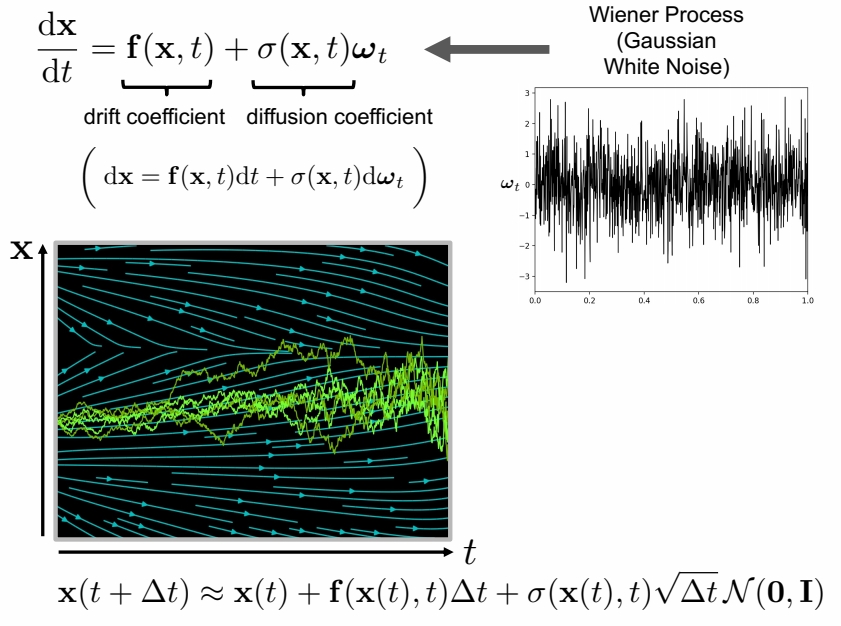
✅ $\sigma$ 描述 noise 的 scale。$\omega _ t$ 描述噪声。
✅ SDE 在每个时间步注入高斯白噪声。因此多次求解 $\mathbf{x}(t)$ 的结果是不一样的。