FinePhys: Fine-grained Human Action Generation by Explicitly Incorporating Physical Laws for Effective Skeletal Guidance
研究背景与问题
目的
合成物理合理的人类动作的视频
现有方法及局限性
在细粒度语义建模和复杂时间动态建模方面(例如生成像"转体0.5周的切换跳跃"这样的体操动作)往往产生不理想的结果。
本文方法
提出了FinePhys——一个结合物理原理的细粒度人类动作生成框架,通过有效的骨骼指导实现动作生成。具体而言:
- FinePhys首先以在线方式估计2D姿态,然后通过上下文学习进行2D到3D的维度提升。
- 为了缓解纯数据驱动3D姿态的不稳定性和有限可解释性,引入了一个由欧拉-拉格朗日方程控制的基于物理的运动重估计模块,通过双向时间更新计算关节加速度。
- 将物理预测的3D姿态与数据驱动姿态融合,为扩散过程提供多尺度2D热图指导。
在FineGym的三个细粒度动作子集(FX-JUMP、FX-TURN和FX-SALTO)上的评估表明,FinePhys显著优于竞争基线。全面的定性结果进一步证明了FinePhys生成更自然、更合理的细粒度人类动作的能力。
核心贡献
- 提出FinePhys框架:
一种面向细粒度人类动作视频生成的新方法,利用骨骼数据作为结构先验,并通过专用网络模块显式编码拉格朗日力学;
- 多维度物理约束融合
关键问题在于如何将物理规律连贯地融入学习过程。传统策略有三种:观测偏置(通过数据)、归纳偏置(通过网络)和学习偏置(通过损失)。FinePhys通过全维度整合物理约束: ❶ 观测偏置:引入姿态作为额外模态编码生物物理布局,利用上下文学习进行2D→3D提升,使用现有数据集中的平均3D姿态作为伪3D参考; ❷ 归纳偏置:通过全可微分神经网络模块实例化拉格朗日刚体动力学,其输出为欧拉-拉格朗日方程参数; ❸ 学习偏置:设计符合底层物理过程的损失函数。
- 实验验证优势
在细粒度动作子集上的大量实验表明,FinePhys显著优于各类基线模型,能生成更自然且物理合理的结果。
物理建模方法对比
| 方法 | 技术特征 | 局限性 | FinePhys突破 |
|---|---|---|---|
| 物理引擎派 (PhysGen/PhysDiff) | 依赖刚体仿真生成物理合理轨迹 | 计算成本高、无法处理细粒度关节运动 | 通过可微分PhysNet替代仿真器,实现端到端优化 |
| 方程嵌入派 (PIMNet/PhysPT) | 将物理方程作为损失函数约束 | 隐式约束易被生成模型忽略 | 显式参数化EL方程,直接输出动力学参数 |
| 数据驱动派 (PhysMoP) | 基于历史姿态预测未来状态 | 仅完成简单运动外推 | 处理模态转换(视频→3D姿态)、维度提升、内容生成三重挑战 |
主要方法
输入
- 视频输入:\(V_{in} = {f_i}_{i=1}^T\),从完整视频中采样的$T$帧;
推理阶段可以直接输入2D骨骼代替视频输入
- 文本描述:细粒度类别标签\(c\)的扩展描述(如"转体一周的切换跳跃"),通过文本扩展器\(\mathcal{E}\)(本文使用GPT-4[1])增强可理解性[73];
Pipeline
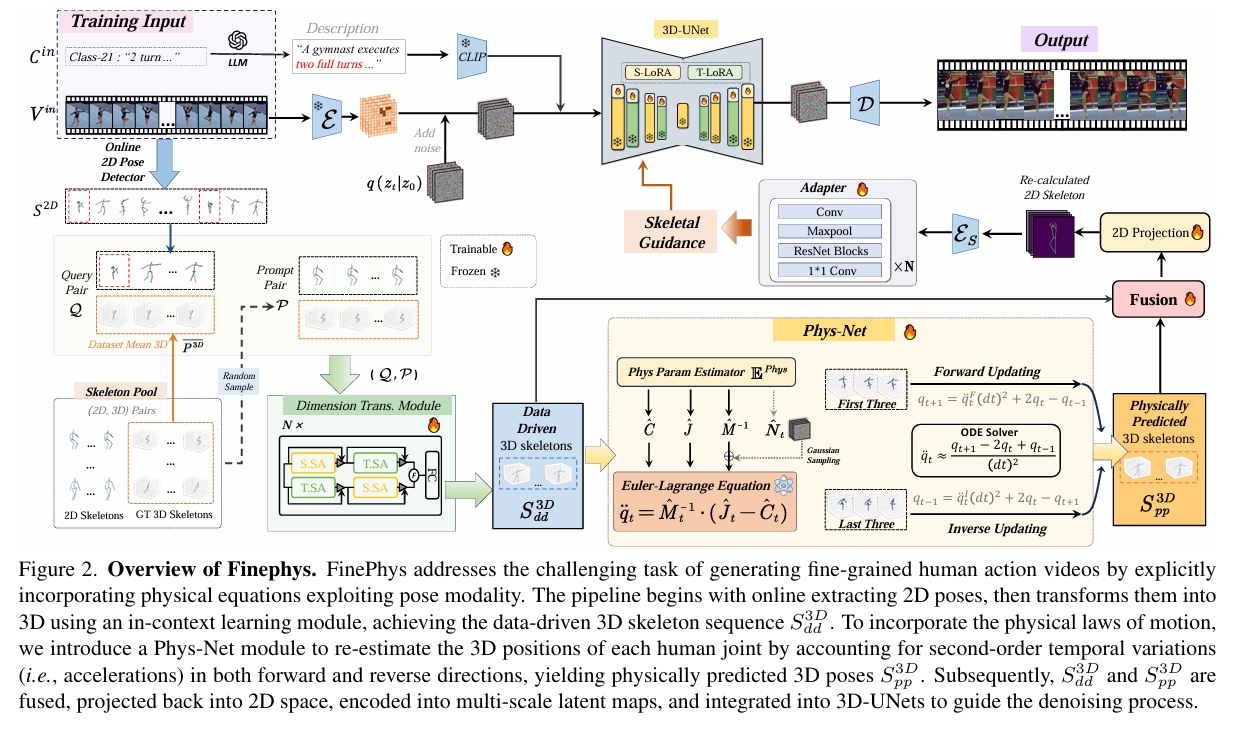
视频输入 → 2D姿态 → 3D姿态 → PhysNet优化 → 热图编码 → LDM条件
- 在线2D姿态估计:输入视频帧生成2D骨骼序列\(S_{2D} \in \mathbb{R}^{T \times J \times 2}\)(\(J\)为关节数),提供紧凑的生物力学结构表示;
- 上下文学习维度提升:将2D姿态通过上下文学习转换为数据驱动的3D骨骼序列\(S_{3D}^{dd} \in \mathbb{R}^{T \times J \times 3}\);
- 物理优化模块PhysNet:基于欧拉-拉格朗日方程计算双向二阶时序变化(加速度),重新估计3D运动动力学,生成物理预测的3D骨骼序列\(S_{3D}^{pp} \in \mathbb{R}^{T \times J \times 3}\);
- 多模态融合与投影:融合\(S_{3D}^{dd}\)与\(S_{3D}^{pp}\),投影回2D生成多尺度潜在热图;
- 引导生成:热图集成至3D-UNet各阶段,指导扩散去噪过程。
FinePhys:物理规律融合
观测先验:2D→3D维度提升
如图2左下所示:从真实数据集中获得2D-3D pair的先验,使用双流Transformer实现2D->3D lifting。
归纳偏置:物理感知模块
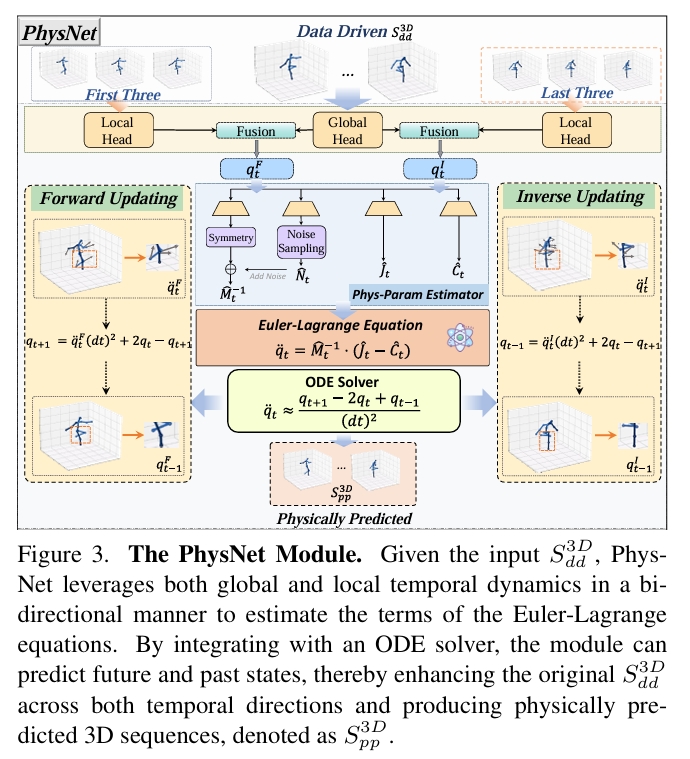
- 对2D→3D维度提升输出的3D序列进行编码,
$$
\begin{aligned}
q^{(g)} _ t &= E _ \theta^{(g)} \left( { S^{3D} _ {dd}(t) }_ {t=1}^T \right) \quad \in \mathbb{R}^{T \times (J \times 3)}, \\
q^{(l)(\rightarrow)} _ t &= E _ \theta^ {(l)} \left( { S ^ {3D} _ {dd}(t-2), S^{3D} _ {dd}(t-1), S^{3D} _ {dd}(t) } \right), \\
q^{(l)(\leftarrow)} _ t &= E _ \theta^{(l)} \left( { S^{3D} _ {dd}(t), S^{3D} _ {dd}(t-1), S^{3D} _ {dd}(t-2) } \right),
\end{aligned} \tag{8}
$$
其中\(q^{(l)(\rightarrow)}_t\)和\(q^{(l)(\leftarrow)}_t\)分别表示前向与反向时序编码。所有计算均双向进行——前向更新从前三帧开始,反向更新从后三帧开始。
-
取\(q^{(g)} _ t\) 和 \(q ^ {(l)( \rightarrow)} _ t \),使用下文补充部分的全身人体运动学模型,预测出\(\hat{q}_{t+1}^{(\rightarrow)}\)
-
取\(q^{(g)}_ t\)和\(q^{(l)(\leftarrow)} _ t\),使用下文补充部分的全身人体运动学模型,预测出\(\hat{q}_{t+1}^{(\leftarrow)}\)
-
双向估计平均:
$$
\hat{q} _ {t+1} = \frac{1}{2} \left( \hat{q} _ {t+1}^{(\rightarrow)} + \hat{q} _ {t+1}^{(\leftarrow)} \right)
$$
- 最终输出物理优化的3D骨骼序列:
$$
S^{3D} _ {pp} = E ^ {\text{pose}}(\hat{q}) \quad \in \mathbb{R} ^ {T \times 17 \times 3} \tag{18}
$$
学习偏置:优化目标
| 阶段 | 数据 | 关键约束 | 物理意义 |
|---|---|---|---|
| 预训练 | 含3D标注数据 | \(\mathcal{L}_ {3D}\) + \(\mathcal{L}_{noise}\) | 确保PhysNet初始参数满足刚体动力学 |
| 微调 | FineGym视频 | \(\mathcal{L}_{2D}\) | 适应真实场景的2D观测噪声与遮挡 |
| 生成 | 视频-文本对 | \(\mathcal{L}_ {\text{spat}} + \mathcal{L}_ {\text{temp}} + \mathcal{L}_ {\text{ad-temp}}\) | 平衡生成结果的视觉质量与运动连贯性 |
- 使用含真实3D姿态的大规模数据集
$$
\mathcal{L} _ {3D} = \sum _ {t=1}^T \sum _ {j=1}^J ||\hat{S}^{3D} _ {t,j} - S^{3D}_{t,j}||_2^2
$$
- 防止过度依赖对称性假设,允许微小非对称性(如单侧发力)
$$ \mathcal{L} _ {noise} = \sum _ {t=1}^T ||\hat{N} _ t|| _ F $$
- 2D投影损失,利用2D姿态估计结果作为弱监督信号
$$
\mathcal{L} _ {2D} = \sum _ {t=1}^T \sum _ {j=1}^J ||\mathcal{P}(\hat{S} ^ {3D} _ {t,j}) - S ^ {2D} _ {t,j}|| _ 2^2 + \mathcal{L} _ {noise} \tag{20}
$$
-
空间损失:单帧去噪误差
$$
\mathcal{L} _ {\text{spat}} = \mathbb{E} _ {z _ 0, c, \epsilon, t, i\sim \mathcal{U}(1,T)} \left[ ||\epsilon - \epsilon_\theta(z _ {t,i}, t, \tau _ \theta(c))|| _ 2^2 \right]
$$ -
时序损失:全局序列去噪误差
$$
\mathcal{L} _ {\text{temp}} = \mathbb{E} _ {z _ 0, c, \epsilon, t} \left[ ||\epsilon - \epsilon _ \theta( z _ t, t, \tau _ \theta(c))|| _ 2^2 \right]
$$
- 去偏时序损失:特征空间对齐误差(\(\phi\)为去偏算子[88])
$$
\mathcal{L} _ {\text{ad-temp}} = \mathbb{E} _ {z _ 0, c, \epsilon, t} \left[ ||\phi(\epsilon) - \phi(\epsilon_\theta(z _ t, t, \tau_\theta(c)))|| _ 2^2 \right]
$$
其中\(\phi\)是一种去偏运算,参考MotionDirector。
训练
数据集
| 数据集类型 | 构成与特点 | 作用 |
|---|---|---|
| 预训练数据集 | ||
| HumanArt [33] | 大规模骨骼-图像配对数据 | 训练骨骼热图编码器,建立视觉-骨骼跨模态关联 |
| Human3.6M [32] | 实验室环境多视角动捕数据(15种动作) | 提供高精度3D姿态真值,训练2D→3D模块 |
| AMASS [70] | 整合多个动捕数据集(SMPL模型参数) | 增强3D运动多样性,覆盖复杂人体变形 |
| FineGym子集 | FX-JUMP/TURN/SALTO(体操地板动作) | 验证细粒度动作生成能力,测试物理合理性 |
| FX-JUMP | 连续跳跃(如分腿跳) | 腾空阶段质心抛物线轨迹合理性 |
| FX-TURN | 快速转体(如单足旋转) | 角动量守恒与肢体收缩扩张关系 |
| FX-SALTO | 空翻(如后空翻两周) | 刚体动力学与柔体变形的耦合建模 |
Base Model
Stable Diffusion v1.5
AnimateDiff
实验
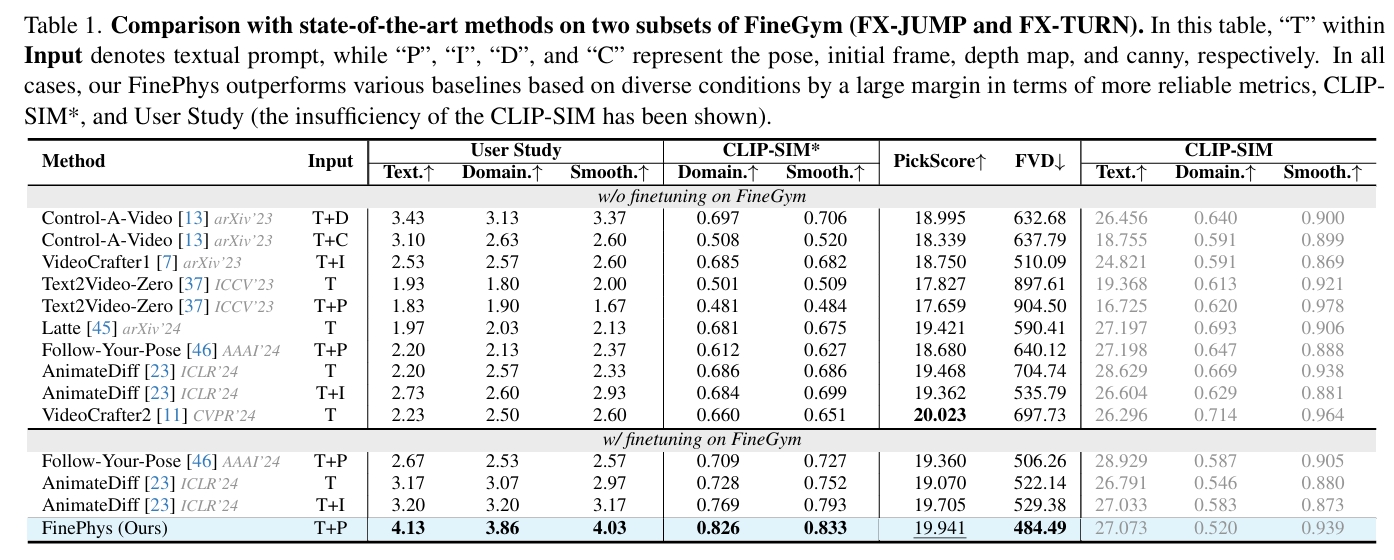
结论:
- 本文方向的生成质量和一致性都SOTA
- 其它方向结合了本文的FinePhys模块,也能有提升
在2D pose驱动的视频生成任务上,Follow Your Pose使用Cross Attention注入,本文使用Adapter注入。这两种都是有效且常用的注入方式,作者没有对这方面的控制效果做对比。
本文的主要贡献在于可微的3D动作物理合理性优化,可用于端到端的动作驱动任务的优化过程中。但是端到端的测试结果物理合理性优化在最终的视频生成中起到的作用,因为基于大量数据预训练的视频生成基模型所生成的视频本身就比较符合物理了。如果能跟HPE类的工作做对比,可能可以比较好地说明本文工作的效果。
在复杂动作上生成效果效果优于其它工作,可能是因为它使用了特定的数据集finetune,而其它工作是用于更通用的场景,没有使用有针对性的数据集。
AnimateDiff不是一个pose驱动的模型,不知道是怎么参与对比的?
补充
全身人体运动学模型
欧拉公式可转换为:
$$
M(q)\ddot{q} = J(q, \dot{q}) - C(q, \dot{q}), \tag{3}
$$
其中\(\dot{q}\)和\(\ddot{q}\)分别表示关节速度与加速度。
| 项 | 物理含义 | 人体运动对应实例 |
|---|---|---|
| \(M(q)\ddot{q}\) | 惯性力 | 空翻时身体各部位抵抗加速度变化的力 |
| \(J(q, \dot{q})\) | 外部驱动力 | 肌肉发力、重力、地面反作用力 |
| \(C(q, \dot{q})\) | 约束力 | 膝关节不可过度伸展的解剖限制 |
使用网络模型预测出M、C、J,公式3的离散化实现:
$$
\ddot{q} _ t = \hat{M}^{-1}(q _ t) \cdot [\hat{J}(q _ t, \dot{q}_t) - \hat{C}(q _ t, \dot{q} _ t)]
$$
通过中心差分公式更新关节位置:
$$
q _ {t+1} = \ddot{q} _ t \Delta t^2 + 2q _ t - q _ {t-1}
$$
$$ \begin{align*} q_{t+1} & = q_t+v_t\cdot \Delta t\\ & = q_t+(v_{t-1}+a_t\cdot \Delta t)\cdot \Delta t\\ & = q_t+v_{t-1}\cdot \Delta t+a_t\cdot (\Delta t)^2\\ & = q_t+(q_t-q_{t-1})+a_t\cdot (\Delta t)^2\\ & = a_t\cdot (\Delta t)^2+2q_t-q_{t-1} \end{align*} $$
Reference
分段刚体的刚体动力学:https://caterpillarstudygroup.github.io/GAMES105_mdbook/Simulation.html