Particle-Grid Neural Dynamics for Learning Deformable Object Models from RGB-D Videos
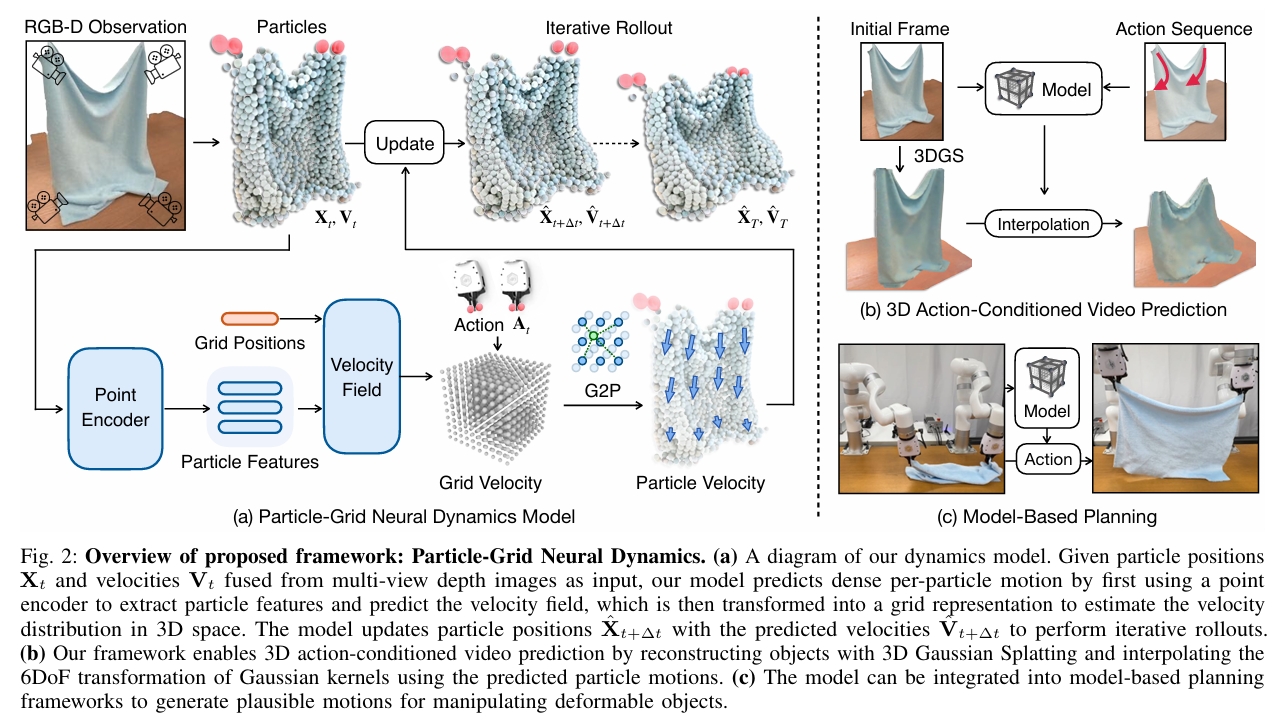
由于可变形物体多样的物理特性以及难以从有限的视觉信息中估计其状态,建模其动力学具有挑战性。我们通过一个神经动力学框架来解决这些挑战,该框架在混合表示中结合了物体粒子 (object particles) 和空间网格 (spatial grids)。我们的粒子-网格模型 (particle-grid model) 既能捕捉全局形状和运动信息,又能预测密集的粒子运动,从而能够建模具有不同形状和材料的物体。粒子代表物体形状,而空间网格则将三维空间离散化,以确保空间连续性并提高学习效率。结合用于视觉渲染的高斯泼溅 (Gaussian Splatting) 技术,我们的框架实现了完全基于学习的可变形物体数字孪生模型 (fully learning-based digital twin),并生成动作条件的三维视频 (3D action-conditioned videos)。
通过实验,我们证明了我们的模型能够从机器人-物体交互的稀疏视角RGB-D记录 (sparse-view RGB-D recordings) 中学习各种物体(如绳索、布料、毛绒玩具和纸袋)的动力学,同时还能在类别层面 (category level) 上泛化到未见过的实例。我们的方法优于最先进的基于学习的模拟器 (learning-based simulators) 和基于物理的模拟器 (physics-based simulators),尤其是在相机视角有限 (limited camera views) 的场景下。此外,我们展示了所学模型在基于模型的规划 (model-based planning) 中的实用性,使其能够在一系列任务中实现目标条件的物体操作 (goal-conditioned object manipulation)。
项目页面位于:https://kywind.github.io/pgnd
研究背景与问题
任务
输入:3DGS场景的静态模型、交互操作
输出:预测GS球未来运动
主要方法
本文中仿真全过程使用的粒子是点云粒子。GS球只是最后渲染使用。
粒子-网格神经动力学
状态表示
| 符号 | 维度 | 含义 |
|---|---|---|
| Xt | 3*n | t时刻每个球的位置 |
| Vt | 3*n | t时刻每个球的速度 |
控制表示
\(A_t\) 表示机器人在时刻 \(t\) 对物体施加的外部作用。
$$ A_t = (y, T_t, \dot{T}_t, o_t), $$
| 符号 | 维度 | 含义 |
|---|---|---|
| \(y\) | 动作类型标签,是一个二元标签,用于指示动作是抓取操作还是非抓取式交互 | |
| \(T_t\) | 为末端执行器位姿 | |
| \(\dot{T}_t\) | 为其时间导数 | |
| \(o_t\) | 夹爪张开距离 |
动力学函数
$$ V_{t+1} = f_\theta(X_{(t-h):t}, V_{(t-h):t}, A_t) \\ X_{t+1} = X_t + V_{t+1} $$
粒子-网格模型
**使用端到端神经网络学习神经动力学参数 θ 通常会导致累积误差,进而引发预测不稳定。**因此同样采用particle-grid表示,以融入与空间连续性及局部信息集成相关的归纳偏置。
定义一个均匀分布的网格:
$$ G_{l_x, l_y, l_z, \delta} = { (k_x \delta, k_y \delta, k_z \delta) \mid k_i \in [l_i], \forall i \in {x, y, z} }. $$
末端执行器及每个粒子必定属于某个网格。
Grid用于学习上文提到的\(f_\theta\)函数。具体包含以下模块:
- \(f^{feature}_\phi\) 是基于神经网络的点编码器,用于从输入粒子中提取特征(第 III-B1 节);
- \(f^{field}_\psi\) 是基于神经网络的函数,用于根据提取的特征参数化神经速度场(第 III-B2 节);
- \(g^{grid}\) 是网格速度编辑控制方法,用于编码碰撞表面和机器人夹爪的运动(第 III-B4 节);
- \(h^{G2P}\) 是网格到粒子的积分函数,用于从基于网格的速度场计算粒子速度(第 III-B3 节)。
基于网格来学习速度场比直接学习每个粒子的速度更稳定。
网格模块
点编码器
输入:粒子位置与速度
输出:粒子的潜在特征
$$ Z_t = f^{feature}\phi (X{(t-h):t}, V_{(t-h):t}). $$
模型结构: PointNet
特征编码器必须提取对遮挡鲁棒的特征,以供后续速度解码使用。
神经速度场
输入:网格点g的位置x、网格点g的部感知特征z
输出:网格点g的速度向量
$$ \hat{v}{g,t} = f^{field}\psi (\gamma(x_g), z_{g,t}), $$
其中 \(\gamma\) 为正弦位置编码,局部感知特征 \(z_{g,t}\) 定义为网格位置邻域内粒子特征的平均池化:
$$ z_{g,t} = \frac{\sum_{p \in N_r(X_t, x_g)} z_{p,t}}{|N_r(X_t, x_g)|}, $$
半径 \(r\) 是一个超参数 (r),用于控制一个网格点所关注的粒子特征数量,从而促使网络预测依赖于局部几何的速度。
网格到粒子速度传递
遵循物质点法(MPM)的思路,采用连续的B样条核函数将网格速度 (\hat{v}{g,t}) 传递至粒子速度 (\hat{v}{p,t}):
$$ \hat{v}{p,t} = \sum{g \in G} \hat{v}{g,t} w{pg,t}, $$
预测值 \(\hat{V} \in \mathbb{R}^{3 \times n}\) 作为动力学函数 \(f_\theta\) 的最终输出,并用于更新粒子的位置。
变形控制
通过与外部物体交互来控制变形
网格速度编辑GVE
改变网格上的速度以匹配物理约束:
- 对于地面接触从接触面回推速度并加入摩擦项
- 定义刚性抓取点的运动,计算抓取中心点 \(x_{grasp,t}\) 附近的点,按如下方式修改其速度:
$$ v_{g,t} = \omega_t \times (x_g - x_{grasp,t}) + \dot{x}_{grasp,t}, $$
其中 \(\omega_t\) 和 \(\dot{x}{grasp,t}\) 分别为时刻 \(t\) 时夹爪的角速度和线速度,\(x_g\) 和 \(v{g,t}\) 分别为网格点 \(g\) 的位置和速度。
机器人粒子法
用于非抓取式动作建模,例如推动箱子。
用携带夹爪动作信息的额外粒子表示机器人夹爪,并将其融合到物体点云中
并在增广后的点云上建模粒子-网格动力学函数。
这便将动作信息注入粒子特征中,但不会显式强制粒子按指定速度运动,从而支持非抓取式操控。
数据收集与训练
数据收集
- 通过真实交互记录多视角的RGB-D视频,捕捉机器人-物体的随机交互过程。
- 用Segment-Anything [18, 39] 提取视频中物体的持续掩码。
- 将分割出的物体进行裁剪,并使用CoTracker [15] 对其进行跨帧跟踪,从而得到2D轨迹。
- 借助深度信息,通过逆投影将这些2D速度映射至3D空间,生成具有持续粒子跟踪信息的多视角融合点云。
训练
损失函数定义为预测粒子位置与实际粒子位置之间的均方误差位置。
渲染与动作条件视频预测
首先对点云集合 \(X\) 应用动力学模型,得到下一帧的预测 \(\hat{X}\)。点集 \(\hat{X}\) 可以来自对 \(X_{GS}\) 的采样,或从与 \(X_{GS}\) 处于同一坐标系内的额外点云观测中获取。
将 \(X\) 视为控制点,并对其预测运动进行插值,从而更新 \(X_{GS}\) 和 \(R_{GS}\),生成新的高斯中心与旋转。
假设高斯泼溅的颜色、尺度和不透明度保持不变。