SCORE-BASED GENERATIVE MODELING THROUGHSTOCHASTIC DIFFERENTIAL EQUATIONS
核心问题是什么?
一种从数据生成噪声的方法:通过缓慢注入噪声将复杂的数据分布平滑地转换为已知的先验分布
一种从噪声生成数据的方法:SDE 通过缓慢消除噪声将先验分布转换回数据分布。其中SDE 仅取决于扰动数据分布的时间相关梯度场(也称为分数)。
核心贡献是什么?
- 通过神经网络准确估计这些分数,并使用数值 SDE 求解器生成样本。
- 引入预测校正框架来纠正离散逆时 SDE 演化中的错误
- 导出等效的神经常微分方程,它从与 SDE 相同的分布中采样,但还可以进行精确的似然计算,并提高采样效率
- 提供了一种使用基于分数的模型解决逆问题的新方法
大致方法是什么?
Score function
生成模型的目标就是要得到数据的分布。现在我们有一个数据集,我们想要得到数据的概率分布p(x)。一般我们会把这个概率分布建模成这样:
$$ p_\theta(x) = \frac{e^{-f_\theta(x)}}{Z_\theta} $$
这里f(x)可以叫做unnormalized probabilistic model或者energy-based model。Z是归一化项保证p(x)是概率。\(\theta\)是他们的参数。 我们一般可以通过最大化log-likelihood的方式来训练参数\(\theta\)
$$ \max_\theta \sum_{i=1}^N \log p_\theta(x_i) $$
即让数据集里的数据(即真实数据分布的采样)log-likelihood最大。
但是因为Z是intractable的,我们无法求出\(\log p_\theta(x_i)\),自然也就无法优化参数。 为了解决归一化项无法计算的问题,我们引入score function。 score function的定义为
$$ s_\theta(x) = \nabla_x \log p_\theta(x) = -\nabla_x f_\theta(x) - \nabla_x \log z_\theta \\ = -\nabla_x f_\theta(x) $$
因此s(x)是一个与z无关的函数。
Score matching
现在我们想要训练一个网络来估计出真实的score function。自然地,我们可以最小化真实的score function \(\nabla_x \log p_\theta(x)\)和网络输出的MSE\(s_\theta(x)\)。 但是这样的一个loss我们是算不出来的,因为我们并不知道真实的p(x)是什么。而score matching方法就可以让我们在不知道真实的的情况下最小化这个loss。Score matching的推导如下:

Score Matching Langevin Dynamics (SMLD)
现在我们已经通过神经网络学习到了数据分布的score function,那么如何用score function从这个数据分布中得到样本呢?答案就是朗之万动力学采样(Langevin Dynamics):
$$ x_{i+1} = x_i + \epsilon \nabla_x \log p(x) + \sqrt {2 \epsilon} z_i, z_i \in N(0, I), i = 0, 1, \dots, K $$
这里的采样是一个迭代的过程。\(\epsilon\)是一个很小的量。x0随机初始,通过上面的迭代式更新。当迭代次数K足够大的时候,x就收敛于该分布的一个样本。
这样我们其实就得到了一个生成模型。我们可以先训练一个网络用来估计score function,然后用Langevin Dynamics和网络估计的score function采样,就可以得到原分布的样本。因为整个方法由score matching和Langevin Dynamics两部分组成,所以叫SMLD。
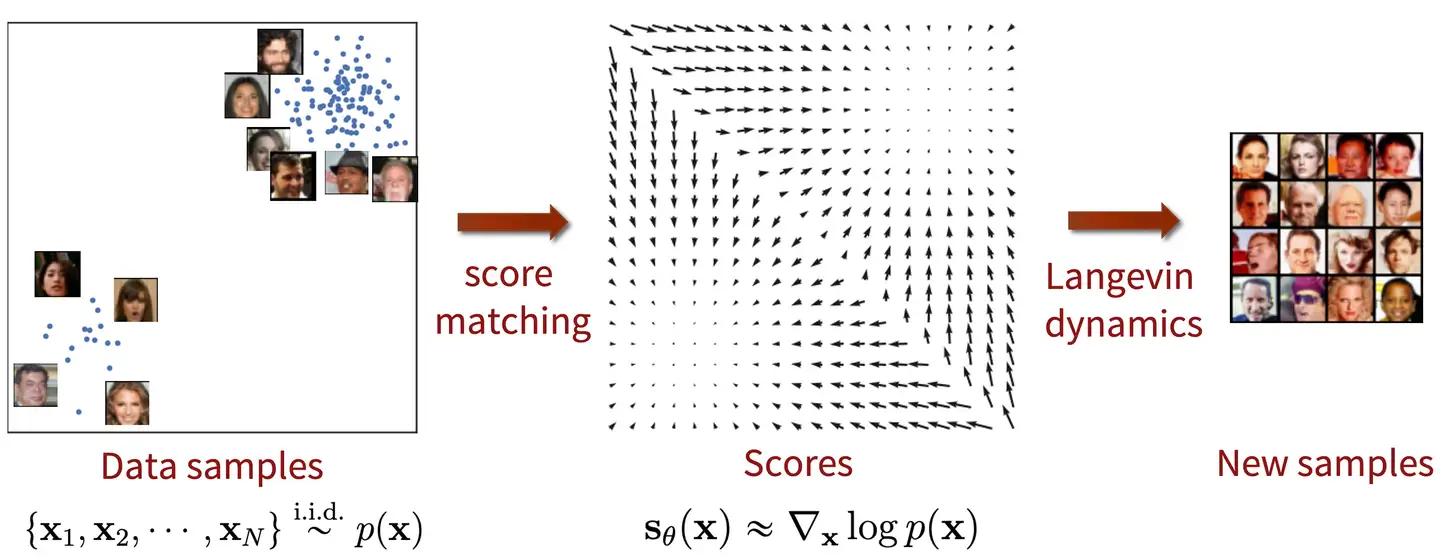
Pitfall
现在我们得到了SMLD生成模型,但实际上这个模型由很大的问题。
$$ L = \int p(x) ||\nabla_x \log p(x) - s_\theta(x)||^2 dx $$
观察我们用来训练神经网络的损失函数,我们可以发现这个L2项其实是被p(x)加权了。所以对于低概率的区域,估计出来的score function就很不准确。如果我们采样的初始点在低概率区域的话,因为估计出的score function不准确,很有可能生成不出真实分布的样本。
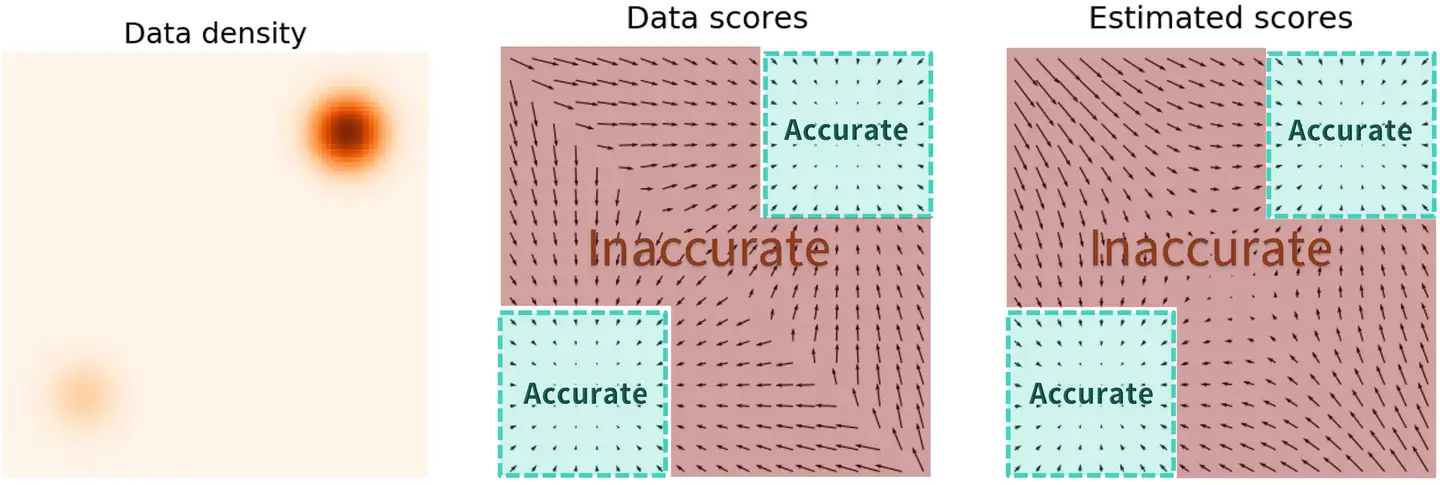
Fix it with multiple noise perturbations
那怎么样才能解决上面的问题呢? 其实可以通过给数据增加噪声扰动的方式扩大高概率区域的面积。给原始分布加上高斯噪声,原始分布的方差会变大。这样相当于高概率区域的面积就增大了,更多区域的score function可以被准确地估计出来。
但是噪声扰动的强度如何控制是个问题:
- 强度太小起不到效果,高概率区域的面积还是太小
- 强度太大会破坏数据的原始分布,估计出来的score function就和原分布关系不大了
这里作者给出的解决方法是加不同程度的噪声,让网络可以学到加了不同噪声的原始分布的score function。
我们定义序列\(\sigma_i\)\(_{i=1}^L\),代表从小到大的噪声强度。这样我们可以定义经过噪声扰动之后的数据样本,服从一个经过噪声扰动之后的分布,
$$ x + \sigma_iz \in p_{\sigma_i}(x) = \int p(y)N(x|y, \sigma_i^2I)dy $$
我们用神经网络来估计经过噪声扰动过的分布的score function。采样方式也要做出相应的变化,我们对于不同的噪声强度L做Langevin采样,上一个scale的结果作为这一次的初始化。这种采样方式也叫做Annealed Langevin dynamics,伪代码如下图所示。

有效
缺陷
验证
启发
Connection with DDPM
如果我们把SMLD和DDPM的优化目标都写出来的话可以发现他们的形式都是一样的。
遗留问题
参考材料
https://zhuanlan.zhihu.com/p/583666759