Consistency Models
https://arxiv.org/pdf/2303.01469.pdf
https://github.com/openai/consistency_models
https://readpaper.com/pdf-annotate/note?pdfId=4761865581863370753¬eId=2187834810264506624
核心问题是什么?
扩散模型在图像、音频和视频生成方面取得了重大突破,但它们依赖于迭代生成过程,导致采样速度较慢,限制了其实时应用的潜力。
现有的快速采样方法包括更快的数值ODE求解器和蒸馏技术。ODE求解器仍然需要超过10个评估步骤来生成有竞争力的样本。大多数蒸馏方法,依赖于在蒸馏之前从扩散模型中收集大量的样本数据集,这本身就是计算成本很高的。据我们所知,唯一不受这一缺点影响的蒸馏方法是渐进蒸馏(PD)。
核心贡献是什么?
- 一致性模型在设计上支持快速的一步生成,同时仍然允许少步采样以换取样本质量的计算。
- 一种新的生成模型家族,可以在没有对抗性训练的情况下实现高样本质量
- 支持zero-shot数据编辑,如图像修补、着色和超分辨率,而不需要对这些任务进行明确的训练。
- 一致性模型既可以作为提取预训练扩散模型的一种方式训练,也可以作为独立的生成模型训练。
大致方法是什么?
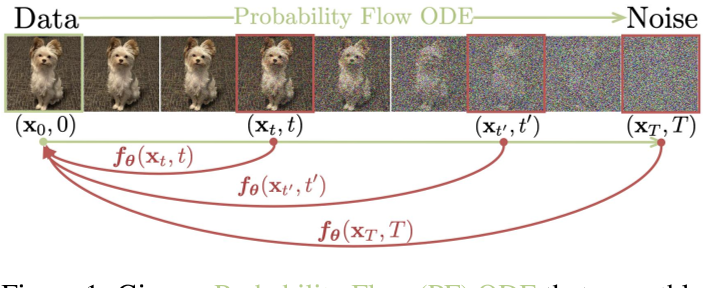
我们建立在连续时间扩散模型中的概率流(PF)常微分方程(ODE)之上(简单来说,就是图像前向传播的无参加噪过程),其轨迹平滑地将数据分布转换为可处理的噪声分布。而CM可将任何时间步骤的任何分布点映射到轨迹的起点。CM模型的一个显著特性是自一致性:同一轨迹上的点映射到相同的起始点。因此,我们把这样的模型称为一致性模型。
一致性模型的定义
假设存在一个函数f,对于同一条PF ODE轨迹上的任意点都有相同的输出:
$$ \boldsymbol{f} ( x_t , t ) = \boldsymbol{f} ( x_{t^{\prime}} , t^{\prime} ) \text { for all } t , t ^{\prime} \in [ \epsilon , T ] $$
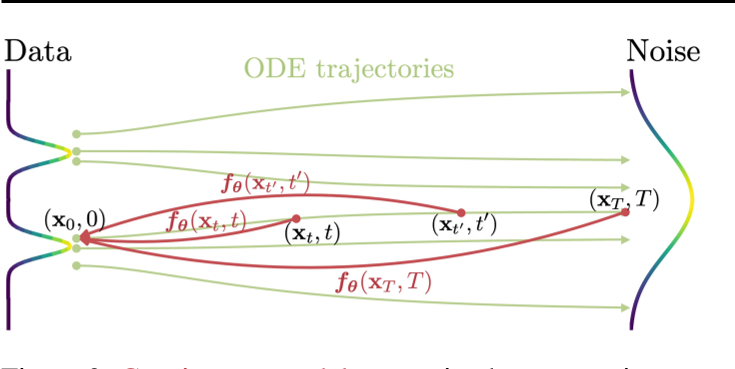
consistency model的目标是从数据中估计一致性函数f,来迫使self-consistency性质
一致性模型参数化
要拟合的一致性函数 \( f(\cdot, \cdot) \)要满足两个条件:①同一个轨迹上的点输出一致;②在起始点f为一个对于x的恒等函数
第一种做法简单地参数化consistency models
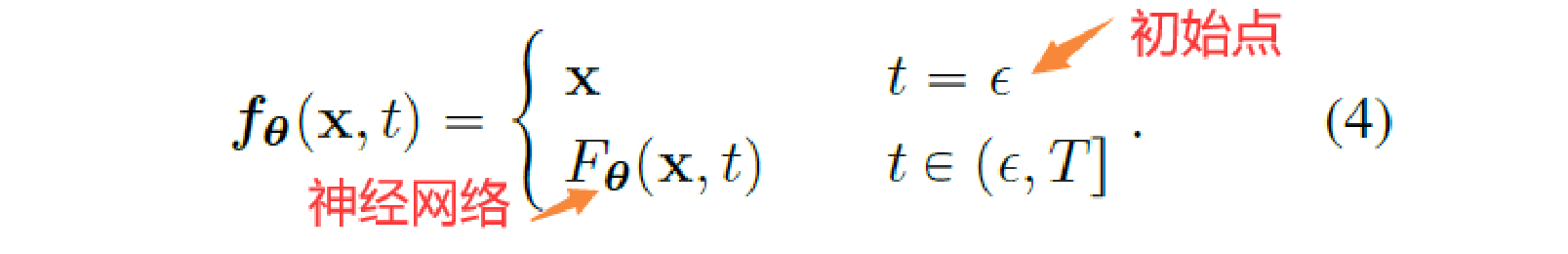
第二种做法使用跳跃连接(作者和许多其他的都用这个)

其中 \(c_{skip}\)和 \(c_{out}\)为可微函数,满足 \(c_{skip}(\epsilon) = 1, c_{out}(\epsilon) = 0\). \(F_{\theta}\)为深度神经网络,可使用一致性损失来学习,输出维度同 x.
一致性模型采样
观察 f 的性质,显然, \(f(x_T,T) = x_{\epsilon}\)可以得到我们想要的生成结果。但一般认为,这样的生成误差会比较大。所以我们每次从\(x_{\tau_n}\) 预测出初始的 \(x_\)后,回退一步来预测\(x_{\tau_{n-1}}\) 来减小误差。因此有如下多步采样的算法。
实际中,采用贪心算法来寻找时间点,通过三值搜索每次确定一个时间点。
Consistency Models 的训练方式
考虑到 Consistency Models 的性质,对采样轨迹上的不同点,f应该有一个相同的输出,自然我们需要找到采样的轨迹。
Training Consistency Models via Distillation
如果我们有预训练的diffusion model,自然可以构建轨迹。
假设采样轨迹的时间序列为
$$ t_{1}=\epsilon<t_{2}<\cdots<t_{N}=T $$
通过运行数值ODE求解器的一个离散化步骤从 \(\mathbf{x}{t{n+1}}\) 得到 \( \mathbf{x}{t{n}}\)
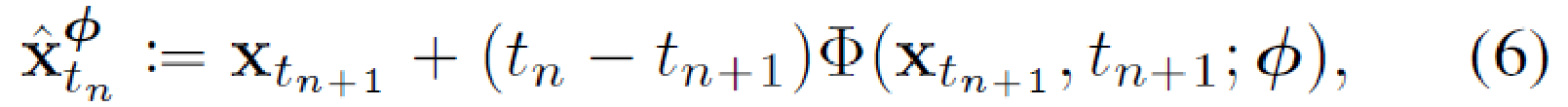
其中Φ(...;ϕ)为ODE solver,可以是任意ODE Solver,一般来说阶数越高的 Solver 求解精度越高。
例如使用Euler solver
$$ \frac{\mathrm{dx}}{\mathrm{d} t}=-t s_{\phi}\left(\mathrm{x}_{t}, t\right)\\ \Phi(\mathrm{x}, t ; \phi)=-t s _{\phi}(\mathrm{x}, t) $$
带入上式得到
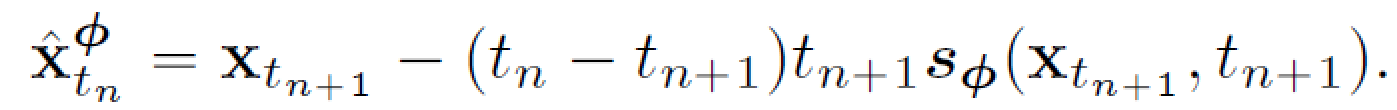
对于处于同一轨道的 \((x_{t_{n-1}},t_{n-1}),(\hat x_{t_{n}}^\phi,t_{n})\),f应该有相同的输出,我们用距离函数 d 来衡量输出是否相同。因而有如下训练损失
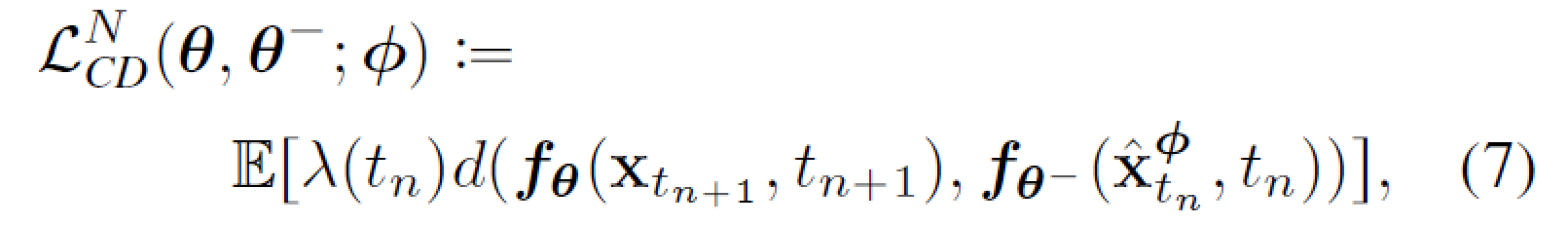
其中 \(\lambda\)用来对不同时间步赋予不同重要性,\(\theta^-\)为 EMA 版本的权重。采用EMA来更新模型会提高训练的稳定性,并且性能会更好。
综合上述过程,蒸馏(Consistency Distillation)的算法为

Training Consistency Models in Isolation
Consistency models也可以单独进行训练,而不依赖于预训练好的扩散模型。在蒸馏的过程中,我们实际上用预训练模型来估计得分\(\nabla \log p_t(x)\) 。 如果从头训练,需要找一个不依赖于预训练模型的估计方法。
作者在论文中证明了一种新得分函数的估计

利用该得分估计,作者为从 Isolation Training 构建了一个新的训练损失,
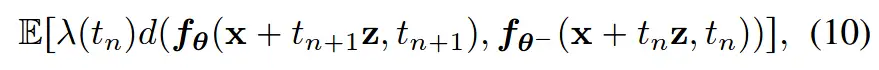
并且证明了该 Loss 和 Distillation Loss 在最大间隔趋于0时相等。即
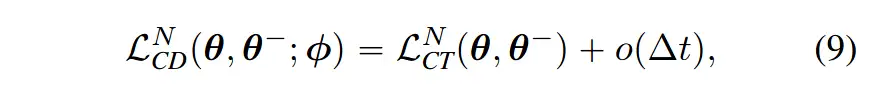
从而可以利用上述 loss 训练一个 Consistency Models,并且不依赖于已有 Diffusion Model。具体算法如下

有效
缺陷
验证
启发
遗留问题
参考材料
[1] https://zhuanlan.zhihu.com/p/621673283 [2] https://blog.csdn.net/singxsy/article/details/130243343 [3] https://blog.csdn.net/WiSirius/article/details/134670307 [4] https://www.jianshu.com/p/3b712cbe6d0d