Denoising Diffusion Implicit Models
核心问题是什么?
DDPM的生成速度太慢,其本质原因是:在对\(p_{\theta}(x_{t-1}|x_t)\)的推导中,DDPM用到了一阶马尔可夫假设,使得\(p(x_t|x_{t-1},x_0)=p(x_t|x_{t-1})\) 。
在DDPM中往往需要较大的T才能得到较好的结果(论文中 ),这导致需要T次采样步长。因此重建的步长非常长,导致速度慢。
核心贡献是什么?
DDPM为什么这么慢
DDPM速度慢的本质原因是对马尔可夫假设的依赖,导致重建需要较多的步长。那么不用一阶马尔可夫假设,有没有另一种方法推导出\(p(x_{t-1}|x_{t},x_0)\) 。
前面我们提到,DDPM的前向过程主要是用于构造数据集,来训练噪声预测模型。在实际优化过程中,其实并没有用到前向过程的马尔可夫假设,只用到了推理分布 \(q(x_t|x_0)\) ,因此如果DDIM也能满足这个推理分布的话,那么直接就可以复用DDPM的噪声预测模型了
✅ 马尔可夫假设认为,\(x_{t}\)只与\(x_{t-1}\)有关。但前向过程中\(x_{t}\)由\(x_0\)得到,而不是由\(x_{t-1}\)得到,因此不依赖马尔可夫假设。
✅ 而反向过程中,\(x_{t-1}\)需要\(x_{t}\),因此是依赖马尔可夫假设。
✅ 如果找到一种方法,不需要计算通过\(x_{t}\)的分布来计算\(x_{t-1}\)的分布,那么就是不依赖于马尔可夫假设。
DDIM如何不依赖马尔科夫假设
归纳一下DDIM想要做的
- DDIM希望构建一个采样分布\(p(x_{t-1}|x_{t},x_0)\),这个采样分布不依赖一阶马尔科夫假设
- DDIM希望维持这个前向推理分布\(q(x_t|x_0) = \mathcal{N} (x_t;\sqrt{{\alpha_t}}x_0,(1-{\alpha_t})I)\)
DDPM中的\(p(x_{t-1}|x_{t},x_0)\)
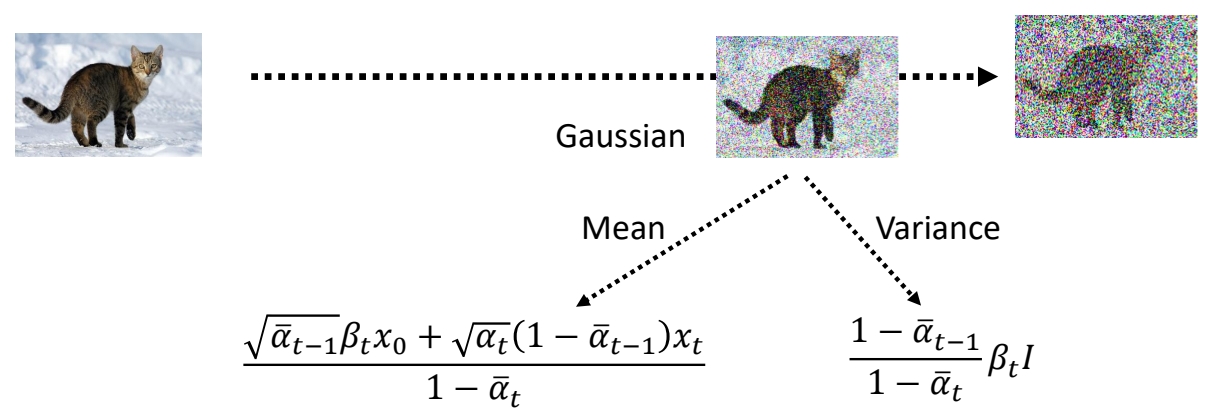
根据DDPM的结果参考,采样分布\(p(x_{t-1}|x_{t},x_0)\)是一个高斯分布,并且均值是\(x_{0}, x_t\)的线性函数,方差是一个与时间步有关的函数。
DDIM中的\(p(x_{t-1}|x_{t},x_0)\)
DDIM也假设\(p(x_{t-1}|x_{t},x_0)\)是一个高斯分布,并且均值也是\(x_{0}, x_t\)的线性函数,方差是时间步t的函数,即:
$$ p(x_{t-1}|x_{t},x_0) = \mathcal{N}(x_{t-1};\lambda x_0 + k x_t, \sigma^2_t I) $$
这个采样分布有3个自由变量\(\lambda, k, \sigma_t\),理论上有无穷多个解。但DDIM想要维持与DDPM一致的推理分布\(q(x_t|x_0) = \mathcal{N} (x_t;\sqrt{{\alpha_t}}x_0,(1-{\alpha_t})I)\) 。这样问题就转化成,找到一组解\(\lambda^{ * }, k^{ * }, \sigma_t^{ * }\) ,使得DDIM的推理分布满足\(q(x_t|x_0) = \mathcal{N} (x_t;\sqrt{{\alpha_t}}x_0,(1-{\alpha_t})I)\) 。
求解DDIM中的未知量
根据\(q(x_t|x_0)\)条件,列出方程组并求解未知量\(\lambda, k, \sigma_t\):
$$ p(x_{t-1}|x_{t},x_0) = \mathcal{N}(x_{t-1};\lambda x_0 + k x_t, \sigma^2_t I)\\ q(x_{t-1}|x_0) = \mathcal{N} (x_{t-1};\sqrt{{\alpha_{t-1}}}x_0,(1-{\alpha_{t-1}})I) $$
两个方程,三个未知量。因此把\(\sigma_t\)把看作是控制生成过程的超参,只解\(\lambda, k\)。
解方程过程省略,见参考材料[1]。解得:
DDIM采样分布的使用
解出(\lambda, k\),得到DDIM的采样分布:
不同的\(\sigma_t\)对应不同生成过程。由于前向过程没变,故可以直接用DDPM训练的噪声预测模型。其采样过程如下:
两个特殊的case
- 当 \(\sigma_t = \sqrt{\frac{1-\alpha_{t-1}}{1-\alpha_{t}}}\sqrt{\frac{1-\alpha_{t}}{\alpha_{t-1}}}\)时,此时的生成过程与DDPM一致。
- 当\(\sigma_t = 0\)时,此时采样过程中添加的随机噪声项为0,当给定初始噪声z时,采样过程是确定的,此时的生成模型是一个隐概率模型(implicit probabilstic model)[1]。作者将此时diffusion model称之为denoising diffusion implicit model(DDIM)。此时的采样递推公式
DDIM,快速地生成且生成结果是确定的。由于生成结果是确定的,可用于latent space插值、编辑等任务。
大致方法
DDIM加速采样的思路很简单,假定原本的生成序列为\(L=[T,T-1,\dots,1]\) ,其长度为\(\dim(L)=T\) ,我们可以从生成序列 中构建一个子序列\(\tau=[\tau_s,\tau_{s-1},\dots,\tau_1]\) ,其长度\(\dim(\tau)=S,S\ll T\) 。在生成过程,按照构造序列\(\tau\)进行采样。此时的采样递推序列为
DDPM vs DDIM
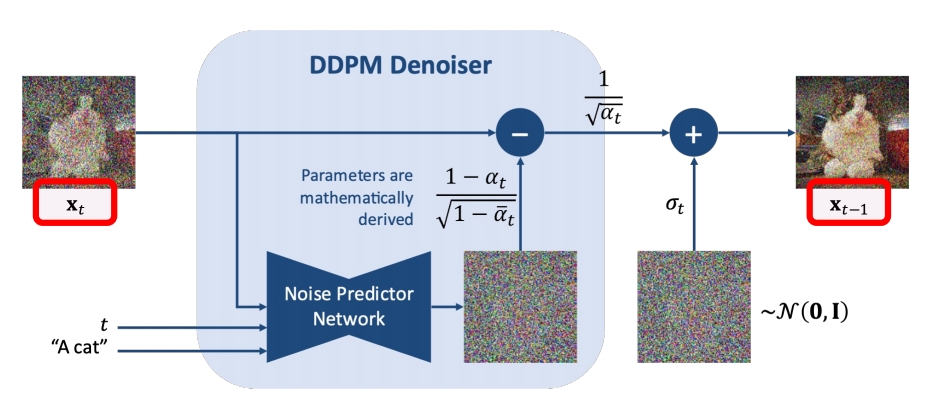 | DDPM cannot skip timesteps A few hundreds steps to generate an image |
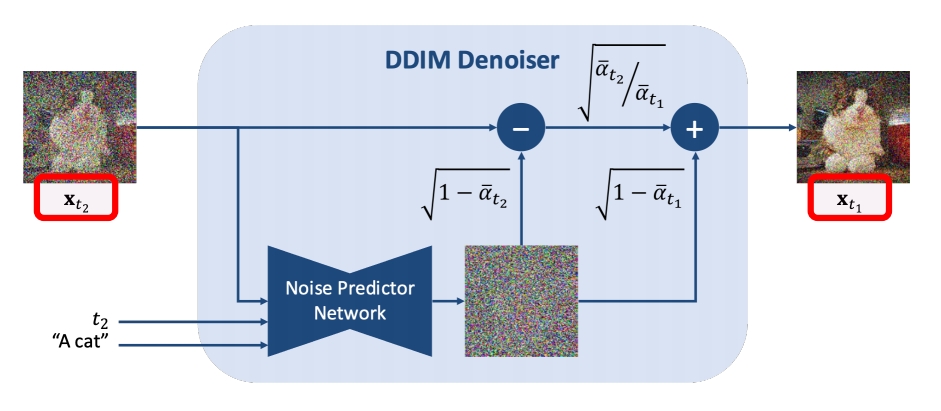 | DDIM can skip timesteps Say 50 steps to generate an image |
有效性
- 论文给出了不同的采样步长的生成效果。可以看到DDIM在较小采样步长时就能达到较好的生成效果。如CIFAR10 S=50就达到了S=1000的90%的效果,与之相对DDPM只能达到10%左右的FID效果。可见DDPM在推导采样分布中用了马尔可夫假设的确限制了它的采样间隔。
- DDIM将\(\sigma_t\) 设置为0,这让采样过程是确定的,只受\(x_T\)影响。作者发现,当给定\(x_T\) ,不同的的采样时间序列\(\tau\) 所生成图片都很相近,\(x_T\)似乎可以视作生成图片的隐编码信息。
启发
有个小trick
我们在实际的生成中可以先设置较小的采样步长进行生成,若生成的图片是我们想要的,则用较大的步长重新生成高质量的图片。
The task of Inversion
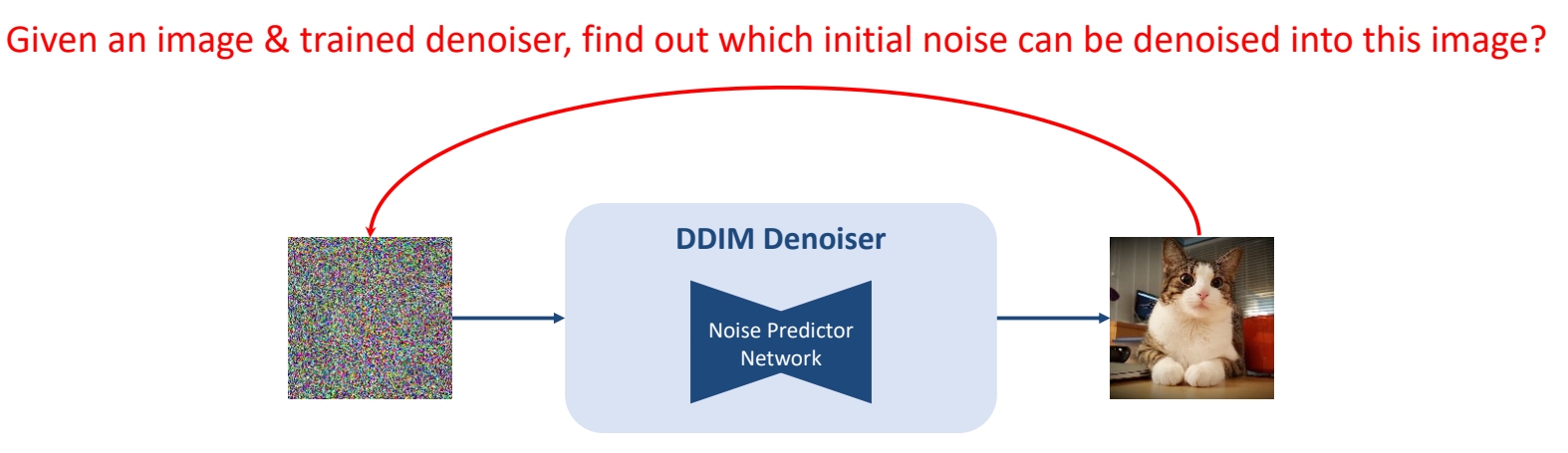
✅ 已有训好的 denoiser,输入干净图像,求它的噪声。
P17
前向过程与 DDIM Inverse 的区别
Forward Diffusion Process: Add \(\mathcal{N} (0,\mathbf{I} ) \) Noise
DDIM Inversion Process: Add Noise inverted by the trained DDIM denoiser
DDIM Inverse的应用
-
DDIM Inverse 可用于图片编辑
-
\(x_T\)可以是生成图片的隐空间编码,且它具备其它隐概率模型(如GAN[2])所观察到的语义插值效应。

Su et al., “Dual Diffusion Implicit Bridges for Image-to-Image Translation,” ICLR 2023.
Mokadi et al., “Null-text Inversion for Editing Real Images using Guided Diffusion Models,” CVPR 2023.
遗留问题
不按推理步骤按序预测噪声会不会有问题。
答案是不会。
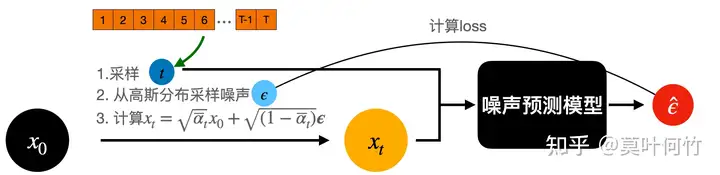
从上图可以看到,在训练时,是从时间序列\([1,2,\dots,T]\)进行采样时间步,再从高斯分布采样噪声,直接从\(x_0\) 出发计算\(x_t\) ,随后传入模型,根据预测噪声与实际噪声计算损失迭代模型。我们可以看到在这个训练pipeline中并没有限制时序信息。当噪声预测模型充分训练时DDIM的采样序列 也是在训练过程中被充分训练的。(论文附录C.1给出了更为详尽的解释推导,感兴趣的同学可以看论文)。
缺陷
验证方法
参考材料
[1] https://zhuanlan.zhihu.com/p/639540034
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/ReadPapers/